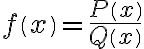Resum de funcions I

lloc:	Cursos IOC - Batxillerat
Curs:	Matemàtiques aplicades a les C. socials I (Bloc 1) ~ gener 2020
Llibre:	Resum de funcions I

Imprès per:	Usuari convidat
Data:	diumenge, 5 de maig 2024, 08:58

Descripció

Primers conceptes de funcions.

El concepte de funció

En contextos quotidians i científics ens trobem molt sovint amb la relació de variables: l'espai que recorre una partícula depèn del temps, la pressió de l'aigua del mar depèn de la profunditat, el preu que paguem per una carrera amb taxi depèn dels km recorreguts, ...

Anomenem funció a una relació de dependència entre dues magnituds, de manera que a cada valor de la primera magnitud li correspon un únic valor de la segona.

La segona variable depèn del valor de la primera i d'aquí que la primera s'anomena variable independent i la segona variable dependent.

Hi ha moltes maneres d'expressar una funció, per exemple:

- - Mitjançant un enunciat
  - Mitjançant una taula
  - Mitjançant un gràfic
  - Mitjançant una expressió algebraica o fórmula

Imatges i antiimatges

Quan tenim una funció i un nombre x es relaciona amb un altre nombre y ho expressem dient y=f(x)

Això ho llegiríem dient que y és la imatge de x per la funció f i també que x és una antiimatge de y per la funció f.

En cas de conèixer l'expressió algebraica de la funció:

Si volem calcular una imatge, f(a), coneixem la x i hem de trobar la y. Haurem de substituir la x per a a l'expressió de la funció i fer els càlculs. Tots els valors del domini tenen una i només una imatge.
Si volem calcular una antiimatge f^-1(b), coneixem la y i volem calcular la x. En aquest cas igualarem l'expressió algebraica a b i aïllarem la x, és a dir caldrà resoldre una equació. Pot ser que un valor no tingui antiimatge o en tingui més d'una.

Exemples

Donada la funció :

f parèntesi esquerre x parèntesi dret igual fracció numerador x al quadrat menys 1 entre denominador x més 2 fi fracció

Calculem algunes imatges i antiimatges

Imatge de 2

$f parèntesi esquerre 2 parèntesi dret igual fracció numerador 2 al quadrat menys 1 entre denominador 2 més 2 fi fracció igual fracció numerador 4 menys 1 entre denominador 4 fi fracció igual fracció 3 entre 4$

La imatge de 2 per la funció f és 3/4, i per tant la funció passa pel punt (2, 3/4).

I podem dir que la antiimatge de 3/4 és 2.

Antiimatge de 0

Per calcular la antiimatge de 0 per f, igualarem a 0 l'expressió i aïllarem la x.

$fracció numerador x al quadrat menys 1 entre denominador x més 2 fi fracció igual 0$

Una fracció és 0, si ho és el numerador:

$x al quadrat menys 1 igual 0 per parèntesi esquerre x més 2 parèntesi dret x al quadrat menys 1 igual 0 espai espai espai espai espai espai x al quadrat igual 1 espai espai espai espai espai espai x igual més-menys arrel quadrada de 1 espai espai espai espai espai negreta espai bold italic x negreta igual negreta més-menys negreta 1 espai$

Per tant, el 0 té dues antiimatges: 1 i -1

$f parèntesi esquerre 1 parèntesi dret igual 0 espai espai espai espai espai espai espai i espai espai espai espai espai espai f parèntesi esquerre menys 1 parèntesi dret igual 0 espai$

i la funció passa pels punts (1,0) i (-1,0)

Antiimatge de -8

$fracció numerador x al quadrat menys 1 entre denominador x més 2 fi fracció igual menys 8 x al quadrat menys 1 igual menys 8 per parèntesi esquerre x més 2 parèntesi dret x al quadrat menys 1 igual menys 8 x menys 16 x al quadrat més 8 x més 15 igual 0 x igual fracció numerador menys 8 més-menys arrel quadrada de 8 al quadrat menys 4 per 15 fi arrel entre denominador 2 fi fracció igual fracció numerador menys 8 més-menys arrel quadrada de 64 menys 60 fi arrel entre denominador 2 fi fracció igual fracció numerador menys 8 més-menys arrel quadrada de 4 entre denominador 2 fi fracció igual fracció numerador menys 8 més-menys 2 entre denominador 2 fi fracció igual taula fila cel·la punts suspensius inclinats cap amunt espai fracció numerador menys 10 entre denominador 2 fi fracció igual menys 5 fi cel·la fila cel·la punts suspensius inclinats cap avall fracció numerador menys 6 entre denominador 2 fi fracció igual menys 3 fi cel·la fi taula$

Per tant, -8 té dues antiimatges: -5 i 3

f parèntesi esquerre menys 5 parèntesi dret igual menys 8 espai espai espai espai espai espai espai i espai espai espai espai espai espai f parèntesi esquerre menys 3 parèntesi dret igual menys 8 espai

Es recomana llegir amb atenció el document " El concepte de funció" on trobareu explicacions i exemples senzills dels primers conceptes de funcions: càlcul d'imatges i antiimatges.

Interpretació d'una gràfica

Tal com hem dit, una de les formes d'expressar una funció és a partir d'una gràfica. Una gràfica ens dona una informació gràfica i visual entre dues magnituds que depenen una de l'altre.

La variable independent es representa sobre l'eix horitzontal (o d'abscisses) i la variable dependent sobre l'eix vertical (ordenades).

És important saber interpretar els gràfics perquè ens en trobem en tots els mitjans de comunicació cada dia.

Veiem un exemples d'un tema d'actualitat.

Exemple

El sector del transport és el responsable d'una part important de les emissions de CO2 a l'atmosfera. Aquest gràfic es visualitzen l'extracció de petroli en milions de barrils, i també el consum, al llarg d'una sèrie d'anys.

Després d'observar el gràfic, responeu:

a) Durant l'any 2000, quina va ser aproximadament l'extracció en milions de barrils?

b) En aquest any quin va se el consum?.

c) En quin any es va produir l'extracció mínima?

d) En quin moment la diferència entre l'extracció i el consum va ser mínima? I màxima?

Solucions

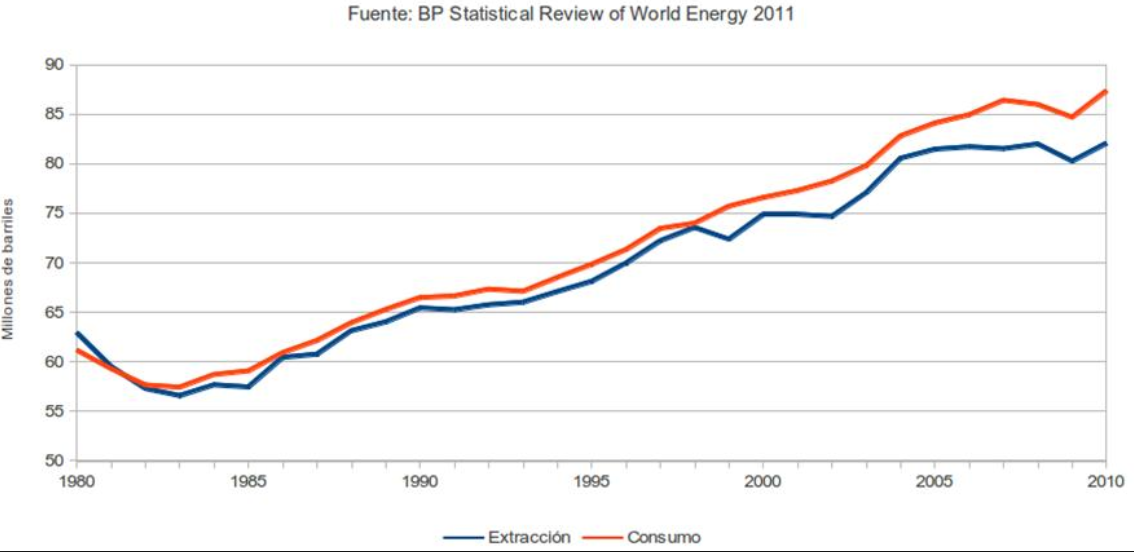
a) Observant la gràfica de color blau, que correspon a "extracció", la imatge de x=2000 és y=75 milions de barrils, per tant l'exptracció a l'any 2000 va ser aproximadament d'uns 75 milions de barrils.

b) Observant la gràfica de color vermell, que correspon a "consum" , veiem que és aproximadament es van consumir 77 milions de barrils l'any 2000.

c) Observant la gràfica de color blau, que correspon a "extracció" l'any amb menor nombre de barrils extrets és l'any 1983.

d) La menor diferència entre les dues gràfiques correspon a l'any 1981 i en 1998, on la diferència va ser de zero (observem que en aquests anys els gràfics es tallen. I la màxima a l'any 2009 en el qual es van consumir 5 milions de barrils més que els que es van extraure.

Domini i recorregut

Domini

El domini d'una funció f el formen els valors de la variable independent x que tenen imatge per f. Els representem per Dom f. És a dir, són els punts on té sentit definir la funció.

Els dominis s'expressen de diferents formes segons convingui: com a conjunt de punts i com a intervals de la recta real. És important que en aquest punt repasseu els intervals que es van treballar en el primer lliurament.

Què s'ha de tenir en compte en calcular el domini d'una funció?

Si tenim una funció definida de forma algebraica, és a dir com una fórmula, per calcular el seu domini haurem de trobar els valors reals on té sentit aplicar l'expressió algebraica, en aquest cas serà important saber treballar amb equacions i inequacions. Bàsicament caldrà vigilar:

Si la funció és polinòmica el domini estarà format per tots els nombres reals ( $normal nombres reals$ ) .
Si la funció és racional, és a dir és quocient de dos polinomis: $f parèntesi esquerre x parèntesi dret igual fracció numerador P parèntesi esquerre x parèntesi dret entre denominador Q parèntesi esquerre x parèntesi dret fi fracció$ , el domini seran tots els valors reals excepte aquells que anul·len el denominador (ja sabem que si dividim per 0 dóna infinit), per això: $D o m espai f igual normal nombres reals menys clau esquerra x barra vertical Q parèntesi esquerre x parèntesi dret igual 0 clau dreta$
Si la funció té arrels amb índex parell $f parèntesi esquerre x parèntesi dret igual arrel amb índex 2 n de g parèntesi esquerre x parèntesi dret fi arrel$ , sabem que no està definides en els negatius, per tant caldrà trobar quins valors fan que el radicand sigui negatiu i treure'ls del domini. $D o m espai f parèntesi esquerre x parèntesi dret igual clau esquerra x espai barra vertical espai g parèntesi esquerre x parèntesi dret major o igual que 0 clau dreta$
Si la funció té una arrel amb índex senar, $f parèntesi esquerre x parèntesi dret igual arrel amb índex 2 n més 1 de g parèntesi esquerre x parèntesi dret fi arrel$ no té cap problema de definició. Per tant $D o m espai f espai igual espai normal nombres reals$ .
Si la funció és logarítmica (les treballarem més endavant) $f parèntesi esquerre x parèntesi dret igual log subíndex a parèntesi esquerre g parèntesi esquerre x parèntesi dret parèntesi dret$ , només es podran aplicar a valors positius $D o m espai f parèntesi esquerre x parèntesi dret igual clau esquerra x espai barra vertical espai g parèntesi esquerre x parèntesi dret major que 0 clau dreta$
Per trobar el domini de funcions definides a trossos haurem de calcular el domini de cadascun dels trossos i unir-los. Cal tenir en compte en quina regió està definida cada tros.
Si treballem amb una funció en un context, caldrà imposar també que tingui sentit la funció dins del context.

Si el que tenim és el gràfic de la funció, trobar-ne el domini passarà per trobar els punts de l'eix horitzontal que tenen imatge, és a dir x=a pertany al domini de la funció si la recta vertical x=a talla al gràfic en un punt.

En aquest document, trobareu exemples resolts pas a pas del càlcul de dominis de diferents tipus de funcions, no deixeu de consultar-lo.(Només la part de dominis de polinomis i funcions racionals)

Recorregut

El recorregut o rang d'una funció f és el conjunt format per totes les imatges de f, és a dir són tots els valors y que són imatge d'alguna x.

El denotem $bold italic I bold italic m negreta espai bold italic f$

Gràficament la imatge o recorregut de f la formen tots els valors verticals del gràfic.

Exemples

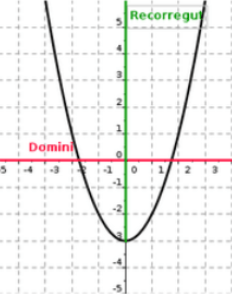
A l'esquerra tenim el gràfic d'una funció f(x)=x²-3

En tractar-se d'una funció polinòmica el domini està format per tots els nombres reals, és a dir: Dom f= R

Per altra banda observant el gràfic per trobar el recorregut veiem que verticalment pren valors entre -3 i fins a infinit (les branques seguirien creixent, tot i que aquí només en posem un tros), per tant Im f = [-3, +∞)

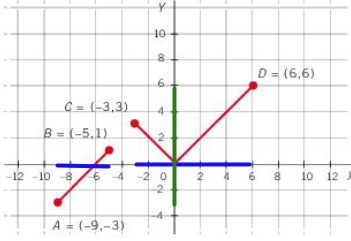
A l'esquerra tenim el gràfic d'una funció a trossos.

Per trobar-ne el domini cal veure quins valors de l'eix horitzontal tenen imatge, hem assenyalat en color blau els punts que ho compleixen: Dom f= [-9,-5] U [-3,6]

Per altra banda observant el gràfic per trobar el recorregut veiem que verticalment pren valors entre -3 i fins a 6, per tant Im f = [-3, 6]

Exemples de càlcul de dominis

a) $bold italic f negreta parèntesi esquerre bold italic x negreta parèntesi dret negreta igual negreta 342 negreta espai negreta més negreta 39 negreta espai bold italic x negreta menys negreta 3 bold italic x negreta ²$

f(x) és una funció polinòmica i per tant $D o m espai f parèntesi esquerre x parèntesi dret igual negreta nombres reals$ (tots els nombres reals).

b) $espai bold italic f negreta parèntesi esquerre bold italic x negreta parèntesi dret negreta igual fracció negreta 1 entre negreta x espai espai espai$

El denominador és x

El denominador s'anul·la en x=0

$D subíndex f igual negreta nombres reals negreta menys obre claus negreta 0 tanca claus$

c) $negreta espai negreta espai bold italic f negreta parèntesi esquerre bold italic x negreta parèntesi dret negreta igual fracció numerador negreta x negreta menys negreta 2 entre denominador negreta x negreta més negreta 3 fi fracció negreta espai espai espai$

El denominador s'anul·la en:

$x més 3 igual 0 espai espai espai espai espai x igual menys 3$

$D subíndex f igual negreta nombres reals negreta menys obre claus negreta menys negreta 3 tanca claus$

d) $negreta espai bold italic f negreta parèntesi esquerre bold italic x negreta parèntesi dret negreta igual fracció numerador negreta x entre denominador negreta x elevat a negreta 2 negreta menys negreta 25 fi fracció espai espai espai$

Mirem on s'anul·la el denominador:

$x al quadrat menys 25 igual 0 espai espai espai espai espai espai espai espai espai espai x al quadrat igual 25 espai espai espai espai espai espai espai espai x igual més-menys arrel quadrada de 25 igual més-menys 5$

$bold italic D subíndex negreta f negreta igual negreta nombres reals negreta menys obre claus negreta més-menys negreta 5 tanca claus$

e) $espai bold italic f negreta parèntesi esquerre bold italic x negreta parèntesi dret negreta igual fracció numerador negreta x elevat a negreta 2 entre denominador negreta x elevat a negreta 2 negreta menys negreta 3 negreta x fi fracció negreta espai negreta espai negreta espai$

Mirem on s'anul·la el denominador:

$x al quadrat menys 3 x igual 0 x per parèntesi esquerre x menys 3 parèntesi dret igual 0 espai espai fletxa doble dreta obre claus taula fila cel·la x igual 0 espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai fi cel·la fila cel·la espai espai espai espai espai espai espai espai espai espai espai espai espai fi cel·la fila cel·la x menys 3 igual 0 espai espai fletxa dreta x igual 3 fi cel·la fi taula tanca espai espai espai espai$

$D subíndex f igual negreta nombres reals negreta menys obre claus negreta 0 negreta coma negreta 3 tanca claus$

$negreta f negreta parèntesi dret espai espai f parèntesi esquerre x parèntesi dret igual fracció numerador x entre denominador x al quadrat més 1 fi fracció espai espai espai espai espai espai espai espai espai espai espai espai x al quadrat més 1 igual 0 espai espai espai espai espai espai espai espai espai x al quadrat igual menys 1 espai espai espai Aquesta espai equació espai no espai té espai solució espai espai espai espai espai espai espai bold italic D subíndex negreta f negreta igual negreta nombres reals$

g) $g parèntesi esquerre x parèntesi dret igual fracció numerador x ² entre denominador x ² més 2 x menys 3 fi fracció$

g(x) és una funció racional. Domini de la funció = R-{valors que anul·len el denominador}

Calculem doncs els valor s que anul·len el denominador:

$x ² més 2 x menys 3 igual 0 x igual fracció numerador menys 2 més-menys arrel quadrada de 4 menys 4 per 1 per parèntesi esquerre menys 3 parèntesi dret fi arrel entre denominador 2 per 1 fi fracció igual fracció numerador menys 2 més-menys arrel quadrada de 16 entre denominador 2 fi fracció igual fracció numerador menys 2 més-menys 4 entre denominador 2 fi fracció x subíndex 1 igual 1 x subíndex 2 igual menys 3$

Per tant: $D subíndex g igual normal nombres reals menys obre claus menys 3 coma 1 tanca claus$

h) $h parèntesi esquerre x parèntesi dret igual arrel quadrada de 2 x menys 5 fi arrel$

h(x) és una funció irracional d'índex parell, ja que l'arrel és quadrada.

Domini de la funció = {valors de "x" que fan que el radicand ≥ 0} Cal resoldre la inequació:

$2 x menys 5 major o igual que 0 2 x major o igual que 5 x major o igual que fracció 5 entre 2 x major o igual que 2.5 bold italic D bold italic o bold italic m negreta espai bold italic h negreta parèntesi esquerre bold italic x negreta parèntesi dret negreta espai negreta igual negreta espai negreta claudàtor esquerre negreta 2 negreta. negreta 5 negreta espai negreta coma negreta espai negreta més negreta infinit negreta parèntesi dret$

$negreta i negreta parèntesi dret espai espai f parèntesi esquerre x parèntesi dret igual arrel quadrada de x espai espai fletxa dreta espai espai espai D subíndex f igual claudàtor esquerre 0 coma més infinit parèntesi dret espai espai espai$ podríem posar també $D subíndex f igual normal nombres reals elevat a més$

$bold italic j negreta parèntesi dret espai espai f parèntesi esquerre x parèntesi dret igual arrel quadrada de menys x fi arrel espai espai fletxa dreta espai espai espai D subíndex f igual parèntesi esquerre menys infinit coma 0 claudàtor dret espai espai espai$ podríem posar també $D subíndex f igual normal nombres reals elevat a menys$

$bold italic k negreta parèntesi dret espai espai f parèntesi esquerre x parèntesi dret igual arrel quadrada de x menys 1 fi arrel espai espai fletxa dreta espai espai espai D subíndex f igual claudàtor esquerre 1 coma més infinit parèntesi dret espai espai espai$

$negreta l negreta parèntesi dret negreta espai espai f parèntesi esquerre x parèntesi dret igual arrel quadrada de x al quadrat més 1 fi arrel espai espai fletxa dreta espai espai espai D subíndex f igual normal nombres reals$

$negreta m negreta parèntesi dret espai espai f parèntesi esquerre x parèntesi dret igual arrel cúbica de x espai espai fletxa dreta espai espai espai D subíndex f igual normal nombres reals$

Exemples de càlcul de dominis

Aquí teniu més exemples de càlcul de dominis.

a) $f parèntesi esquerre x parèntesi dret igual fracció 4 entre x$

Observem que per a x=0 queda

estil mida 14px f parèntesi esquerre 0 parèntesi dret igual fracció 4 entre 0 fi estil

Però 4/0 no és cap nombre real (podeu provar de posar en la calculador 4/0 i veure que us dona).
Per a qualsevol altre valor de x diferent de 0, podem fer el quocient i per tant existirà imatge per a aquest valor de x,

Per tant, el domini és tots els nombres reals excepte el 0. Ho expressem així:

bold italic D negreta igual negreta nombres reals negreta menys obre claus negreta 0 tanca claus

b) $f parèntesi esquerre x parèntesi dret igual fracció numerador x més 2 entre denominador parèntesi esquerre x menys 2 parèntesi dret per parèntesi esquerre x més 3 parèntesi dret fi fracció$

f(x) és una funció racional, el domini serà tots els nombres excepte els que anul·len el dominador.
Trobem les solucions de l'equació (x-2)·(x+3)=0.

Tingueu en compte que perquè un producte sigui 0, ha de ser 0 un dels seus factors.

parèntesi esquerre x menys 2 parèntesi dret per parèntesi esquerre x més 3 parèntesi dret igual 0 espai espai espai espai fletxa doble dreta espai espai taula fila cel·la punts suspensius inclinats cap amunt espai espai x menys 2 igual 0 espai espai fletxa dreta espai x igual 2 fi cel·la fila cel·la punts suspensius inclinats cap avall espai x més 3 igual 0 espai espai fletxa dreta x igual menys 3 fi cel·la fi taula

Per tant,

bold italic D negreta igual negreta nombres reals negreta menys obre claus negreta menys negreta 3 negreta coma negreta 2 tanca claus

c) $f parèntesi esquerre x parèntesi dret igual espai arrel cinquena de fracció numerador x més 1 entre denominador x menys 2 fi fracció fi arrel$

Com que l'índex n del radical és imparell, sempre es possible trobar la imatge de qualsevol nombre real (sigui positiu o negatiu).

Només hem de tenir en compte que sigui del domini de 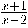$\frac{x+1}{x-2}$

Per tant,

bold italic D negreta igual negreta nombres reals negreta menys obre claus negreta 2 tanca claus

f parèntesi esquerre x parèntesi dret igual arrel quadrada de fracció numerador 4 entre denominador x menys 5 fi fracció fi arrel

Com que l'índex n del radical és parell, cal que el radicant sigui més gran o igual que 0.
Per tant el domini de f, és el conjunt solució de la inequació

x menys 5 major o igual que 0

x menys 5 major o igual que 0 espai espai espai fletxa dreta espai x major o igual que 5

Expressat en forma d'interval:

bold italic D negreta igual negreta claudàtor esquerre negreta 5 negreta coma negreta més negreta infinit negreta parèntesi dret

Punts de tall amb els eixos

A l'hora de fer un gràfic, hi ha diverses característiques que ens ajuden a dibuixar-lo, entre elles els talls amb els eixos.

Els punts de tall amb els eixos, són aquells punts on el gràfic de la funció talla amb els eixos de coordenades.

Punts de tall amb l'eix d'abscisses (de les x)

Seran punts de tipus (a,0). Per calcular-los igualarem la funció a 0 i en buscarem les possibles solucions (si n'hi ha) de l'equació que en resulta.

Pot haver-n'hi o no i també pot haver-n'hi més d'un.

Exemple

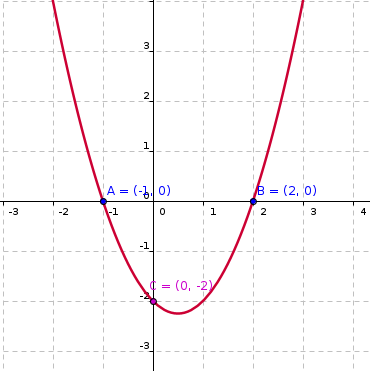
Donada la funció f(x)= x² - x - 2 , per trobar els seus punts de tall amb l'eix de les x, farem:

x² -x - 2 = 0 -----> x= -1 i x= 2

Per tant la funció talla a l'eix d'abscisses en dos punts A=(-1, 0) i B=(2, 0)

Punts de tall amb l'eix d'ordenades (de les y)

Seran punts de tipus (0,b). Per calcular-los només cal calcular la imatge del 0 (sempre que el 0 sigui del domini de la funció). Una funció només pot tallar l'eix vertical en un sol punt, perquè si 0 pertany al domini de f, per definició de funció cada punt té una única imatge.

Exemple

Seguint amb la funció anterior, la imatge del 0 serà f(0)= 0- 0 -2= -2

Per tant el punt de tall és C=(0, -2)

Monotonia i extrems

Una funció monòtona és creixent o decreixent.

Una funció és creixent en un interval, si sempre que x₁ < x₂→f( x₁ ) $menor o igual que$ f( x₂). És a dir si augmentem el valor de les x, augmenten també les imatges. Observem que les imatges poden ser més grans o iguals.

Una funció és estrictament creixent en un interval si sempre que x₁ < x₂→f( x₁ )<f( x₂).
Una funció és decreixent en un interval si sempre que x₁ < x₂→f( x₁ ) $major o igual que$ f( x₂). És a dir en augmentar el valor de les x, el valor de les imatges disminueix. Observem que les imatges poden ser més petites o iguals.
Una funció és estrictament decreixent en un interval si sempre que x₁ < x₂→f( x₁ )> f( x₂). És a dir en augmentar el valor de les x, el valor de les imatges disminueix de forma estricta.

Màxims i mínims

L'estudi de la monotonia d'una funció portarà a trobar els possibles màxims i mínims.

Una funció té un màxim relatiu en un punt a, si en un entorn d'aquest punt les imatges són totes més petites o iguals que f(a). Això matemàticament ho escriurem : f(a) $major o igual que$ f(x) per a tot x de l'entorn de a.

Una funció té un mínim relatiu en un punt a, si en un entorn d'aquest punt les imatges són totes més grans o iguals que f(a). Això matemàticament ho escriurem : f(a) $menor o igual que$ f(x) per a tot x de l'entorn de a.

Observa en aquesta imatge que si tenim un màxim relatiu en el punt (a, f(a)) la funció creix a l'esquerra de a i decreix a la seva dreta. Si el que tenim és un mínim relatiu, passa el contrari: la funció a l'esquerra del punt ve decreixent i després passa a créixer.

Funcions polinòmiques de grau 1. Rectes.

Les funcions que tenen per gràfica una recta són de tipus f(x)=y=mx+n , per tant són funcions polinòmiques de grau 1. Aquestes funcions es diuen funcions afins.

El Domf= R i el recorregut també, és a dir Imf=R.

La m és el pendent de la recta i ens indica la inclinació d'aquesta i la velocitat de creixement.

Si la m≥0 la recta és creixent

Si la m≤0 la recta és decreixent

La n es diu ordenada a l'origen i ens indica el punt de tall de la recta amb l'eix vertical (de les y)

En el cas que la n=0 , la recta té equació f(x)=y=mx , aquestes funcions es diuen funcions lineals i tenen la peculiaritat que passen totes elles per l'origen de coordenades. Aquest tipus de funcions, que constitueixen un cas particular de funcions afins modelitzen les situacions de proporcionalitat directa que sorgeixen molt sovint a la vida quotidiana.

Un altre cas particular de funció afí es dona si la m=0. La funció queda de tipus f(x)=y=n i en aquest cas la funció és constant, sempre val el mateix, no depèn de x i el seu gràfic és horitzontal.

Si coneixem l'expressió d'aquestes funcions per dibuixar-ne el gràfic farem una taula de valors (tot i que amb 2 en tenim prou millor fer-ne 3 o 4 per garantir que no ens hem equivocat). Situem els punts als eixos coordenats i els unim formant una recta.

Exemple

y=3x+1		y=–2x		y= 3
x	y	x	y	x	y
-2	-5	-2	4	-2	3
-1	-2	-1	2	-1	3
0	1	0	0	0	3
1	4	1	-2	1	3
2	7	2	-4	2	3

Es recomana llegir atentament el document:

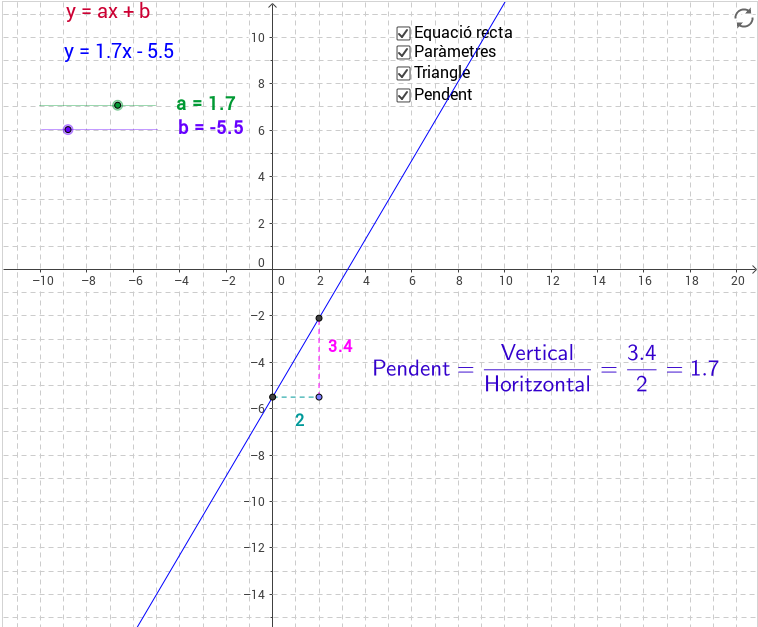
Funció que té per gràfica una recta

Cliqueu després damunt d'aquesta imatge per accedir a un applet fet amb Geogebra per Pep Bujosa. En moure els punts lliscants a i b podreu explorar com varia la gràfica de la recta en fer variar el pendent i l'ordenada a l'origen. Quines conclusions traieu després d'aquest estudi?

Funcions quadràtiques. Paràboles.

L'expressió algebraica d'una funció quadràtica és un polinomi de grau 2:

$bold italic f negreta parèntesi esquerre bold italic x negreta parèntesi dret negreta igual bold italic a bold italic x elevat a negreta 2 negreta més bold italic b bold italic x negreta més bold italic c$ amb a≠ 0

Com totes les funcions polinòmiques el dom està format per tots els nombres reals R

La gràfica és una paràbola.

Gràfica d'una paràbola

Per fer el gràfic d'una paràbola trobem els seus punts més significatius:

- Talls amb l'eix x La paràbola talla a l'eix x en les solucions de l'equació $a x al quadrat més b x més c igual 0$

- Tall amb l'eix y (0,f(0))

- Vèrtex La coordenada x del vèrtex és $x igual menys fracció numerador b entre denominador 2 a fi fracció$

Per trobar la coordenada y, substituïm aquest valor de x en ax²+bx+c

Vèrtex $obre parèntesis menys fracció numerador b entre denominador 2 a fi fracció coma espai f obre parèntesis menys fracció numerador b entre denominador 2 a fi fracció tanca parèntesis tanca parèntesis$

- Si $a major que 0 espai espai fletxa doble dreta$ la paràbola "mira" cap amunt

Si $a menor que 0 espai espai fletxa doble dreta$ la paràbola "mira" cap avall

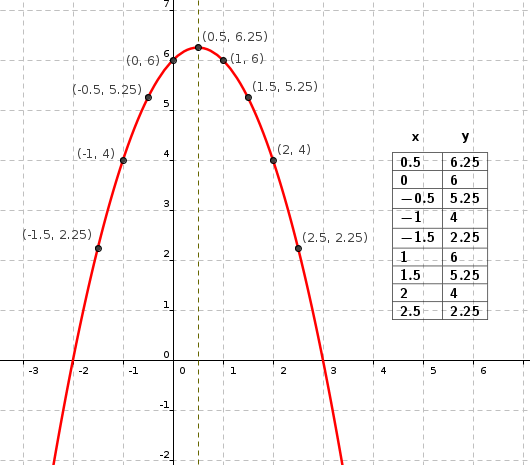
Exemple de paràbola 1

Considerem la funció

f parèntesi esquerre x parèntesi dret igual menys x ² més x més 6

, és un polinomi de grau 2.

Sabem que el seu gràfic serà una paràbola.

Pot ser convenient seguir aquest ordre d'estudi, l'expliquem pas a pas:

Pensar en la forma de la paràbola segons el signe del coeficient de grau dos: en aquest cas, en ser negatiu tindrà forma de campana, les branques baixen.

Trobar-ne el vèrtex: el vèrtex estarà en el punt d'abscissa $x igual fracció numerador menys b entre denominador 2 a fi fracció igual fracció numerador menys 1 entre denominador menys 2 fi fracció igual 1 mig$ , la seva imatge serà $f parèntesi esquerre 1 mig parèntesi dret igual menys parèntesi esquerre 1 mig parèntesi dret ² més 1 mig més 6 igual fracció numerador menys 1 entre denominador 4 fi fracció més 1 mig més 6 igual fracció numerador menys 1 més 2 més 24 entre denominador 4 fi fracció igual fracció 25 entre 4 igual 6.25$
Per tant el vèrtex serà el punt (0.5, 6.25)

Convé trobar els punts de tall amb els eixos i situar-los en el gràfic per tal de fer un dibuix més acurat.

-El tall amb l'eix d'ordenades el trobem quan x=0, (0, f(0))=(0,6)
-Els possibles talls amb l'eix d'abscisses els trobem en igualar a 0 la funció i trobar-ne les solucions.
Si resolem en aquest cas

f parèntesi esquerre x parèntesi dret igual menys x ² més x més 6 igual 0 espai menys menys menys major que x igual menys 2 espai i espai x igual 3

, per tant la paràbola talla a l'eix horitzontal en els punts (-2 , 0) i (3 , 0)

Fem una taula de valors: donem uns quants valors a la x i en busquem la imatge (la y). Convé que els valors de la x estiguin a les dues bandes de l'abscissa del vèrtex (0.5) perquè el gràfic serà simètric respecte a aquest eix.
Un cop tenim totes aquests punts els unim formant el gràfic.

En aquest document La funció quadràtica simple, trobareu més explicacions detallades sobre les paràboles amb vèrtex l'origen de coordenades.

Clicant damunt la següent imatge i accedireu a un applet fet amb geogebra (Autor: Francesc) que us permetrà explorar com canvia el gràfic de la funció quadràtica en variar-ne els seus coeficients. Traieu-ne conclusions.

Exemple de paràbola 2

Un altre exemple de gràfic de paràbola.

$bold italic f negreta parèntesi esquerre bold italic x negreta parèntesi dret negreta igual bold italic x elevat a negreta 2 negreta menys negreta 3 bold italic x negreta menys negreta 4$

Talls amb l'eix x

$x al quadrat menys 3 x menys 4 igual 0 espai x igual fracció numerador menys parèntesi esquerre menys 3 parèntesi dret més-menys arrel quadrada de parèntesi esquerre menys 3 parèntesi dret al quadrat menys 4 per 1 per parèntesi esquerre menys 4 parèntesi dret fi arrel entre denominador 2 per 1 fi fracció igual fracció numerador 3 més-menys arrel quadrada de 9 més 16 fi arrel entre denominador 2 fi fracció igual fracció numerador 3 més-menys 5 entre denominador 2 fi fracció igual obre claus taula atributs alineació columna left fin atributs fila cel·la fracció 8 entre 2 igual 4 fi cel·la fila cel·la fracció numerador menys 2 entre denominador 2 fi fracció igual menys 1 fi cel·la fi taula tanca$

Talls amb l'eix x: $negreta parèntesi esquerre negreta 4 negreta coma negreta 0 negreta parèntesi dret negreta coma negreta espai negreta parèntesi esquerre negreta menys negreta 1 negreta coma negreta 0 negreta parèntesi dret negreta espai$

Tall amb l'eix y

$f parèntesi esquerre 0 parèntesi dret igual 0 al quadrat menys 3 per 0 menys 4 igual menys 4$

Tall amb l'eix y: $negreta parèntesi esquerre negreta 0 negreta coma negreta menys negreta 4 negreta parèntesi dret$

Vèrtex

$x igual menys fracció numerador b entre denominador 2 a fi fracció igual menys fracció numerador menys 3 entre denominador 2 per 1 fi fracció igual fracció 3 entre 2$

$y igual f obre parèntesis fracció 3 entre 2 tanca parèntesis igual obre parèntesis fracció 3 entre 2 tanca parèntesis al quadrat menys 3 per fracció 3 entre 2 menys 4 igual fracció 9 entre 4 menys fracció 9 entre 2 menys 4 igual menys fracció 25 entre 4$

Per calcular la coordenada y del vèrtex substituïm en la funció:

Vèrtex $obre parèntesis fracció negreta 3 entre negreta 2 negreta coma negreta menys fracció negreta 25 entre negreta 4 tanca parèntesis$

Taula de valors

Per ajustar millor els punts, convé fer una taula amb uns quants valors (que es recomana que estiguin situats a banda i banda del vèrtex)

Gràfica

Recordeu:

Si el coeficient de la x²és positiu $fletxa doble dreta$ la paràbola "mira" cap amunt

Si el coeficient de la x²és negatiu $fletxa doble dreta$ la paràbola "mira" cap avall

Exemple de paràbola 3

Gràfic de la paràbola $bold italic f negreta parèntesi esquerre bold italic x negreta parèntesi dret negreta igual negreta menys bold italic x elevat a negreta 2 negreta més negreta 3 bold italic x$

Talls amb l'eix x

$menys x al quadrat més 3 x igual 0$

Per resoldre aquesta equació de segon grau incompleta no apliquem la fórmula de l'equació de segon grau

Ho fem més senzill extraient factor comú x:

$x per parèntesi esquerre menys x més 3 parèntesi dret igual 0 espai espai espai espai fletxa doble dreta espai espai espai x igual 0 espai espai espai o espai espai espai menys x més 3 igual 0 espai espai espai espai espai fletxa doble dreta espai espai x igual 0 espai espai espai espai espai o espai espai espai espai espai x igual 3$

Talls amb l'eix x:

negreta parèntesi esquerre negreta 0 negreta coma negreta 0 negreta parèntesi dret negreta coma negreta espai negreta parèntesi esquerre negreta 3 negreta coma negreta 0 negreta parèntesi dret negreta espai

Tall amb l'eix y

Calculem la imatge de 0: $f parèntesi esquerre 0 parèntesi dret igual menys 0 al quadrat més 3 per 0 igual 0$

Tall amb l'eix y: $negreta parèntesi esquerre negreta 0 negreta coma negreta 0 negreta parèntesi dret$

Vèrtex

Coordenada x del vèrtex

$x igual menys fracció numerador b entre denominador 2 a fi fracció igual menys fracció numerador menys 3 entre denominador 2 per parèntesi esquerre menys 1 parèntesi dret fi fracció igual fracció 3 entre 2$

Per calcular la coordenada y del vèrtex substituïm en la funció:

$y igual f obre parèntesis fracció 3 entre 2 tanca parèntesis igual menys obre parèntesis fracció 3 entre 2 tanca parèntesis al quadrat més 3 per fracció 3 entre 2 igual menys fracció 9 entre 4 més fracció 9 entre 2 igual fracció 9 entre 4$

Vèrtex $obre parèntesis fracció negreta 3 entre negreta 2 negreta coma fracció negreta 9 entre negreta 4 tanca parèntesis$

Gràfica

Recordem:

Si el coeficient de la x²és positiu $fletxa doble dreta$ la paràbola "mira" cap amunt

Si el coeficient de la x²és negatiu $fletxa doble dreta$ la paràbola "mira" cap avall

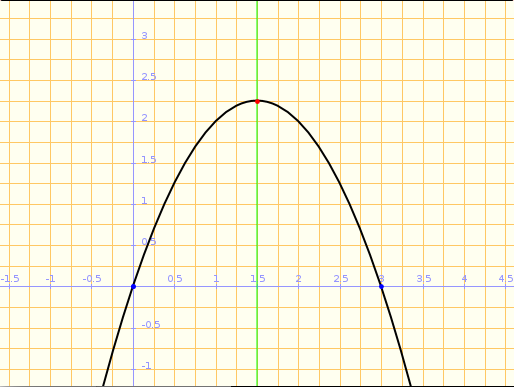
Problema

L'evolució de les accions d'una empresa, va seguir , durant l'any passat, aproximadament aquesta funció:

$bold italic f negreta parèntesi esquerre bold italic t negreta parèntesi dret negreta igual negreta menys negreta 30 bold italic t elevat a negreta 2 negreta més negreta 240 bold italic t negreta menys negreta 210$

essent t el temps en mesos (0≤t≤12) i f(t) la cotització de les accions en euros.

a) Dibuixeu la gràfica.

Com que es tracta d'una paràbola, trobem:

Talls amb l'eix x

En aquest problema, la variable independent s'anomena t en lloc de x, però tot es fa igual.

$menys 30 t al quadrat més 240 t menys 210 igual 0$

Tot i que no és necessari, podem dividir tota l'equació entre 30 per simplificar els càlculs.

$menys t al quadrat més 8 t menys 7 igual 0$

$estil mida 14px t igual fracció numerador menys 8 més-menys arrel quadrada de parèntesi esquerre menys 8 parèntesi dret al quadrat menys 4 per parèntesi esquerre menys 1 parèntesi dret per parèntesi esquerre menys 7 parèntesi dret fi arrel entre denominador 2 per parèntesi esquerre menys 1 parèntesi dret fi fracció igual fracció numerador menys 8 més-menys arrel quadrada de 64 menys 28 fi arrel entre denominador menys 2 fi fracció igual fracció numerador menys 8 més-menys arrel quadrada de 36 entre denominador menys 2 fi fracció igual espai espai espai espai espai espai fracció numerador menys 8 més-menys 6 entre denominador menys 2 fi fracció igual taula fila cel·la punts suspensius inclinats cap amunt fracció numerador menys 8 més 6 entre denominador menys 2 fi fracció igual fracció numerador menys 2 entre denominador menys 2 fi fracció igual 1 fi cel·la fila cel·la punts suspensius inclinats cap avall fracció numerador menys 8 menys 6 entre denominador menys 2 fi fracció igual fracció numerador menys 14 entre denominador menys 2 fi fracció igual 7 fi cel·la fi taula fi estil$

Punts de tall amb l'eix x: (1,0), (7,0)

Tall amb l'eix y

Calculem la imatge de 0

f(0)= -210

Punt de tall amb l'eix y: (0, -210)

Vèrtex

$estil mida 14px obre parèntesis fracció numerador menys b entre denominador 2 a fi fracció coma espai espai f obre parèntesis fracció numerador menys b entre denominador 2 a fi fracció tanca parèntesis tanca parèntesis fi estil$

$estil mida 14px x subíndex v igual fracció numerador menys b entre denominador 2 a fi fracció igual fracció numerador menys 240 entre denominador 2 per parèntesi esquerre menys 30 parèntesi dret fi fracció igual 4 y subíndex v igual menys 30 per parèntesi esquerre 4 parèntesi dret al quadrat espai més 240 per espai fi parèntesi esquerre 4 parèntesi dret espai menys 210 espai igual 270 fi estil$

V(4, 270)

b) En quin mes es va assolir la màxima cotització, i quina va ser aquesta cotització?

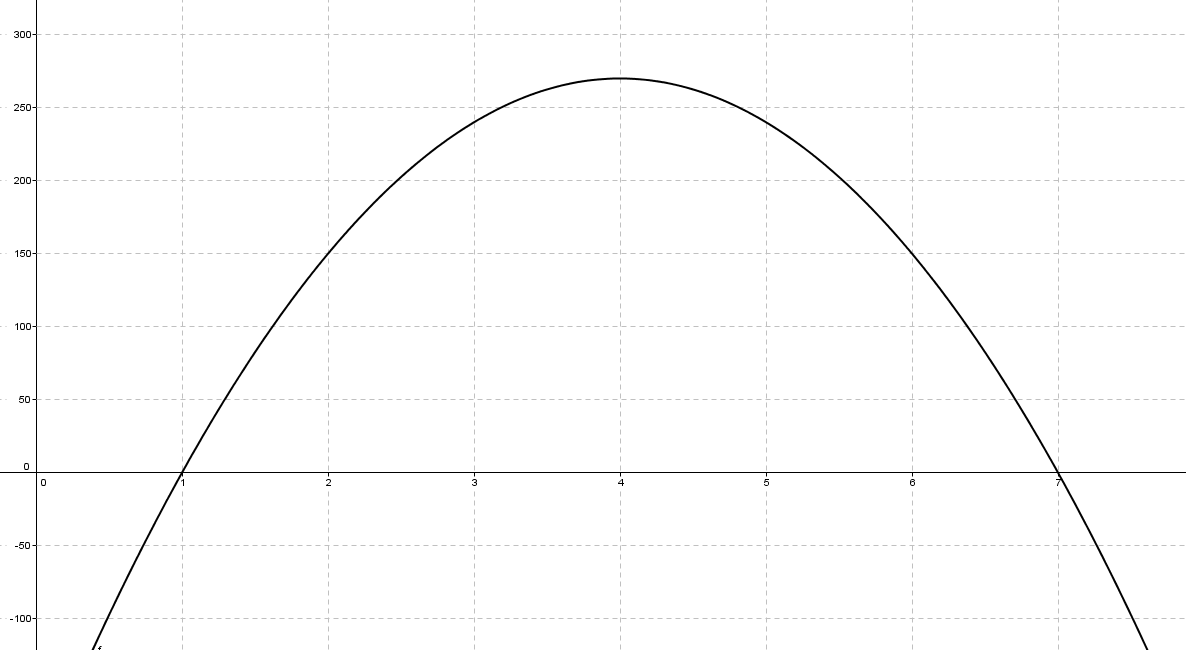
En funcions quadràtiques l'extrem (màxim o mínim) s'assoleix en el vèrtex de la paràbola.

En aquest cas, el màxim és el vèrtex de la paràbola, que ja ho hem trobat en l'apartat anterior.

Per tant: la màxima cotització s'assoleix en el mes 4 i és de 270 €.

Altres tipus de funcions

A banda dels polinomis de grau 1 (rectes) i els de grau 2 (paràboles) ens trobem amb molts tipus de funcions.

Segons la seva expressió algebraica en destaquen:

funcions polinòmiques de grau superior a 2
funcions racionals o algebraiques.
funcions irracionals
funcions exponencials
funcions logarítmiques
funcions trigonomètriques
funcions definides a trossos: valor absolut,...
....

En aquest curs només només treballarem alguns d'aquests tipus.

Funcions racionals

Són aquelles que tenen com a expressió algebraica el quocient de dos polinomis

$f\left(x\right)= \frac{P\left(x\right)}{Q\left(x\right)}$

El domini d'aquestes funcions està format per R–{x| Q(x)=0}

És a dir, el domini són tots els valors reals menys aquells que anul·len el denominador. Per calcular els zeros del polinomi del denominador et caldrà resoldre una equació.

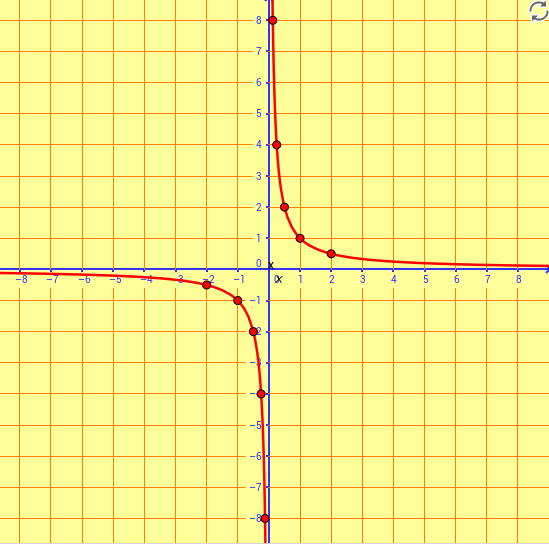
Un cas particular d'aquestes funcions són les funcions de proporcionalitat inversa $f (x) = \frac{k}{x}$ amb k una constant. La seva gràfica és una hipèrbola.

Cliqueu damunt la imatge i accedireu a un applet fet amb Geogebra per Juli Jurado de la funció de proporcionalitat inversa $f (x) = \frac{k}{x}$ podreu fer variar la k, des de -4 fins a 4. Què observeu?

Exemples

$f (x) = \frac{x ³ - x ² + 1}{x - 3}$ el domini seria en aquest cas R – {3} ja que x-3=0---->x=3

$g (x) = \frac{x ³ - x ² + 1}{x^{2} + 1}$ el domini seria tot R, perquè en aquest cas el denominador no s'anul·la mai. x²+1=0---->x²= -1 i això no té solució en el conjunt de nombres reals.
$h (x) = \frac{x ³ - x ² + 1}{x^{3} - x}$ el domini seria tot R – {-1, 0, 1}, perquè en aquest cas el denominador s'anul·la en aquests tres punts: $x ³ - x = x (x ² - 1) = x \cdot (x - 1) \cdot (x + 1)$

A la següent imatge pots veure els gràfics de les tres funcions anteriors. Observa en el dibuix que el domini calculat es correspon amb el que veiem al gràfic.

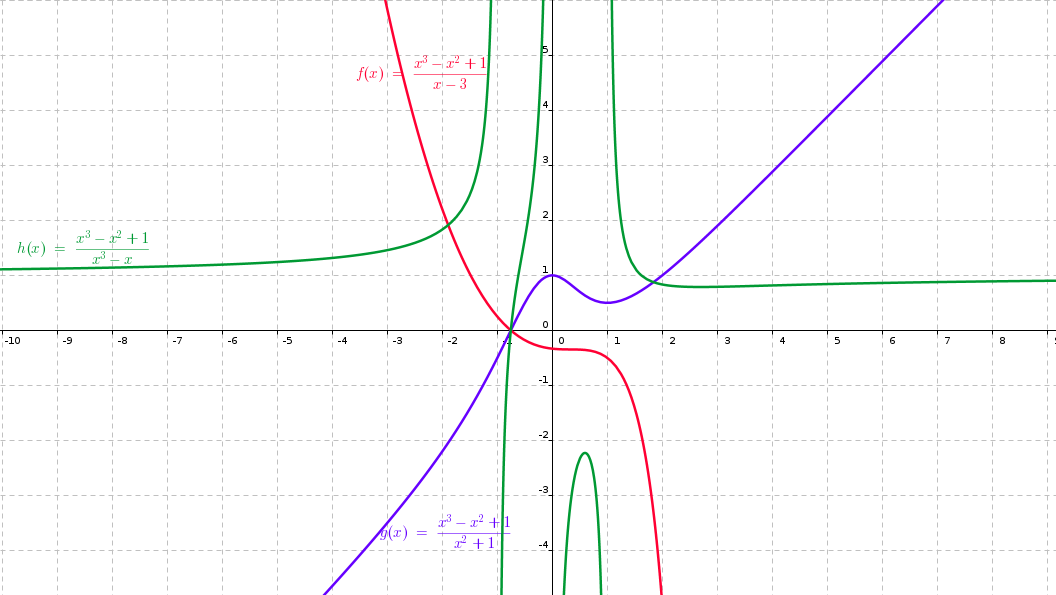
A partir dels gràfics, esbrina quina seria la Imatge o recorregut de cadascuna de les tres funcions?

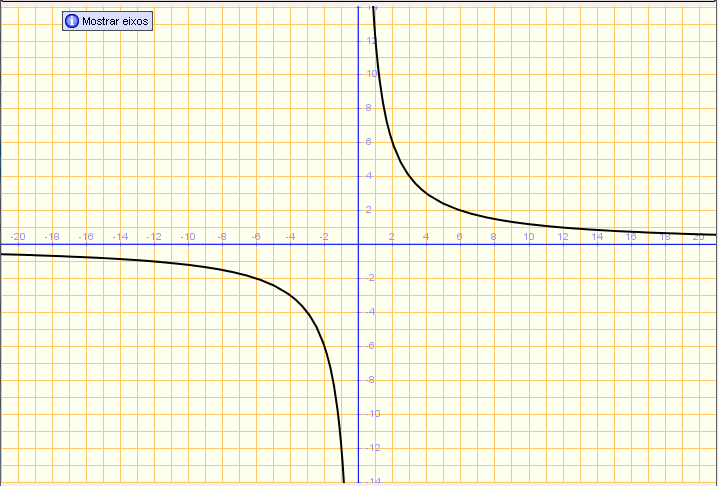
Funcions de proporcionalitat inversa. Hipèrboles

Una funció racional especialment important és la funció de proporcionalitat inversa, que té una expressió del tipus:

$y igual fracció k entre x o n espai k espai é s espai u n espai n o m b r e espai i espai k espai no igual espai 0$

El domini de la funció és Don f(x) = R-{0}

Té per gràfica una hipèrbola.

Veiem un exemple aplicat, d'aquest tipus de funcions.

Treball en equip

Un grup de noies i nois aficionats a la informàtica estan preparant la pàgina web d'una associació. Han calculat que treballant en grups de 3 necessiten 4 hores per enllestir una pàgina, tenint en compte que s'han de fer fotografies, redactar els textos i muntar la pàgina. El temps se'ls tira a sobre però tampoc volen ser una multitud. Per això fan una taula que relacioni el nombre de persones i les hores que els calen per fer una pàgina:

Nois/es	1	2	3	4	5	6	7	8	9	10	12
Hores	12	6	4	3	2.4	2	1,7	1,5	1,3	1,2	1

Si augmenta el nombre de persones del grup, disminueix el nombre d'hores, i si disminueix el nombre de persones, augmenta el nombre d'hores.

Observeu que el producte (multiplicació) del nombre de persones per les hores és sempre 12. Aquest nombre li diem constant de proporcionalitat inversa i es refereix a la k.

Si anomenem x =nombre de persones i y= hores, la relació s'expressa de la forma

$y igual fracció 12 entre x$

Es diu que les dues magnituds són inversament proporcionals.

En aquest cas concret la funció només té sentit per valors sencers i positius de x, perquè x representa el nombre de persones.

Funcions definides a trossos

En una funció a trossos hi ha diferents expressions segons l'interval on està la variable independent.

Estudiar una funció a trossos suposa estudiar cadascun dels intervals, però restringits al seu domini de definició.

Per calcular la imatge per un valor de la x s'utilitza una o altra expressió depenent de les condicions de cadascuna. Llavors el domini està format per tot el conjunt de valors de x els quals tenen imatge.

Veiem-ne alguns exemples.

Exemple 1

$f parèntesi esquerre x parèntesi dret igual obre claus taula fila cel·la taula atributs alineació columna left fin atributs fila cel·la x menys 1 espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai s i espai espai espai espai espai x menor o igual que menys 3 fi cel·la fila cel·la fracció numerador 1 entre denominador x més 2 fi fracció espai espai espai espai espai espai espai espai espai espai espai espai s i espai espai menys 3 menor que x menor que 0 fi cel·la fi taula fi cel·la fila cel·la x al quadrat més 2 espai espai espai espai espai espai espai espai espai espai espai espai espai s i espai espai 0 menor que x menor o igual que 1 fi cel·la fila cel·la 5 espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai s i espai espai espai espai espai espai espai espai x major o igual que 3 fi cel·la fi taula tanca$

té 4 trossos.

Intentem buscar imatges per alguns valors de x

f(-4)=(-4)-1=-5 (expressió 1a ja que -4≤-3)

f(-3)=(-3)-1=-4 (expressió 1a ja que -3≤-3)

f(-1)=1/(-1+2) =1 (expressió 2a ja que -3<-1<0)

f(-2)= 1/(-2+2)=1/0 que NO EXISTEIX (expressió 2a ja que -3<-2<0)

f(0)=NO EXISTEIX ja que no compleix cap de les 4 condicions

f(0'5)=(0'5)²+2=2'25 (expressió 3a ja que 0<0'5≤1)

f(1)=(1)²+2=3 (expressió 3a ja que 0<1≤1)

f(3)=5 (expressió 4a ja que 3≥3)

f(4'2)=5 (expressió 4a ja que 4'2≥3)

En definitiva estudiant cadascun dels trossos tenim:

- Si x≤ -3 llavors té imatge, la funció és polinòmica i es calcula substituint en l'expressió $x menys 1$
- Si $x pertany parèntesi esquerre menys 3 coma 0 parèntesi dret$ la funció és racional. Llavors té imatge, llevat del cas x= -2, valor on s'anul·la el denominador i es calcula substituint en l'expressió $fracció numerador 1 entre denominador x més 2 fi fracció$ .
- Si $x pertany parèntesi esquerre 0 coma 1 claudàtor dret$ llavors té imatge ( la funció és polinòmica) i es calcula substituint en l'expressió $x al quadrat més 2$
- Si x ≥ 3 llavors té imatge i val 5 (la funció és constant)

I per tant el $envoltori caixa D o m parèntesi esquerre f parèntesi esquerre x parèntesi dret parèntesi dret igual parèntesi esquerre menys infinit coma menys 2 parèntesi dret espai unió espai parèntesi esquerre menys 2 coma 0 parèntesi dret espai unió espai parèntesi esquerre 0 coma 1 claudàtor dret espai unió espai claudàtor esquerre 3 coma més infinit parèntesi dret fi envoltori$

Exemple 2:

Exemple 3

$f parèntesi esquerre x parèntesi dret igual obre claus taula atributs alineació columna left fin atributs fila cel·la fracció numerador x entre denominador x menys 3 fi fracció espai s i espai x menor que 0 fi cel·la fila cel·la x més 1 espai espai espai s i espai x major o igual que 2 fi cel·la fi taula espai tanca$

Aquesta funció té dos trossos diferenciats i fixa't que hi ha un conjunt de punts on no està definida: els valors entre 0 i 2. Perfer imatges de valors negatius ens haurem de mirar el tros de dalt i pels valors més grans o igual que 2 haurem de mirar la funció de baix i pels valors entre 0 i 2 no té expressió.

El primer tros és racional. En principi hem d'evitar dividir per 0. El denominador s'anul·la si x= 3, però en ser un valor positiu la seva imatge es faria aplicant la definició del segon tros, per tant el primer tros està ben definida per tots els negatius.

El segon tros és polinòmic i per tant no té cap problema de definició, està ben definida per tots els valors més grans o iguals a 0.

En definitiva l'únic problema de definició ve donat per com ens han definit la funció. Tenim doncs que $envoltori caixa D o m espai espai f espai igual espai normal nombres reals menys claudàtor esquerre 0 coma 2 parèntesi dret igual parèntesi esquerre menys infinit coma 0 parèntesi dret espai unió espai claudàtor esquerre 2 coma més infinit parèntesi dret fi envoltori$

Exercici

Observeu el gràfic següent, d'una funció polinòmica de tercer grau i indiqueu les qüestions següents:

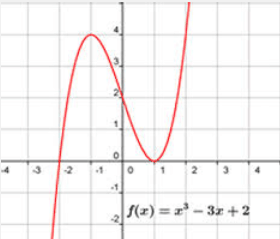
a) Calculeu la imatge de x = 1, i de x = 2

b) Calculeu les coordenades dels punts de tall de la funció amb l'eix X.

c) Calculeu les coordenades dels punts de tall de la funció amb l'eix Y.

d) Doneu les coordenades del màxim i del mínim relatius de la funció

e) Digueu en quins intervals la funció creix i en quins decreix.

Forma 1

En aquest problema coneixem la gràfica de la funció, per tant podem deduir totes les respostes simplement observant la gràfica

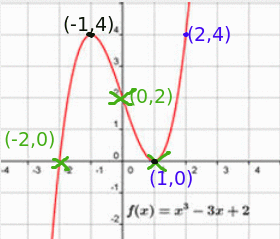
a) Observant la gràfica:

f(1) =0

f(2) =4

b) Punts de tall (-2,0) i (1,0). Són els punts en els que la gràfica toca l'eix X

c) Punts de tall (0,2) . És el punt en el que la gràfica toca l'eix Y

d) Màxim (-1,4) i Mínim (1,0)

e) La funció creix a l'interval $parèntesi esquerre menys infinit coma espai menys 1 parèntesi dret$ i a $parèntesi esquerre espai 1 coma espai més infinit parèntesi dret$ i decreix en els punts de l'interval $parèntesi esquerre menys 1 coma espai 1 parèntesi dret$ . (Observeu que els intervals es donen en funció de la x)

Forma 2

Si de la funció només es coneix la seva expressió algebraica ( y= x³-3x+2) i no la seva gràfica, podríem trobar algunes de les respostes.

a) f(1) = 1³- 3·(1) + 2 = 0

f(2) = 2³- 3·(2) + 2 = 4

b) Punts de tall amb l'eix X . Igualem a 0 la funció i en busquem les arrels. En tractar-se d'una equació de grau 3 cal aplicar el mecanisme de Ruffini.

$x al cub menys 3 x més 2 espai igual 0 F e n t espai R u f f i n i espai dos punts taula fila cel·la taula fila blank 1 0 cel·la menys 3 fi cel·la 2 fila 1 blank 1 1 cel·la menys 2 fi cel·la fila blank 1 1 cel·la menys 2 fi cel·la 0 fi taula fi cel·la fi taula taula fila blank 1 1 cel·la menys 2 fi cel·la fila 1 blank 1 2 fila blank 1 2 0 fi taula taula fila blank 1 2 fila cel·la menys 2 fi cel·la blank cel·la menys 2 fi cel·la fila blank 1 0 fi taula$

I s'obté com a solucions x=1 doble, i x=-2. Per tant els punts de tall són (1,0) i (-2,0)

d) Punts de tall amb l'eix Y, només caldria calcular la imatge de 0 per la funció f: f(0)

$f parèntesi esquerre 0 parèntesi dret igual 0 al cub menys 3 parèntesi esquerre 0 parèntesi dret més 2 espai igual 2 P u n t espai d e espai t a l l espai parèntesi esquerre 0 coma 2 parèntesi dret$

d) e) Els màxims i mínims i els intervals de creixement es poden trobar usant la derivada, concepte que treballaràs a segon.

Exercici

Una empresa de lloguer de cotxes ofereix dues modalitats de lloguer amb dos tipus de tarifes:
TARIFA A: 35€ per dia sense límit de km
TARIFA B: 10€ per dia i 0,20€ per km recorregut
Un turista vol llogar un cotxe per una setmana, a partir de quants km l'interessa una o l'altra modalitat?

Resolució

La solució es pot trobar de diferents formes, però una d'elles, seria fer una gràfica de cada una de les situacions, i en els mateixos eixos fet que ens permetrà fer comparacions.

El temps de lloguer és una setmana, per tant les variables a relacionar són x=km recorreguts i y=€ (preu)

Farem una taula de valors que després representarem en us eixos de coordenades.

Tarifa A			Tarifa B

x(km)	y(€)	x(km)	y(€)
200 km	35·7 =245€	200 km	10·7+0,2·200=110 €
500 km	35·7 =245€	500 km	10·7+0,2·500=170 €
1000 km	35·7 =245€	1000 km	10·7+0,2·1000=270 €
2000 km	35·7 =245€	2000 km	10·7+0,2·2000=470 €
3000km	35·7 =245€	3000 km	10·7+0,2·3000=670 €
x km	y=245	x km	y=70+0,2·x €

Els valors de "x" els hem triat a l'atzar. Però ens permeten observar que la resposta estarà entre 500 km i 1000km. Provant amb valors entre 500 i 1000 trobarien el nombre de Km a partir dels qual podem deduir quina tarifa és més interessant. A la darrera fila de la taula hem escrit l'expressió algebraica de les funcions

Per calcular exactament aquests km , sens e anar provant, cal resoldre els sistema format per les dues equacions algebraiques de les funcions:

la primera és constant, val sempre 245 independentment dels km recorreguts
la segona, és una funció lineal.

Per veure on es tallen les dues funcions resolem el sistema format per les dues expressions.

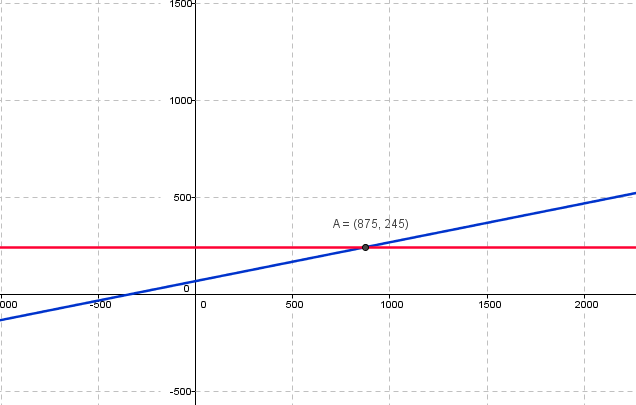
$obre claus taula atributs alineació columna left fin atributs fila cel·la y igual 245 fi cel·la fila cel·la y igual 70 espai més espai 0 coma 20 espai x fi cel·la fi taula tanca 245 espai igual espai 70 espai més espai 0 coma 20 espai x 245 menys 70 igual espai 0 coma 20 espai x 175 espai igual espai 0 coma 20 espai x fracció numerador 175 entre denominador 0 coma 20 fi fracció igual x x igual 875 espai k m$

La interpretació d'aquest càlcul és la següent:

Si el client fa més de 875 km, l'interessa la tarifa A (línia vermella de la gràfica)

SI el client fa exactament 875 km, les dues tarifes representarien el mateix cost.

Si el client fa menys de 875 km, l'interessa més la tarifa B (línia blava de la gràfica)

Gràfica:

Resum de funcions I

Descripció

Taula de continguts

El concepte de funció

Imatges i antiimatges

Exemples

Interpretació d'una gràfica

Exemple

Domini i recorregut

Domini

Què s'ha de tenir en compte en calcular el domini d'una funció?

Recorregut

Exemples

Exemples de càlcul de dominis

Exemples de càlcul de dominis

Punts de tall amb els eixos

Punts de tall amb l'eix d'abscisses (de les x)

Exemple

Punts de tall amb l'eix d'ordenades (de les y)

Exemple

Monotonia i extrems

Màxims i mínims

Funcions polinòmiques de grau 1. Rectes.

Exemple

Funcions quadràtiques. Paràboles.

Gràfica d'una paràbola

Exemple de paràbola 1

Exemple de paràbola 2

Talls amb l'eix x

Tall amb l'eix y

Vèrtex

Taula de valors

Gràfica

Exemple de paràbola 3

Talls amb l'eix x

Tall amb l'eix y

Vèrtex

Gràfica

Problema

Talls amb l'eix x

Tall amb l'eix y

Vèrtex

Altres tipus de funcions

Funcions racionals

Exemples

Funcions de proporcionalitat inversa. Hipèrboles

Treball en equip

Funcions definides a trossos

Exemple 1

Exemple 2:

Exemple 3

Exercici

Forma 1

Forma 2

Exercici

Resolució