Llibre resum dels continguts bàsics del lliurament 4.

Si tenim en compte únicament el cas de la correlació lineal (que és el nostre objectiu), se sol utilitzar l'anomenat coeficient de Pearson.

El coeficient de Pearson, r, d'una variable bidimensional (X,Y) és un paràmetre estadístic que es calcula a partir de l'expressió:

on

Procediment:

• Saber quina és la variable X, i quina és la variable Y
• Fem la taula de doble entrada
• A partir d'aquesta taula crearem 3 taules més:
  • La primera d'aquestes taules serà de la variable X. En les columnes hi situarem els valors      
  • La segona d'aquestes taules serà de la variable Y. En les columnes hi situarem els valors 
  • La tercera i última d'aquestes taules serà de la variable bidimensional XY. En les columnes hi situarem els valors 

Amb aquestes tres taules i la suma total de les seves columnes, podreu calcular tots els paràmetres:

• Mitjana, variància i desviació estàndard (o típica) de X
• Mitjana, variància i desviació estàndard (o típica) de Y
• Covariància
• Coeficient de correlació lineal de Pearson

Encara que són molts passos, sempre són els mateixos. I per tant si sabeu fer un problema d'aquest tipus, segur que sabreu fer-los tots.

Exemple :

S'ha realitzat una enquesta a 50 persones preguntant per el nombre de persones (X) que habiten la llar familiar i el nombre d'habitacions (Y) que té la casa. Els resultats obtinguts (x_i ,y_j) són els següents:

(3,4),(2,1),(2,4),(3,2),(3,2),(3,3),(2,1),(2,2),(2,2),(4,5),

(4,3),(2,2),(5,4),(4,3),(4,2),(4,3),(4,3),(3,2),(3,4),(4,4),

(5,4),(6,4),(3,2),(2,2),(2,2),(4,5),(4,3),(2,3),(3,3),(3,4),

(3,2),(5,3),(6,5),(6,4),(2,2),(5,4),(4,3),(4,2),(4,3),(4,3),

(1,1),(2,4),(3,2),(3,2),(1,2),(4,3),(4,4),(1,2),(4,5),(3,3)

La taula de doble entrada següent mostra la distribució de dades obtingudes

També podem considerar les variables X i Y com a variables unidimensionals si volem trobar els seus paràmetres estadístics com ara la mitjana i la desviació tipus. Aquestes variables es coneixen com a marginals. Observem que a partir de la informació bidimensional, sempre podem trobar les característiques de les variables marginals (X  i Y pensades separadament), només s'han de sumar files o columnes segons el cas. Un cop tenim les marginals, ja podem calcular-ne tots els paràmetres estadístics unidimensionals que ens calguin.

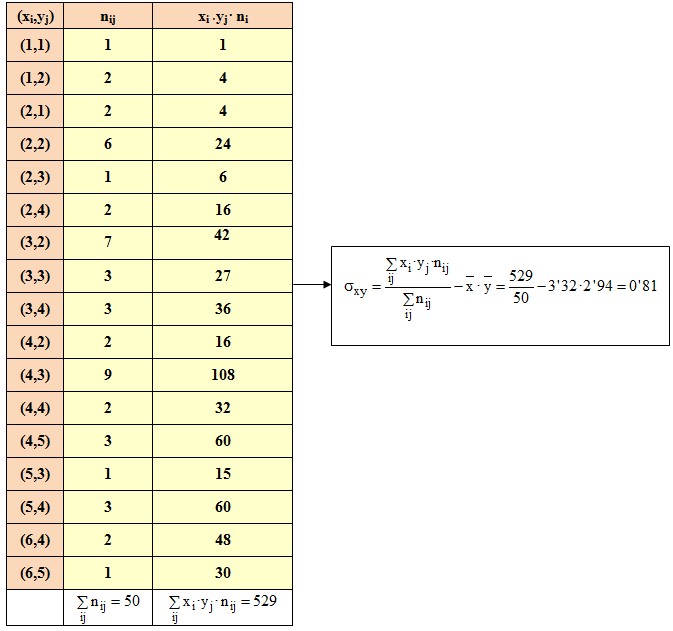
I ara finalment ja podem trobar el coeficient de Pearson:  

A partir d'aquest valor que podríem dir? Doncs que hi ha certa dependència lineal positiva entre les dues variable, en prendre el valor 0,61 veiem que la dependència és forta però tampoc massa.