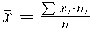Llibre resum dels continguts bàsics del lliurament 4.
| Sitio: | Cursos IOC - Batxillerat |
| Curso: | Matemàtiques I (Bloc 2) ~ gener 2020 |
| Libro: | Llibre resum dels continguts bàsics del lliurament 4. |
| Imprimido por: | Guest user |
| Día: | domingo, 19 de mayo de 2024, 11:33 |
Descripción
cc
Estadística descriptiva unidimensional
En aquest primer capítol del llibre, es recorden els principals conceptes de l'estadística unidimensional (és a dir, en la què s'estudia només una variable), per a poder posteriorment encarar l'estadística de dues variables o bidimensional. Si aquests conceptes ja els domines, pots passar directament al capítol 2.Què és l'estadística?
Avui dia difícilment podem llegir un diari o veure un telenotícies sense trobar-nos gràfics i estudis estadístics. És important conèixer els conceptes bàsics d'aquesta ciència per entendre i interpretar
críticament la informació que se'ns dóna.

L'estadística és una branca de les matemàtiques que té per objectiu recopilar, organitzar, analitzar i interpretar dades referides a un col·lectiu.
Primers conceptes
Convé conèixer el vocabulari específic que es fa servir en els estudis estadístics.Població: conjunt d'individus amb algunes característiques comunes sobre el què recau l'estudi. Mostra: subconjunt de la població sobre la què es fa l'estudi quan és impossible fer l'estudi exhaustiu sobre tota la població. La mostra cal que sigui representativa de tota la població, per tal que se'n puguin extraure resultats fiables.Quan més gran sigui la mostra, més fiable seran els resultats.
Variable estadística: és la propietat o característica de la població que estem interessats a estudiar. Es solen representar per lletres majúscules X, Y, Z...Hi ha molts tipus de variables i convé començar classificant-les segons diferents criteris.
Les dades són els valors concrets que pren aquesta variable estadística.
Exemple
Si fem un estudi sobre el nombre de germans que tenen els estudiants de Batxillerat a l'IOC, podríem passar una enquesta demanant quants germans té cada estudiant.
La població estaria formada per tots els estudiants de Batxillerat de l'IOC.
La variable en aquest cas seria el nombre de germans que té cada estudiant.
I les dades serien els resultats concrets: 0 germans, 1 germà, 2 germans, etc que respongués cada estudiant a la consulta.
Classificació de les dades
Si les classifiquem segons si les dades es poden o no comptar parlarem de variables estadístiques quantitatives i qualitatives.
- Les variables qualitatives prenen valors no numèrics, que no es poden mesurar. Dins d'aquest tipus encara podem separar les variables ordinals tals que tot i no ser numèriques podrien ser ordenades (per exemple molt, bastant, suficientment,
poc, gens) i les nominals que són atributs que no poden ser ordenats (colors, nacionalitats, etc)
- Les variables quantitatives prenen valors numèrics, les podem mesurar. Entre elles, distingim dos tipus: discretes i contínues.
- Les variables quantitatives discretes no poden prendre valors intermedis entre dos valors possibles consecutius.
- Les variables quantitatives contínues poden prendre valors intermedis entre dos valors tan propers com vulguem.
Exemples
- Sigui X la variable estadística que estudia el color del cotxe dels ciutadans d'una certa població. Aquesta variable pot prendre els valors
X={blanc, vermell, blau, verd, groc, negre,...} i és una variable qualitativa.
- Sigui Y
la variable estadística que estudia la llargada de les erugues de les
diferents espècies de papallones d'un determinat continent. Aquesta
variable pot prendre qualsevol nombre real que està dins l'interval
[0'5, 10] cm.
- Sigui Z la variable estadística que estudia el nombre de vegades que van al cinema mensualment els habitants d'una ciutat. Aquesta variable pot prendre els valors
Z={0, 1, 2, 3, 4, ....} i és una variable quantitativa discreta, observeu que entre 1 i 2 la variable no pot prendre els valors decimals intermedis, perquè no podem anar al cinema 1,3 vegades.
La classificació anterior la podem resumir en aquest quadre:
Es recomana consultar el document Conceptes bàsics d'estadística unidimensional (pag 1-2) on trobareu exemples i explicacions més detallades d'aquests primers conceptes.
Les taules
Tal com hem dit en un inici, en estudi estadístic comença recollint un conjunt molt gran de dades de diferents maneres: amb enquestes, amb l'observació directa, etc.
Un cop recollides les dades caldrà passar-les a net, és a dir organitzar-les, de manera que siguin de fàcil interpretació, per això es posen en una taula amb diverses columnes.
Aquestes taules les anomenem taules de freqüències. Aquí indiquem quins són els conceptes que habitualment es recullen a les taules i les seves notacions, tot i que cal tenir en compte que de vegades segons el llibre o l'estudi les notacions poden variar.
N= nombre total de dades recollides (o d'individus estudiats). És possible que algun llibre posi n en lloc de N, però segur que pel context ho veuràs.
| nom | notació | definició i càlcul |
| valor de la dada
|
xi | dada que ocupa el lloc i |
| freqüència absoluta | ni | indica el nombre de vegades que s'ha observat la dada xi |
| freqüència relativa | fi | |
| percentatge | fi% | |
| freq. absoluta acumulada | Ni | Ni=n1+n2+...+ni nombre de dades inferiors o iguals a xi |
| freq. relativa acumulada | Fi |
Com hem dit, aquestes notacions poden variar en funció del llibre, així en alguns llibres la notació és al revés: fi indica la freqüència absoluta i ni indica la freqüència relativa. Independentment de la notació que es faci
servir, fixa't que sempre: les freqüències absolutes prenen valors enters i la seva suma és el nombre total de dades i les freqüències relatives prenen valors decimals ( entre 0 i 1) i la seva suma dóna 1. Si estan donats en percentatge la suma dóna
100.
Les freqüències acumulades només tenen sentit per variables quantitatives, perquè el que ens indiquen és quantes dades hi ha inferiors o iguals a una donada.
Convé, si no coneixes massa aquests conceptes, que llegeixis amb atenció les pàgines 3-6 del document Conceptes bàsics d'estadística unidimensional que ja t'hem enllaçat abans. Hi trobaràs explicacions detallades i exemples senzills explicats.
Dades agrupades en intervals
En el cas de dades quantitatives continues o algunes discretes amb molts valors, es solen agrupar en intervals. En aquest cas interessa posar una columna amb l'interval [a,b) i una altra columna amb la marca de classe que notarem xi i que és
el punt mig de l'interval Veiem un exemple d'una taula on les dades estan recollides per intervals.

Fixa't que a la primera columna s'han separat 5 intervals. En aquest cas tots d'amplitud (distància entre els extrems de l'interval) 200.
A la segona columna s'han calculat les marques de classe, és a dir els punts mitjos dels intervals:
I a la darrera columna hi tenim les freqüències absolutes. Per exemple el primer 5 ens indica que de les dades estudiades n'hi ha 5 que estan entre 0 i 200, però no sabem quin valor exacte prenen: (podrien estar molt properes a 0, properes a 200, disperses
dins l'interval, centrades a prop de la marca de classe,...). Ara bé, quan passem a fer càlculs es treballarà com si les 5 dades fossin la marca de classe 100 i això naturalment fa perdre precisió, però aquesta pèrdua de precisió es compensa en la rapidesa
en què es podran fer els càlculs posteriors.
Els gràfics estadístics
Els gràfics estadístics ens permeten fer-nos una idea ràpida i visual sobre el comportament de la variable estudiada a partir d'un dibuix. N'hi ha de molts tipus. Els més importants són:
Diagrama de barres i polígon de freqüències
Aquests diagrames es fan amb variables qualitatives, o quantitatives discretes. Per fer-los cal:
- Dibuixar els eixos de coordenades.
- A l'eix d'abscisses es representa el valor de la variable i a l'eix d'ordenades la freqüència absoluta (o relativa).
- Per cada valor es dibuixa una barra que tingui com alçada la freqüència absoluta (o relativa)
- El polígon de freqüències es pot fer unint els punts mitjos dels extrems d'aquestes barres.
 |
 |
|---|
Histograma
És com el diagrama de barres però per variables agrupades en intervals.
- Cal dibuixar els eixos
- A l'eix d'abscisses es dibuixen els intervals i a l'eix d'ordenades les freqüències
- Per cada interval dibuixem un rectangle amb àrea proporcional a la freqüència. Si tots els intervals tenen la mateixa amplitud , tots els rectangles tenen la mateixa amplada i l'altura correspon a la freqüència

Diagrama de sectors
El podem fer per qualsevol tipus de variable
- Es dibuixa un cercle o semicercle i es divideix en tants sectors com valors pren la variable. L'amplitud de cada sector ha de ser proporcional a la freqüència absoluta o relativa.
- Per calcular l'amplitud de cada sector utilitzarem la següent fórmula.
(fixeu-vos que podeu fer-ho aplicant la regla de tres)
Paràmetres estadístics
Un cop tenim les dades endreçades en una taula, en el cas de les variables quantitatives interessa buscar-ne alguns paràmetres que ens aportin informació a partir d'un sol nombre.Hi ha paràmetres de molts tipus: de centralització, de dispersió, de simetria, de curtosis, etc, però ens centrarem bàsicament en els dos primers tipus.
Mesures de centralització
Ens indiquen on es situen els valors centrals de la distribució. Les principals són:
| NOM | COM ES CALCULA |
| Mitjana aritmètica |
És el valor que tindrien les dades si totes fossin iguals i sumessin el mateix. |
| Mediana Me |
Si la N és senar Me = dada que ocupa el lloc Si la N és parell Me = mitjana de les dades que ocupen el lloc És el valor que està just al mig de la distribució. La meitat de dades són iguals o superiors a la mediana i la meitat menors o iguals.
|
| Moda Mo | És la dada que té més freqüència, és a dir la que més és repeteix |
Convé molt que llegeixis amb deteniment els detalls i exemples que trobaràs en aquest document, sobretot fixa't molt bé en la interpretació de cada paràmetre: Mesures de centralització.
Mesures de dispersió
Fixa't en aquestes dues distribucions de dades:
A:1, 4, 4, 9.
B: 4, 4, 4, 4, 4, 5, 5, 6
En el cas A: la Mo=4, la Me=4 i la = 4,5.
En el cas B: la Mo=4, la Me=4 i la = 4,5.
Observa que coincideixen els tres paràmetres de centralització, en canvi a cop d'ull es veu que es tracta de dues distribucions prou diferents. Això ens fa pensar que ens calen altres paràmetres per fer un bon estudi.
Les mesures de dispersió ens donen una idea del grau de separació de les dades de la distribució.
Aquí tenim les fórmules principals. És especialment important que recordeu i sapigueu aplicar la fórmula de la variància i de la desviació típica. Observeu que es donen dues fórmules alternatives pel càlcul de la variància. Convé saber les dues i utilitzar
la que més convingui segons quines dades coneguem. A ser possible farem servir la segona opció, ja que això ens evitarà haver d'anar introduint parèntesis a la calculadora.
| NOM | COM ES CALCULA |
| Rang o recorregut R | |
| Desviació mitjana |
|
| Variància |
|
| Desviació típica |
El coeficient de variació
El coeficient de variació serveix per comparar dues distribucions diferents. Ens indica quina de les distribucions té menys dispersió i per tant una mitjana més representativa.
Quan més petit és el CV menys dispersió i més representativitat té la mitjana aritmètica de la distribució.
es calcula dividint la desviació típica entre la mitjana aritmètica.
Exercici resolt: estadística unidimensional
Les dades (en blau) de la taula inferior mostren els resultats d'uns esportistes en una prova de salt de perxa.
a) Completa la taula de freqüències omplint les caselles que falten.
|
mesura salt (metres) |
marca de classe |
Nombre d'esportistes (Freqüència absoluta) |
Freqüència absoluta acumulada |
Freqüència relativa arrodonir a dos decimals |
Freqüència relativa acumulada arrodonir a dos decimals |
xi*ni |
ni·xi 2
|
| [2, 2.5) | 6 | ||||||
| [2.5, 3) | 12 | ||||||
| [3, 3.5) | 15 | ||||||
| [3.5, 4) | 4 | ||||||
| TOTALS |
b) Calcula el rang.
c) Calcula la mitjana aritmètica.
d) Calcula quin % d'esportistes va saltar més 3.5 m.
e) Calcula la variància i la desviació típica.
a) Resposta
|
mesura salt (metres) |
marca de classe |
Nombre d'esportistes (Freqüència absoluta) |
Freqüència absoluta acumulada |
Freqüència relativa arrodonir a dos decimals |
Freqüència relativa acumulada arrodonir a dos decimals |
xi*ni |
ni·xi 2
|
| [2, 2.5) | 2.25 | 6 | 6 | 6/37=0.16 | 0.16 | 13.5 | 30,375
|
| [2.5, 3) | 2.75 | 12 | 18 | 12/37=0.32 | 0.48 | 33 | 90,75
|
| [3, 3.5) | 3.25 | 15 | 33 | 15/37=0.41 | 0.89 | 48.75 | 158,4375 |
| [3.5, 4) | 3.75 | 4 | 37 | 4/37=0.11 | 1 | 15 | 56,25 |
| TOTAL | 37 | 1 | 110.25 | 335,8125 |
b) El rang d'una variable estadística és la diferència entre el valor més gran i el valor més petit. Rang (X) =4-2=2
c) La mitjana aritmètica es calcula amb la fórmula:
d) Cal mirar la freqüència relativa de l'interval [3.5 , 4) i veiem que és 4/37=0,11→11%
És a dir , hi ha 4 esportistes dels 37 que hi ha en total que han saltat més de 3.5 m. O sigui l'11%
e) Disposem de dues fórmules pel càlcul de la variància, però a partir de la taula (darrera columna) ens convé fer servir
Substituïm els valors de la taula i els ja obtinguts a la fórmula:
m
Estadística bidimensional
Una variable estadística bidimensional
és la que resulta d'observar conjuntament dues característiques X i Y relatives a una mateixa població o mostra.
Cada observació d’un element de la mostra està representada per un parell de valors (x,y).
No
es tracta de fer un estudi aïllat de cadascuna de les variables, sinó
d’estudiar la relació o dependència que pugui existir entre elles, en el
cas que aquesta relació existeixi.
Exemple: La variable (X,Y) que recull les notes finals de matemàtiques i física respectivament dels alumnes d'una classe. Aquesta variable pot prendre els valors:
(X,Y)={(0,0),(0,1),(0,2),...(0,10),(1,0),(1,1),(1,2)....(1,10),(2,0),(2,1)...(2,10),........(10,0),(10,1),...(10,10)}
El conjunt de totes les dades procedents de l'observació d'una variable estadística bidimensional s'anomena distribució bidimensional.
Taules bidimensionals
La manera més habitual d’expressar els valors obtinguts en una distribució estadística bidimensional és mitjançant una taula de contingència o taula de doble entrada.
Al marge superior de la taula s’escriuen els resultats d’una de les variables i al marge esquerre, els valors de l’altra variable.
En les caselles de la taula s’indiquen simultàniament les freqüències absolutes, les freqüències relatives o els percentatges corresponents a les dues variables.
També s’acostuma a afegir al final de cada fila i de cada columna les anomenades distribucions marginals, que donen les distribucions unidimensionals de cadascuna de les variables per separat.
Les distribucions marginals de les variables X i Y s’obtenen a partir de la taula de contingència, considerant cada variable per separat. Representen les freqüències dels valors d’una variable, independentment dels valors de l’altra.
A partir de les distribucions marginals podem calcular la mitjana i la desviació típica de cadascuna de les variables, estudiant-les com una variable unidimensional.
Exemple
S'ha realitzat una enquesta a 50 persones preguntant pel nombre de persones (X) que habiten la llar familiar i el nombre d'habitacions (Y) que té la casa. Els resultats obtinguts (xi ,yj) són els següents:
(3,4),(2,1),(2,4),(3,2),(3,2),(3,3),(2,1),(2,2),(2,2),(4,5),
(4,3),(2,2),(5,4),(4,3),(4,2),(4,3),(4,3),(3,2),(3,4),(4,4),
(5,4),(6,4),(3,2),(2,2),(2,2),(4,5),(4,3),(2,3),(3,3),(3,4),
(3,2),(5,3),(6,5),(6,4),(2,2),(5,4),(4,3),(4,2),(4,3),(4,3),
(1,1),(2,4),(3,2),(3,2),(1,2),(4,3),(4,4),(1,2),(4,5),(3,3)
La taula de doble entrada següent mostra la distribució de dades obtingudes

La fila final en color blau correspon a la variable marginal de la X, observa que senzillament cal sumar totes les freqüències per columnes.
La columna final en color blau correspon a la variable marginal de la Y, observa que senzillament cal sumar totes les freqüències per files.
També podem considerar les variables X i Y com a variables unidimensionals si volem trobar els seus paràmetres estadístics com ara la mitjana i la desviació tipus

Exemple 2
En casos de poques dades o dades no repetides, és habitual que les taules es donin només en dues files (o dues columnes)
Per exemple una taula com aquesta
![]()
ens indica en cada columna l'observació d'un individu respecte a les dues variables observades.
Suposem que en aquest cas
X=nombre de vegades que va necessitar un individu per aprovar la teòrica del carnet de conduir.
i Y=nombre de vegades que va necessitar un individu per aprovar les pràctiques del carnet de conduir.
Doncs bé, aquesta taula treballa amb una mostra de 10 individus (les 10 columnes).
El primer individu va aprovar a la primera la teòrica i a la tercera les pràctiques, el segon va aprovar a la segona la teòrica i a la cinquena les pràctiques,....
En aquests casos de poques dades no és necessari fer la taula de contingència.
Què vol dir dependència estadística?
Entre dues variables diem que hi ha dependència estadística quan els valors que pren una variable estan relacionats d'alguna manera amb els valors que pren l'altra, possiblement no d'una manera exacte.
Aquesta dependència pot ser de molts tipus: quadràtica, exponencial, lineal, funcional, .... En general l'estudi del curs es basarà en la dependència lineal (és a dir, estudiar si el comportament d'una variable respecte a l'altra s'aproxima a una recta).
Quan les variables són de tipus quantitatiu, l'estudi de la dependència estadística es coneix com el problema de "regressió", i l'anàlisi del grau de dependència que hi ha entre les variables es coneix com el problema de correlació. L'objectiu principal de la regressió és descobrir la manera en què es relacionen.
Exemple
En una taula de pesos i altures de 10 persones es pot suposar que la variable "Alçada" influeix sobre la variable "Pes" en el sentit que pesos grans vénen explicats per valors grans d'altura (en general). De les dues variables a estudiar, que anomenarem amb X i Y, anomenarem a la X VARIABLE INDEPENDENT , i a l'altra (la Y) l'anomenarem VARIABLE DEPENDENT.
En la majoria dels casos la relació entre les variables és mútua, i és difícil saber quina variable influeix sobre l'altra. En l'exemple anterior, a una persona que pesa poc li suposarem menor altura i a una persona de poca altura li suposarem un pes més baix. És a dir, es pot admetre que cada variable influeix sobre l'altra de forma natural i per igual. Un exemple més clar on distingir entre variable independent i dependent és aquell on s'anota, de cada alumne d'una classe, el seu temps d'estudi (en hores) i la seva nota d'examen.
En aquest cas un petit temps d'estudi tendirà a obtenir una nota més baixa, i una nota bona ens indicarà que potser l'alumne ha estudiat molt. No obstant això, a l'hora de determinar quina variable depèn de l'altra, és clar que el "temps d'estudi" influeix sobre la "nota d'examen" i no al contrari, ja que l'alumne primer estudia un temps que pot decidir lliurement, i després obté una nota que ja no decideix arbitràriament. Per tant,
X = Temps d'estudi (variable independent)
Y = Nota d'examen (variable dependent)
Per detectar si hi ha algun tipus de relació de dependència entre dues variables és molt útil dibuixar-les per a visualitzar com és aquesta relació. Per això se sol utilitzar un gràfic anomenat núvol de punts o diagrama de dispersió consistent en representar sobre uns eixos de coordenades tots els parells de valors que apareguin en la mostra.
Habitualment es representa en l'eix d'abscises (X) la variable independent, i en l'eix de les ordenades (Y) la variable dependent.
En realitzar un diagrama de dispersió entre dues variables X i Y poden sorgir algunes de les següents situacions:
- Una relació matemàtica exacta entre X i Y, és a dir, donat un valor de X podem calcular el valor de la variable Y corresponent mitjançant una fórmula (dependència matemàtica).
- No s'observa cap relació entre les variables, és a dir, conèixer X no serveix en absolut per calcular Y (independència estadística).
- Tot i que no hi hagi una dependència matemàtica exacta, si que s'observa una relació aproximada (dependència estadística). Els punts s'acosten a la gràfica d'una funció
Exemples :

|

|
Hi ha una relació matemàtica exacte entre X i Y ja que |
|
|

|
No hi ha cap relació entre X i Y |
|
|
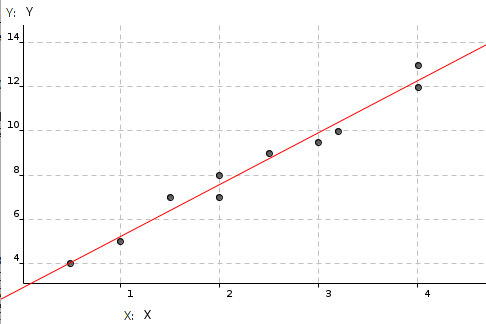
|
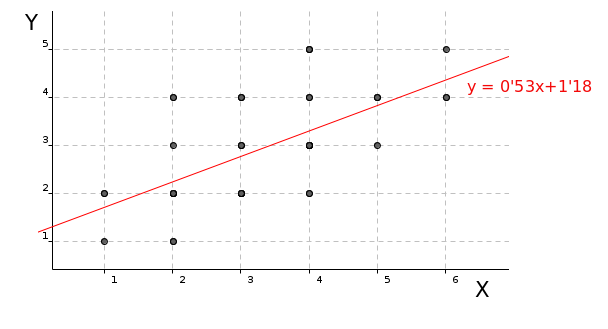
S'observa una relació aproximada o dependència estadística (i és lineal) |
|
|

|
S'observa una relació aproximada o dependència estadística (i no és lineal) |
El problema de trobar una relació funcional entre dues variables és molt complex, ja que hi ha infinitat de funcions de formes diferents. El cas més senzill de relació entre dues variables és la relació LINEAL, és a dir que Y = a + b X . És l'equació d'una recta on a i b són nombres, que és el cas en què ens centrarem en aquest curs
En concret el tercer núvol de punts es "semblant " a una recta. Si sabéssim calcular l'equació d'aquesta recta, es podria "aproximar" el valor de Y un cop conegut el valor de X. El problema de trobar l'equació de la recta que més s'assembli (o que millor s'ajusti) al núvol de punts es coneix com regressió lineal.
El primer núvol de punts és similar a l'últim, encara que en aquests cassos els núvols de punts s'aproximen a una corba i no a una recta. Trobar l'equació d'aquesta corba seria un problema de regressió no lineal.
Fórmules per variables bidimensioanals
Amb les variables bidimensionals, un cop s'han recollit les dades en taules interessa fer càlculs que ens ajudin a determinar el grau de dependència entre les dues variables.
La dependència entre dues variables pot ser lineal (recta) o funcional (altre tipus de funció). Per estudiar si dues variables tenen dependència lineal tenim diversos paràmetres.
Covariància
Tenim dues possibles fórmules per calcular la covariància entre dues variables X i Y. Triarem una o altra depenent del tipus de dades que disposem, tot i que en general és més ràpida la primera doncs no s'han d'introduir parèntesis a la calculadora.Es pot veure que la variància és com la covariància en cas que les dues variables fossin la mateixa.
Què ens indica el valor de la covariància entre dues variables? L'hem d'interpretar de la següent manera:
Si
Si
Si
Correlació
Coeficient de correlació
La correlació, que es calcula a partir de la covariància, a més de dir-nos si hi ha o no dependència de tipus lineal, ens dóna informació sobre el grau d'aquesta dependència. Ens diu si aquesta dependència és forta o fluixa.Si estudiem la correlació entre dues variables, podem mesurar-la quantitativament, mitjançant el coeficient de correlació lineal de Pearson r.
El coeficient de correlació és un nombre entre -1 i 1.
Com interpretarem la correlació r?
-
- -1≤ r ≤ 1 sempre
- Si r > 0 (nombre positiu), hi ha correlació lineal positiva o directa
- Si r < 0 (nombre negatiu), hi ha correlació lineal negativa o inversa
- Si r = -1 Les dues variables estaran correlacionades linealment de forma perfecta, i el núvol de punts es disposa exactament damunt d'una línia recta decreixent (a la pràctica rarament serà així)
- Si r = 1 Les dues variables estaran correlacionades linealment de forma perfecte, i el núvol de punts es disposa exactament damunt d'una d'una línia recta creixent (a la pràctica rarament serà així)
- Com més proper sigui r a -1, la correlació serà més forta i inversa
- Com més proper sigui r a 1, la correlació serà més forta i directa
- Com més proper sigui r a 0, la correlació serà més dèbil, és a dir el núvol de punts s'assemblarà menys a la recta.
Gràficament :
|
|
|
|
correlació positiva o directa, dèbil |
correlació positiva o directa, forta |
|
|

|
|
correlació negativa o inversa, forta |
No hi ha correlació |
Com es calcula el coeficient de correlació?
El coeficient de Pearson, r, d'una
variable bidimensional (X,Y) és un paràmetre estadístic que es calcula a
partir de l'expressió:
on
Procediment:
- Saber quina és la variable X, i quina és la variable Y
- Fem la taula de doble entrada
- A partir d'aquesta taula crearem 3 taules més:
- La primera d'aquestes taules serà de la variable X. En les columnes hi situarem els valors
- La segona d'aquestes taules serà de la variable Y. En les columnes hi situarem els valors
- La tercera i última d'aquestes taules serà de la variable bidimensional XY. En les columnes hi situarem els valors
- La primera d'aquestes taules serà de la variable X. En les columnes hi situarem els valors
Amb aquestes tres taules i la suma total de les seves columnes, podreu calcular tots els paràmetres:
- Mitjana, variància i desviació estàndard (o típica) de X
- Mitjana, variància i desviació estàndard (o típica) de Y
- Covariància
- Coeficient de correlació lineal de Pearson
Encara que són molts passos, sempre són els mateixos. I per tant si sabeu fer un problema d'aquest tipus, segur que sabreu fer-los tots.
Exemple :
S'ha realitzat una enquesta a 50 persones preguntant per el nombre de persones (X) que habiten la llar familiar i el nombre d'habitacions (Y) que té la casa. Els resultats obtinguts (xi ,yj) són els següents:
(3,4),(2,1),(2,4),(3,2),(3,2),(3,3),(2,1),(2,2),(2,2),(4,5),
(4,3),(2,2),(5,4),(4,3),(4,2),(4,3),(4,3),(3,2),(3,4),(4,4),
(5,4),(6,4),(3,2),(2,2),(2,2),(4,5),(4,3),(2,3),(3,3),(3,4),
(3,2),(5,3),(6,5),(6,4),(2,2),(5,4),(4,3),(4,2),(4,3),(4,3),
(1,1),(2,4),(3,2),(3,2),(1,2),(4,3),(4,4),(1,2),(4,5),(3,3)
La taula de doble entrada següent mostra la distribució de dades obtingudes

També podem considerar les variables X i Y com a variables unidimensionals si volem trobar els seus paràmetres estadístics com ara la mitjana i la desviació tipus. Aquestes variables es coneixen com a marginals. Observem que a partir de la informació
bidimensional, sempre podem trobar les característiques de les variables marginals (X i Y pensades separadament), només s'han de sumar files o columnes segons el cas. Un cop tenim les marginals, ja podem calcular-ne tots els paràmetres estadístics
unidimensionals que ens calguin.


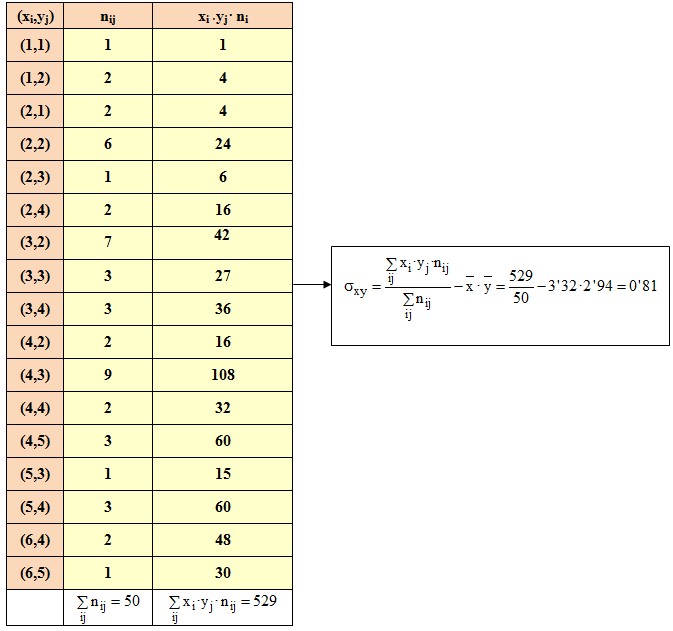
I ara finalment ja podem trobar el coeficient de Pearson:
A partir d'aquest valor que podríem dir? Doncs que hi ha certa dependència lineal positiva entre les dues variable, en prendre el valor 0,61 veiem que la dependència és forta però tampoc massa.
Recta de regressió
En una distribució bidimensional, una vegada constatada la correlació lineal entre les dues variables, mitjançant el coeficient de correlació lineal de Pearson (r) es poden fer estimacions, és a dir prediccions de valors possibles d'una variable.
Per fer aquestes prediccions, s'ha de calcular una recta de regressió, és a dir s'ha de buscar l'expressió algebraica de la recta que aproxima millor el núvol de punts.
Hi ha dues rectes de regressió que es calcularan en funció de la correlació i les mitjanes i variàncies de les variables marginals:
| La de Y sobre X | |
| La de X sobre Y |
La utilització d'una o l'altra depèn del context del problema. En ocasions l'enunciat ja diu quina recta utilitzar. En altres ocasions cal deduir-ho en funció de les dades.
Si es demana predir un valor de y donat el valor de x, cal usar la recta de Y sobre X, ja que és la recta en la que queda aïllada la Y.
Si es demana predir el valor de x coneixent la y corresponent, cal usar la recta de regressió de X sobre Y, ja que és la recta en la que queda aïllada la X.
La recta de regressió correspon a la recta que millor s'ajusta a la distribució de punts (núvol de punts).
Per exemple en la distribució bidimensional d'aquest notes:
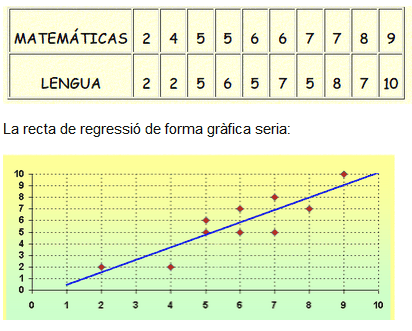
Procediment pel càlcul de la recta
- Saber quina és la variable X, i quina és la variable Y
- Fer una taula amb les columnes: valors de X, valors de Y , valors de X², valors de Y², valors de XY i els totals.
Amb aquestes columnes i la suma total d'aquestes columnes, es podran calcular tots els paràmetres:
- Mitjana, variància i desviació estàndard (o típica) de X
- Mitjana, variància i desviació estàndard (o típica) de Y
- Covariància
- Coeficient de correlació lineal de Pearson
- Recta de regressió de Y sobre X o bé Recta de regressió de X sobre Y
- Fer una predicció
Encara que són molts passos, sempre són els mateixos. I per tant si sabeu fer un problema d'aquest tipus, segur que sabreu fer-los tots.
Exemple
En la taula següent es donen les notes del test de aptitud (X) de sis aspirants a venedors i Y vendes realitzades per cada un, durant el primer mes, en cents d'euros.

a) Calcular "r" i interpretar el resultat
b) Trobar la recta de regressió de Y sobre X. Predir les vendes d'un venedor que tingui 47 en el test.
Resolució:



Observem que "r" és molt proper a 1, per tant la correlació lineal és forta i directa. A més nota en el test, més vendes és possible que faci l'aspirant.
r ens indica que les dues variables estan fortament relaciones, i per tant la predicció que ha sortit aplicant la recta de regressió, és fiable.
Després dels càlculs hem arribat a la conclusió que un aspirant amb 47 punts en el test, és probable que vengui per un valor de 76,41 cents d'euros = 7641 €
Exemple de regressió II
Seguint amb l'exemple treballat en el punt 2.4 on s'estudiaven les variables X= nombre d'habitants en una llar, Y=nombre d'habitacions.
En el punt 2.4 estaven fets els càlculs fins a trobar el coeficient de correlació de Pearson. Ara anem ara a cercar-ne la recta de regressió de Y sobre X.
Si volem ara per exemple inferir quantes habitacions tindrà una llar on hi visquin 4 persones sols hem de substituir la x per 4
Si fem el núvol de punts o diagrama de dispersió consistent de tots els parells de valors que apareguin en la mostra i també hi dibuixem la recta de regressió tindrem: