Print bookPrint book

Equacions i funcions exponencials i logarítmiques

Site: Cursos IOC - Batxillerat
Course: Matemàtiques aplicades a les C. socials I (Bloc 1) ~ gener 2020
Book: Equacions i funcions exponencials i logarítmiques
Printed by: Gast
Date: Sunday, 19 May 2024, 7:35 AM

Description

Equacions i funcions exponencials i logarítmiques

Table of contents

Potències i les seves propietats

La potència d'un nombre ens indica que el nombre està multiplicat per si mateix les vegades que indica l'exponent.

a to the power of x equals stack stack a times a times... times a space with overbrace on top with x on top   a space é s space l a space b a s e space d e space l a space p o t è n c i a space i space x space l apostrophe e x p o n e n t
5 cubed equals 5 times 5 times 5 equals 125

a to the power of 0 equals 1 a to the power of 1 equals a a to the power of m times a to the power of n equals a to the power of m plus n end exponent a to the power of m over a to the power of n equals a to the power of m minus n end exponent left parenthesis a to the power of m right parenthesis to the power of n space equals space a to the power of m times n end exponent left parenthesis a times b right parenthesis to the power of m equals a to the power of m times a to the power of n

open parentheses a over b close parentheses to the power of n equals a to the power of n over b to the power of n


         Potències                 Exemples

          a to the power of 0 equals 1 space space space space space space space space space space space space space space space space rightwards arrow space space space space 5 to the power of 0 equals 1 a to the power of s times a to the power of t equals a to the power of s plus t end exponent space space space space rightwards arrow space space space space 3 squared times 3 to the power of 5 equals 3 to the power of 2 plus 5 end exponent space equals 3 to the power of 7 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space 10 cubed times 10 to the power of negative 5 end exponent equals 10 to the power of 3 minus 5 end exponent equals 10 to the power of negative 2 end exponent space space space space space space space space space space space space a to the power of s over a to the power of t equals a to the power of s minus t end exponent space space space space space space space rightwards arrow space space space 7 squared over 7 to the power of 5 equals 7 to the power of 2 minus 5 end exponent equals 7 to the power of negative 3 end exponent equals 1 over 7 cubed space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space 10 cubed over 10 to the power of 7 equals 10 to the power of negative 4 end exponent space open parentheses a to the power of s close parentheses to the power of n equals a to the power of s times n end exponent space space space space rightwards arrow space space space space left parenthesis 2 cubed right parenthesis to the power of 5 equals 2 to the power of 15 space space space space space space space space space space space space space space space space space space space space space space space space space space space a to the power of negative n end exponent equals 1 over a to the power of n space space space space space space space rightwards arrow space space space space space 3 to the power of negative 5 end exponent equals 1 over 3 to the power of 5 space space space space space a to the power of 1 divided by n end exponent equals n-th root of a space space space space space space space rightwards arrow space space space space space 5 to the power of 1 divided by 3 end exponent equals cube root of 5 space space space space space space a to the power of s divided by n end exponent equals n-th root of a to the power of s end root space space space space space rightwards arrow space space space space space 5 to the power of 2 divided by 3 end exponent equals cube root of 5 squared end root space space space space

   


El nombre e

El nombre e és un nombre irracional.

Recordem que els nombres irracionals tenen infinites xifres decimals no periòdiques. És per això que els expressem amb un símbol, com per exemple el nombre Π

les primeres xifres (les podeu obtenir amb la calculadora) del nombre e són:

                      e = 2,71828....

Aquest nombre surt com a límit d'una successió, però no entrarem en el seu estudi en aquest bloc.

A un logaritme en base el nombre e el diem logaritme neperià i el representem com ln


Funcions exponencials

Si a l'expressió d'una funció apareix la variable independent x en un exponent, diem que tenim una funció exponencial.

f left parenthesis x right parenthesis equals k a to the power of x   a m b space a space u n space n o m b r e space r e a l space p o s i t i u space i space d i f e r e n t space d e space 1

Característiques de les funcions exponencials

Les característiques d'aquestes funcions són:

  • El domini són tots els R
  • El recorregut són tots els R positius
  • Totes tallen a l'eix de les y en el punt (0,1) perquè a⁰=1 per tota a
  • Si a>1 el gràfic és creixent i quan x pren valors molt petits (cap a -∞) el gràfic s'acosta a l'eix horitzontal, és a dir a la recta y=0. (asímptota)
  • Si 0<a<1 el gràfic és decreixent i quan x es fa molt gran (cap a +∞) el gràfic s'acosta a l'eix horitzontal, , és a dir a la recta y=0. (asímptota)




Com varia el gràfic d'una funció exponencial en variar-ne la base?

La relació és total: si la base "a" de la funció exponencial f left parenthesis x right parenthesis equals a to the power of x és un nombre major que 1 o està entre 0 i 1 el gràfic és molt diferent.

  • Si la base a > 1:
    Observeu a la imatge que tots els gràfics són funcions creixents. A més per valors positius, quan més gran és la base, més gran és la imatge.
    Com 3 greater than 2.5 greater than 2 greater than 1.5 rightwards arrow 3 to the power of x greater than open parentheses 2.5 close parentheses to the power of x greater than 2 to the power of x greater than open parentheses 1.5 close parentheses to the power of x space space p e r space t o t space x greater than 0.
    Pels negatius passa el contrari, és a dir 3 to the power of x less than open parentheses 2.5 close parentheses to the power of x less than 2 to the power of x less than open parentheses 1.5 close parentheses to the power of x space space p e r space t o t space x less than 0 
  • Si la base 0 < a < 1 :
Observeu a la imatge que tots els gràfics són funcions decreixents. A més per valors negatius, quan més gran és la base, més petita és la imatge.
Com 0.7 greater than 0.6 greater than 0.5 greater than 0.4 rightwards arrow open parentheses 0.7 close parentheses to the power of x less than open parentheses 0.6 close parentheses to the power of x less than open parentheses 0.5 close parentheses to the power of x less than open parentheses 0.4 close parentheses to the power of x space space p e r space t o t space x less than 0.
Pels positius passa el contrari, és a dir open parentheses 0.7 close parentheses to the power of x greater than open parentheses 0.6 close parentheses to the power of x greater than open parentheses 0.5 close parentheses to the power of x greater than open parentheses 0.4 close parentheses to the power of x space space p e r space t o t space x greater than 0


Què és una equació exponencial?

Una equació exponencial és aquella en què la incògnita apareix a l'exponent d'una potència.
És important a l'hora de resoldre equacions d'aquest tipus recordar les propietats bàsiques de les potències.

Tipus d'equacions exponencials

Hi ha molts tipus d'equacions exponencials, però majoritàriament (dins el temari de 1r de batxillerat) ens trobarem amb aquests dos tipus d'equacions :

  1. Equacions on totes les bases de les potències que surten (on la incògnita està en l'exponent) són reduïbles a una mateixa base
    • Sols hi ha un terme a cada membre de la igualtat.
      Exemples :
      • rightwards arrow space space 5 to the power of x squared plus 1 end exponent equals 125 space space space space space space space space space space left parenthesis 125 space equals 5 cubed right parenthesis rightwards arrow space space 2 to the power of 1 minus x squared end exponent equals 1 over 8 space space space space space space space space space space space space left parenthesis 1 over 8 space equals 2 to the power of negative 3 end exponent right parenthesis rightwards arrow open parentheses 10 to the power of X minus 1 end exponent close parentheses to the power of space X end exponent equals 100 space space space space space left parenthesis 100 space equals 10 squared right parenthesis
    • Com a mínim en un membre hi ha diverses potències que se sumen i totes tenen la mateixa base. Per resoldre aquestes les reduirem al cas anterior o a una equació de segon grau
      Exemples :
      rightwards arrow space space 3 to the power of x plus 3 to the power of x plus 1 end exponent plus 3 to the power of x plus 2 end exponent equals 9477 space space space left parenthesis t o t e s space l e s space p o t è n c i e s space t e n e n space b a s e space 3 right parenthesis rightwards arrow space 2 to the power of 2 x end exponent minus 20 times 2 to the power of x minus 384 equals 0 space space space space space space space space space left parenthesis t o t e s space l e s space p o t è n c i e s space t e n e n space b a s e space 2 right parenthesis

    • Com a mínim en un membre hi ha diverses potències que es sumen i totes les bases són potències del mateix nombre. Per resoldre aquestes les reduirem a una equació de segon grau.
      Exemples :

      rightwards arrow space space 4 to the power of x plus 1 end exponent plus 2 to the power of x plus 3 end exponent equals 320 space space space space space space space space left parenthesis t o t e s space l e s space p o t è n c i e s space t e n e n space b a s e space u n a space p o t è n c i a space d e space 2 right parenthesis rightwards arrow space space 9 to the power of x minus 6 times 3 to the power of x plus 1 end exponent plus 81 equals 0 space space space space left parenthesis t o t e s space l e s space p o t è n c i e s space t e n e n space b a s e space u n a space p o t è n c i a space d e space 3 right parenthesis

  2. Equacions on les bases de les potències que surten NO són reduïbles a una única base. Per resoldre aquestes cal utilitzar els logaritmes.
Exemples:

rightwards arrow space space 4 to the power of x plus 1 end exponent equals 3 rightwards arrow space space 9 to the power of x equals 2 to the power of x plus 1 end exponent


Resolució d'equacions exponencials 1

Veiem com es resolen els tipus d'equacions exponencials que treballarem en aquest curs.


Exemples 

bold 2 to the power of bold x bold equals bold 32

             2 to the power of x equals 2 to the power of 5 space space space space rightwards double arrow space bold italic x bold equals bold 5

bold 9 to the power of bold x bold equals bold 1 over bold 27 open parentheses 3 squared close parentheses to the power of bold x equals 1 over 3 cubed 3 to the power of 2 x end exponent equals 3 to the power of negative 3 end exponent space space space space rightwards double arrow space space 2 x equals negative 3 space space rightwards double arrow space space bold space bold italic x bold equals bold minus bold 3 over bold 2  

bold 8 to the power of bold minus bold x bold plus bold 10 end exponent bold equals bold 64 D e s c o m p o s e m space space e l space 64 space i space e l space 8 space 64 table row cell table row 64 2 row 32 2 row 16 2 row 8 2 row 4 2 row 2 2 row 1 blank end table end cell end table 64 equals 2 to the power of 6 i space j a space s a b e m space q u e space 2 cubed comma space l l a v o r s colon space q u e d a space d o n c s space colon space space space space space space space space space space space space space left parenthesis 2 cubed right parenthesis to the power of negative x plus 10 end exponent equals 2 to the power of 6 space space space space space space space space space space space space space space 2 to the power of 3 times left parenthesis negative x plus 10 right parenthesis end exponent equals 2 to the power of 6 I g u a l e m space e l s space e x p o n e n t s space j a space q u e space l e s space d u e s space p o t è n c i e s space t e n e n space l a space m a t e i x a space b a s e space space space space space space space space space space space space space space 3 times left parenthesis negative x plus 10 right parenthesis equals 6 space space space space space space space space space space space space space space space space space space minus 3 x plus 30 equals 6 space space space space space space space space space space space space space space space space space space space space minus 3 x equals negative 24 space space space space rightwards arrow space space x equals fraction numerator negative 24 over denominator negative 3 end fraction equals bold 8 space space space space space space space space space space space space space

bold 3 to the power of bold x bold equals fraction numerator bold 1 over denominator square root of bold 27 end fraction

3 to the power of x equals 1 over open parentheses 3 cubed close parentheses to the power of 1 divided by 2 end exponent 3 to the power of x equals 1 over 3 to the power of begin display style bevelled 3 over 2 end style end exponent equals 3 to the power of negative 3 divided by 2 space end exponent space space space space rightwards double arrow space space bold italic x bold equals bold minus bold 3 over bold 2


bold 2 bold times bold 25 to the power of bold x bold equals bold 10 bold times bold 5 to the power of bold x bold minus bold 2 end exponent up diagonal strike 2 times open parentheses 5 squared close parentheses to the power of x equals up diagonal strike 2 times 5 times 5 to the power of x minus 2 end exponent space space space space space space space space 5 to the power of 2 x end exponent equals 5 to the power of 1 plus x minus 2 end exponent space space space space space space space space space 5 to the power of 2 x end exponent equals 5 to the power of x minus 1 space space end exponent rightwards double arrow space space 2 x equals x minus 1 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space 2 x minus x equals negative 1 space rightwards arrow space space space space bold italic x bold equals bold minus bold 1

Observació important:

fixeu-vos que en aquest exemple i en tots els exemples anteriors sempre podem expressar els termes com a potencies d'un mateix nombre. O sigui, sempre arribem a una igualtat de potencies de la mateixa base.  En l'exemple anterior:

       space space space space space space space space space 5 to the power of 2 x end exponent equals 5 to the power of x minus 1 space space end exponent

i el raonament que fem és "igualtat de potencies de la mateixa base, implica igualtat d'exponents": 

                 space space space space space space space space space 5 to the power of 2 x end exponent equals 5 to the power of x minus 1 space space end exponent rightwards double arrow 2 x equals x minus 1

Què fem si no podem expressar els termes en la mateixa base?

Per exemple:   2 to the power of x equals 5 

En aquest cas hem d'aplicar logaritmes. Però això ho veurem en els apartats posteriors quan estudiem logaritmes.  


Resolució d'equacions exponencials 2

  1. Equacions on totes les bases de les potències que surten (on la incògnita està en l'exponent) són reduïbles a una mateixa base
    • Sols hi ha un terme a cada membre de la igualtat.
      Exemples :
      • rightwards arrow space space 5 to the power of x squared plus 1 end exponent equals 125 space space space space space space space space space space left parenthesis 125 space equals 5 cubed right parenthesis space space space space space space space R e s o l u c i ó colon space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space 5 to the power of x squared plus 1 end exponent equals 5 cubed space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space x squared plus 1 equals 3 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space x squared equals 2 space space space space rightwards arrow box enclose space space x space equals plus-or-minus square root of 2 space space space end enclose space space space space space space space space space space space space space space space space space space space space space space space space space space space space rightwards arrow space space 2 to the power of 1 minus x squared end exponent equals 1 over 8 space space space space space space space space space space space space space left parenthesis 1 over 8 space equals 2 to the power of negative 3 end exponent right parenthesis space space space space space space space R e s o l u c i ó colon space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space 2 to the power of 1 minus x squared end exponent equals 2 to the power of negative 3 end exponent space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space 1 minus x squared equals negative 3 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space x squared equals 4 space space space space rightwards arrow box enclose space space x space equals plus-or-minus 2 space space space end enclose space space space space space space space space space space space space rightwards arrow open parentheses 10 to the power of X minus 1 end exponent close parentheses to the power of space X end exponent equals 100 space space space space space space space left parenthesis 100 space equals 10 squared right parenthesis space space space space space space space R e s o l u c i ó colon space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space 10 to the power of x squared minus x end exponent equals 10 squared space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space x squared minus x equals 2 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space x squared minus x minus 2 equals 0 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space x equals fraction numerator 1 plus-or-minus square root of 1 plus 8 end root over denominator 2 end fraction equals fraction numerator 1 plus-or-minus 3 over denominator 2 end fraction rightwards arrow space space box enclose table row cell x subscript 1 equals space 2 end cell row cell space space x subscript 2 equals space minus 1 end cell end table end enclose
        Observem que en tots els casos hem arribat a dues potències amb la mateixa base. Dues potències de la mateixa base són iguals, si són iguals els exponent i això és el que fem per acabar les equacions.


    • Com a mínim en un membre hi ha diverses potències que es sumen i totes tenen la mateixa base. Per resoldre aquestes les reduirem al cas anterior o a una equació de segon grau. La resolució passa per escriure totes les potències amb la mateixa base
      Exemples :

    • bold 2 to the power of bold x bold plus bold 3 end exponent bold minus bold 3 bold times bold 2 to the power of bold x bold equals bold 40

      Aquest és un exercici tipus. 

    • Un error greu seria sumar els exponents (fixeu-vos que la propietat és "producte de potencies de la mateixa base es sumen exponents  am·an=am+n  però no hi ha cap propietat de la suma de potències (encara que tinguin el mateix exponent!). 

      Per fer aquests tipus d'exercici tindrem en compte les propietats:

                        box enclose a to the power of n plus m end exponent equals a to the power of n times a to the power of m a to the power of n minus m end exponent equals a to the power of n over a to the power of m end enclose

      Per tant tenim, 

           2 to the power of x times 2 cubed minus 3 times 2 to the power of x equals 40

          Per simplificar fem el canvi:  t equals 2 to the power of x

           t times 8 minus 3 times t equals 40 8 t minus 3 t equals 40 space space space rightwards arrow 5 t equals 40 space space rightwards arrow t equals 40 over 5 equals 8

          t equals 8 2 to the power of x equals 2 cubed space space space rightwards arrow space bold italic x bold equals bold 3    

      bold 5 to the power of bold x bold plus bold 1 end exponent bold plus bold 5 to the power of bold x bold minus bold 2 end exponent bold plus bold 5 to the power of bold x bold equals bold 151 over bold 25

      Aquest exercici és del mateix tipus que l'anterior.    

      Tenim:   

         5 to the power of x plus 1 end exponent equals 5 to the power of x times 5 to the power of 1 

         5 to the power of x minus 2 end exponent equals 5 to the power of x times 5 to the power of negative 2 end exponent equals 5 to the power of x over 5 squared

        Així doncs l'equació queda:

         5 to the power of x plus 1 end exponent plus 5 to the power of x minus 2 end exponent plus 5 to the power of x equals 151 over 25
          5 to the power of x times 5 to the power of 1 plus 5 to the power of x over 5 squared plus 5 to the power of x equals 151 over 25
        Fem el canvi:   t equals 5 to the power of x


          5 t plus t over 25 plus t equals 151 over 25 fraction numerator 5 times 25 t plus t plus 25 t over denominator up diagonal strike 25 end fraction equals fraction numerator 151 over denominator up diagonal strike 25 end fraction left parenthesis 125 plus 1 plus 25 right parenthesis t equals 151 space space rightwards arrow 151 t equals 151 space rightwards arrow space space t equals 1 

          Per tant,  space 5 to the power of x space equals 1 space space space space space rightwards double arrow space bold space bold italic x bold equals bold 0


      bold 9 to the power of bold x bold minus bold 4 bold times bold 3 to the power of bold x bold plus bold 3 bold equals bold 0

      Aquest és un altre exercici tipus.

      Veiem que tenim un terme amb 3 to the power of x i altre terme open parentheses 3 squared close parentheses to the power of x o el que és el mateix, open parentheses 3 to the power of x close parentheses squared , per tant l'equació és: 

          open parentheses space 3 to the power of x close parentheses squared space minus 4 times 3 to the power of x plus 3 equals 0

         Fem el canvi:    t equals 3 to the power of x   

          t squared minus 4 t plus 3 equals 0

          t equals fraction numerator 4 plus-or-minus square root of 4 squared minus 4 times 1 times 3 end root over denominator 2 times 1 end fraction equals fraction numerator 4 plus-or-minus square root of 16 minus 12 end root over denominator 2 end fraction equals fraction numerator 4 plus-or-minus square root of 4 over denominator 2 end fraction equals fraction numerator 4 plus-or-minus 2 over denominator 2 end fraction equals table row cell up right diagonal ellipsis fraction numerator 4 plus 2 over denominator 2 end fraction equals 6 over 2 equals 3 end cell row cell down right diagonal ellipsis fraction numerator 4 minus 2 over denominator 2 end fraction equals 2 over 2 equals 1 end cell end table

         Hem trobat dos valors per a t i recordem que   t equals 3 to the power of x  

         Obtenim les dues solucions:  

           3 to the power of x equals 3 space space rightwards double arrow space bold italic x bold equals bold 1 

           i

           3 to the power of x equals 1 space space space rightwards double arrow bold space bold italic x bold equals bold 0   


      rightwards arrow space space 3 to the power of x plus 3 to the power of x plus 1 end exponent plus 3 to the power of x plus 2 end exponent equals 9477 space space space left parenthesis t o t e s space l e s space p o t è n c i e s space t e n e n space b a s e space 3 right parenthesis space space space space space space R e s o l u c i ó colon space space space space space space space space space space space space space space space space space space space space space space space space space space space space 3 to the power of x plus 3 times 3 to the power of x plus 3 squared times 3 to the power of x equals 9477 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space left parenthesis 1 plus 3 plus 9 right parenthesis times 3 to the power of x equals 9477 space space space space space space space space space space space space space space space space space space space space space space space space space space space space 13 times 3 to the power of x equals 9477 space space space space space space space space space space space space space space space space space space space space space space space space space space space space 13 times 3 to the power of x equals 13 times 3 to the power of 6 rightwards arrow 3 to the power of x equals fraction numerator up diagonal strike 13 times 3 to the power of 6 over denominator up diagonal strike 13 end fraction rightwards arrow space box enclose space x equals 6 space end enclose rightwards arrow space 2 to the power of 2 x end exponent minus 20 times 2 to the power of x minus 384 equals 0 space space space space space space space space space left parenthesis t o t e s space l e s space p o t è n c i e s space t e n e n space b a s e space 2 right parenthesis space space space space space R e s o l u c i ó colon space space space space space space space space space space space space space space space space space space space space space space space space space space space open parentheses space 2 to the power of x close parentheses squared minus 20 times 2 to the power of x minus 384 equals 0 space space space space space space space space space space space space space space space space space space space space space space space space space space space F e m space e l space c a n v i space d e space v a r i a b l e space space 2 to the power of x equals t space space space space space space space space space space space space space space space space space space space space space space space space space space space space t squared minus 20 t minus 384 equals 0 space space space space space space space space space space space space space space space space space space space space space space space space space space space space t equals fraction numerator 20 plus-or-minus square root of 400 plus 1536 end root over denominator 2 end fraction equals fraction numerator 20 plus-or-minus 44 over denominator 2 end fraction rightwards arrow table row cell t subscript 1 equals 32 space end cell row cell t subscript 2 equals negative 12 end cell end table space space space space space space space space space space space space space space space space space space space space space space space space space space A r a space d e s f e m space e l space c a n v i space d e space v a r i a b l e colon space space space space space space space space space space space space space space space space space space space space space space space space space space P e r space t equals 32 rightwards arrow 2 to the power of x equals 32 rightwards arrow 2 to the power of x equals 2 to the power of 5 space space rightwards arrow space box enclose space x equals 5 space end enclose space space space space space space space space space space space space space space space space space space space space space space space space space space P e r space t equals negative 12 rightwards arrow 2 to the power of x equals negative 12 rightwards arrow N O space h i space h a space s o l u c i ó space j a space q u e space 2 to the power of x greater than 0

    • Com a mínim en un membre hi ha diverses potències que es sumen i totes les bases són potències del mateix nombre. Per resoldre aquestes les reduirem a una equació de segon grau.

  2. Equacions on les bases de les potències que surten NO són reduïbles a una única base. Per resoldre aquestes cal utilitzar els logaritmes.
    Per tant les reservem per més endavant.

En aquest document tens altres exemples d'equacions exponencials resoltes, consulta'l.

Què és un logaritme i per a què els utilitzem?

El logaritme és una operació matemàtica íntimament lligada amb les potències.

La seva definició és la següent:

box enclose bold l bold o bold g subscript bold a bold b bold equals bold x bold left right double arrow bold a to the power of bold x bold equals bold b bold comma bold space bold a bold greater than bold 0 end enclose Com la a és positiva la b també sempre ho serà.

A la a l'anomenem base del logaritme i només té sentit si aquesta és positiva.

En paraules podríem dir que el logaritme de b en base a, és el nombre al qual hem d'elevar la a per tal que ens doni b.

Les propietats dels logaritmes, que es deriven de les propietats de les potències, transformen els productes en sumes (recordar que a to the power of x times a to the power of y equals a to the power of x plus y end exponent) i aquest és el fet principal que va portar als matemàtics del segle XVI-XVII a "idear" els logaritmes. En aquella època el comerç i els avenços en l'àmbit de l'astronomia requerien fer càlculs amb nombres molt grans, però tenien el problema que no existien els avenços tecnològics que avui dia ens permeten fer càlcul amb moltíssimes xifres de forma molt ràpida. Per això van introduir els logaritmes que en aquella època treballaven a partir de taules. En aquest enllaç pots llegir un exemple de com fer càlculs amb moltes xifres a partir de taules de logaritmes.

Avui dia, tot i que ja disposem de potent tecnologia, els logaritmes encara són molt útils per canviar escales per aquesta transformació de productes en sumes. En el món actual tenim diversos conceptes que es mesuren amb escales logarítmiques, per exemple:

    •  la intensitat d'un terratrèmol,
    • el PH d'una substància,
    • la intensitat del so....

En aquest lliurament aprendreu a treballar amb les propietats dels logaritmes que també us serviran per resoldre equacions exponencials.

És important que entenguem la notació que es fa servir. En general es fa constar la base del logaritme posant-la com a subíndex loga , però hi ha dos casos especials:

  • el logaritme decimal (en base 10). En aquest cas, en general no posarem el 10 i sobre-entendrem que es tracta del log decimal log space b equals space log subscript 10 space end subscript b
  • logaritme neperià (en base e). Aquest té una notació especial i en lloc de log escriurem ln.


Primers exemples

l o g subscript 2 space 8 space

    Per definició tenim

               log subscript 2 space 8 space equals x space space space left right double arrow space 2 to the power of x equals 8

        o sigui: a què hem d'elevar 2 perquè ens doni 8? ... resposta: 3

              log subscript 2 space 8 space equals x space space space left right double arrow space 2 to the power of x equals 8 space space space space space space space space space space space space space space space space space space space space space space space space space space space space 2 to the power of x equals 2 cubed space space space rightwards double arrow space space x equals 3   

                                                          box enclose space log subscript 2 space 8 equals 3 end enclose                                                       

l o g subscript blank 100 space

 Ja hem dit que si no s'indica base, és base 10

 Per tant, volem saber a què elevem 10 perquè ens doni 100?... resposta: 2

              log space 100 space equals x space space space left right double arrow space 10 to the power of x equals 100 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space 10 to the power of x equals 2 squared space space space rightwards double arrow space space x equals 2   

                                                               box enclose space log subscript blank 100 equals 2 end enclose                             

l o g subscript 3 space open parentheses 1 over 9 close parentheses space 

   

          log subscript 3 space open parentheses 1 over 9 close parentheses space equals x space space space left right double arrow space 3 to the power of x equals 1 over 9 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space 3 to the power of x equals 1 over 3 squared equals 3 to the power of negative 2 end exponent space space space rightwards double arrow space space x equals negative 2 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space box enclose log subscript 3 space open parentheses 1 over 9 close parentheses equals negative 2 end enclose

Ús dels logaritmes per resoldre algunes equacions exponencials.

Farem servir logaritmes quan treballem amb equacions on la incògnita "x" és un exponent. Equacions del tipus a to the power of x equals b

En els apartat anteriors ja vam resoldre equacions del tipus 2x=16, equacions en què podem expressar els termes com a potència d'una mateixa base: 2x=24 . 

Ara els logaritmes ens permetran resoldre equacions exponencials on no tots els termes són potències d'una mateixa base. Per exemple:

                                                               2 to the power of x equals 23      

    Per resoldre aquesta equació aplicarem logaritmes i necessitarem usar la calculadora.


Com calculem els logaritmes amb calculadora?

En general totes les calculadores tenen dos tecles referides als logaritmes. "log" i "ln". Altres més modernes tenen també una tecla que permet fer directament logaritmes en qualsevol base.

"log" correspon a logaritmes en base 10  (com hem dit quan la base és 10, aquesta no es posa, cal sobre-entendre-la)

 "ln" correspon a logaritmes en base "e" que es coneixent com a logaritmes neperians, en honor al matemàtic del s.XVI John Napier

Segons el model de la teva calculadora la sintaxi a escriure pot ser diferent (consulta el manual de la teva), en genera serà

log + nombre = resultat però de vegades és al revès: nombre + log =

El mateix amb el logaritme neperià.

Prova amb la teva calculadora aquests resultats i esbrina quin és el funcionament del teu model:

log1000= 3

log 25= 1,39794

ln e =1

ln 100= 4,605170186

Si ens cal calcular logaritmes en altres bases (i no disposem de la tecla que ens els fa directament), farem servir la propietat de canvi de base que s'explica més endavant però que aquí ja indiquem:

       log subscript a b equals fraction numerator log subscript c b over denominator log subscript c a end fraction, per tant transformarem el logaritme de partida a un dels dos que tenim ( log en base 10 o el neperià).

       log subscript 5 10 equals fraction numerator log 10 over denominator log 5 end fraction equals fraction numerator 1 over denominator 0 comma 69897004 end fraction equals 1 comma 430676558... log subscript 5 10 equals fraction numerator ln 10 over denominator ln 5 end fraction equals fraction numerator 2 comma 302585093.. over denominator 1 comma 609437912.. end fraction equals 1 comma 430676558...

Logaritmes sense calculadores

Com s'ha dit, abans s'utilitzaven taules de logaritmes i les propietats dels logaritmes per calcular-los. Avui en dia és molt senzill amb la calculadora.

Malgrat això hauríeu de ser capaços de calcular qualsevol logaritme d'un nombre que és potència de la base a partir només de  la pròpia definició de logaritme. Es tracta de fer servir les propietats de les potències que per tant caldrà que repassar.

Això només es podrà fer en cas que la b sigui potència de a: log subscript a b 

Veiem uns exemples:

Exemples
  • log subscript 2 cube root of 16 space equals 4 over 3 space space space space space space j a space q u e space space space space space cube root of 16 equals cube root of 2 to the power of 4 end root equals 2 to the power of 4 over 3 end exponent
  • log space 0 apostrophe 0001 space equals negative 4 space space space space space space j a space q u e space space space space 0 apostrophe 0001 space equals 1 over 10000 equals 1 over 10 to the power of 4 equals 10 to the power of negative 4 end exponent
  • log subscript 1 third end subscript space 243 space equals negative 5 space space space space space j a space q u e space 243 equals 3 to the power of 5 equals fraction numerator 1 over denominator begin display style 1 over 3 to the power of 5 end style end fraction equals fraction numerator 1 over denominator begin display style 3 to the power of negative 5 end exponent end style end fraction equals open parentheses 1 third close parentheses to the power of negative 5 end exponent

Propietats dels logaritmes

Com s'ha vist, la definició de logaritme està molt lligada a les potències, per tant les seves propietats també.

En aquesta taula es recullen les principals propietats que s'han d'estudiar i aplicar de forma rigorosa.

Tot logaritme té una expressió equivalent en forma de potència 


                     box enclose space space space space log subscript a b equals c space space space space left right double arrow space space space b equals a to the power of c space space space space space space space end enclose


a partir d'aquesta relació s'obtenen les següents propietats:  


                        box enclose table row cell log subscript a 1 equals 0 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space end cell row cell log subscript a space a equals 1 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space end cell row cell log subscript a left parenthesis b times c right parenthesis equals log subscript a b plus log subscript a c end cell row cell log subscript a open parentheses b over c close parentheses equals log subscript a b minus log subscript a c space space end cell row cell log subscript a open parentheses b to the power of c close parentheses equals c times log subscript a b space space space space space space space space space space space space end cell end table end enclose

Com aplicar aquestes propietats?

 log subscript 2 5 plus log subscript 2 3 equals log subscript 2 left parenthesis 5 times 3 right parenthesis log subscript 2 5 minus log subscript 2 3 equals log subscript 2 5 over 3 3 log subscript 2 5 equals log subscript 2 5 cubed

 2 times ln space 3 space plus space ln space 5 space equals ln space left parenthesis 3 squared times 5 right parenthesis   recordem que ln és el logaritme neperià (logaritme en base e)

 ln space 3 space plus space ln space 5 space minus space ln space 2 space equals ln space open parentheses fraction numerator 3 times 5 over denominator 2 end fraction close parentheses

          


Errades habituals

Les errades més freqüents són degudes a una mala utilització de les propietats dels logaritmes. Per tant cal estudiar bé les propietats certes i no "inventar-ne" de noves.

Són incorrectes les següents igualtats:

down diagonal up diagonal strike l o g subscript a x space times l o g subscript a y equals l o g subscript a left parenthesis x plus y right parenthesis l o g subscript a x space times l o g subscript a y equals l o g subscript a left parenthesis x y right parenthesis fraction numerator l o g subscript a x over denominator l o g subscript a y end fraction space equals l o g subscript a left parenthesis x minus y right parenthesis fraction numerator l o g subscript a x over denominator l o g subscript a y end fraction space equals l o g subscript a left parenthesis x over y right parenthesis end strike

Exemples:
  • log space x times left parenthesis x plus 1 right parenthesis space not equal to log space x space times log space left parenthesis x plus 1 right parenthesis
  • log space a over b not equal to fraction numerator log space a space over denominator log space b end fraction
  • log space 0 space not equal to space 0 space space space left parenthesis log space 0 space space space space N O thin space E X I S T E I X right parenthesis
  • log left parenthesis x plus 3 x cubed right parenthesis not equal to log space x space plus space log space x cubed

Equacions logarítmiques

Les equacions logarítmiques són aquelles en què les incògnites estan afectades per un logaritme.

Per exemple:

log left parenthesis x minus 2 right parenthesis plus log left parenthesis x plus 4 right parenthesis equals log left parenthesis 2 minus x right parenthesis

Per tal de resoldre-les cal tenir presents les propietats dels logaritmes que s'han enunciat abans.


Com resoldre les equacions logarítmiques?

Els passos per resoldre una equació logarítmica són els següents:

  1. Arreglar l'equació de manera que només quedi un únic logaritme (de la mateixa base) a cada membre. Per poder fer això cal utilitzar les propietats dels logaritmes. Sovint cal fer les següents transformacions:
    • Expressar un nombre com a logaritme    (per exemple 3=log 103=log 1000)
    • Expressar una suma de logaritmes com a únic logaritme (per exemple «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»log«/mi»«mi»x«/mi»«mo»§#160;«/mo»«mo»+«/mo»«mi»log«/mi»«mo»§#160;«/mo»«mo»(«/mo»«mi»x«/mi»«mo»+«/mo»«mn»3«/mn»«mo»)«/mo»«mo»=«/mo»«mi»log«/mi»«mo»§#160;«/mo»«mo»(«/mo»«mi»x«/mi»«mo»(«/mo»«mi»x«/mi»«mo»+«/mo»«mn»3«/mn»«mo»)«/mo»«mo»)«/mo»«/math» )
    • Expressar una resta de logaritmes com a únic logaritme (per exemple «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»log«/mi»«mi»x«/mi»«mo»§#160;«/mo»«mo»-«/mo»«mi»log«/mi»«mo»§#160;«/mo»«mo»(«/mo»«mi»x«/mi»«mo»+«/mo»«mn»3«/mn»«mo»)«/mo»«mo»=«/mo»«mi»log«/mi»«mo»§#160;«/mo»«mfrac»«mi»x«/mi»«mrow»«mi»x«/mi»«mo»+«/mo»«mn»3«/mn»«/mrow»«/mfrac»«/math» )
    • Expressar com a únic logaritme una multiplicació d'un nombre per un logaritme (per exemple «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn»2«/mn»«mi»log«/mi»«mo»§#160;«/mo»«mo»(«/mo»«mi»x«/mi»«mo»+«/mo»«mn»3«/mn»«mo»)«/mo»«mo»=«/mo»«mi»log«/mi»«mo»§#160;«/mo»«mo»(«/mo»«mi»x«/mi»«mo»+«/mo»«mn»3«/mn»«msup»«mo»)«/mo»«mn»2«/mn»«/msup»«/math»  )
  2. Treure els logaritmes de manera que ens queda un equació sense logaritmes. Això és pot fer degut a que la funció logarítmica «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»f«/mi»«mo»(«/mo»«mi»x«/mi»«mo»)«/mo»«mo»=«/mo»«msub»«mi»log«/mi»«mi»a«/mi»«/msub»«mi»x«/mi»«/math» és bijectiva des del conjunt (0,+∞) fins al (-∞,+∞) i per tant si «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»log«/mi»«mi»a«/mi»«/msub»«mi»x«/mi»«mo»=«/mo»«msub»«mi»log«/mi»«mi»a«/mi»«/msub»«mi»y«/mi»«mo»§#160;«/mo»«mo»§#8660;«/mo»«mi»x«/mi»«mo»=«/mo»«mi»y«/mi»«/math»
  3. Comprovar les solucions obtingudes substituint en l'equació inicial. Tenir present que no tenen sentit els logaritmes de valors negatius o 0.
  4. Descartar les solucions falses i quedar-nos amb les vàlides.
Exemple 1:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathcolor=¨#00007F¨»2«/mn»«mi mathcolor=¨#00007F¨»l«/mi»«mi mathcolor=¨#00007F¨»o«/mi»«mi mathcolor=¨#00007F¨»g«/mi»«mi mathcolor=¨#00007F¨»x«/mi»«mo mathcolor=¨#00007F¨»§#160;«/mo»«mo mathcolor=¨#00007F¨»=«/mo»«mn mathcolor=¨#00007F¨»3«/mn»«mo mathcolor=¨#00007F¨»+«/mo»«mi mathcolor=¨#00007F¨»l«/mi»«mi mathcolor=¨#00007F¨»o«/mi»«mi mathcolor=¨#00007F¨»g«/mi»«mfrac mathcolor=¨#00007F¨»«mi»x«/mi»«mn»10«/mn»«/mfrac»«mspace linebreak=¨newline¨/»«mi»log«/mi»«msup»«mi»x«/mi»«mn»2«/mn»«/msup»«mo»§#160;«/mo»«mo»=«/mo»«mi»log«/mi»«mo»§#160;«/mo»«mn»1000«/mn»«mo»+«/mo»«mi»log«/mi»«mfrac»«mi»x«/mi»«mn»10«/mn»«/mfrac»«mspace linebreak=¨newline¨/»«mi»log«/mi»«msup»«mi»x«/mi»«mn»2«/mn»«/msup»«mo»§#160;«/mo»«mo»=«/mo»«mi»log«/mi»«mo»§#160;«/mo»«mfenced»«mrow»«mn»1000«/mn»«mo»§#183;«/mo»«mfrac»«mi»x«/mi»«mn»10«/mn»«/mfrac»«/mrow»«/mfenced»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mspace linebreak=¨newline¨/»«mi»A«/mi»«mi»r«/mi»«mi»a«/mi»«mo»§#160;«/mo»«mi»t«/mi»«mi»r«/mi»«mi»a«/mi»«mi»i«/mi»«mi»e«/mi»«mi»m«/mi»«mo»§#160;«/mo»«mi»e«/mi»«mi»l«/mi»«mi»s«/mi»«mo»§#160;«/mo»«mi»log«/mi»«mi»a«/mi»«mi»r«/mi»«mi»i«/mi»«mi»t«/mi»«mi»m«/mi»«mi»e«/mi»«mi»s«/mi»«mspace linebreak=¨newline¨/»«msup»«mi»x«/mi»«mn»2«/mn»«/msup»«mo»§#160;«/mo»«mo»=«/mo»«mn»1000«/mn»«mo»§#183;«/mo»«mfrac»«mi»x«/mi»«mn»10«/mn»«/mfrac»«mo»§#8594;«/mo»«msup»«mi»x«/mi»«mn»2«/mn»«/msup»«mo»=«/mo»«mn»100«/mn»«mi»x«/mi»«mspace linebreak=¨newline¨/»«msup»«mi»x«/mi»«mn»2«/mn»«/msup»«mo»-«/mo»«mn»100«/mn»«mi»x«/mi»«mo»=«/mo»«mn»0«/mn»«mo»§#8594;«/mo»«mi»x«/mi»«mo»(«/mo»«mi»x«/mi»«mo»-«/mo»«mn»100«/mn»«mo»)«/mo»«mo»=«/mo»«mn»0«/mn»«mo»§#8594;«/mo»«mfenced open=¨{¨ close=¨¨»«mtable columnalign=¨left¨»«mtr»«mtd»«menclose notation=¨updiagonalstrike¨»«mi»x«/mi»«mo»=«/mo»«mn»0«/mn»«/menclose»«mo»§#160;«/mo»«mo»§#160;«/mo»«mo»§#160;«/mo»«mi»S«/mi»«mi»o«/mi»«mi»l«/mi»«mi»u«/mi»«mi»c«/mi»«mi»i«/mi»«mi»§#243;«/mi»«mo»§#160;«/mo»«mi»f«/mi»«mi»a«/mi»«mi»l«/mi»«mi»s«/mi»«mi»a«/mi»«mo»§#160;«/mo»«mi»j«/mi»«mi»a«/mi»«mo»§#160;«/mo»«mi»q«/mi»«mi»u«/mi»«mi»e«/mi»«mo»§#160;«/mo»«mi»log«/mi»«mo»§#160;«/mo»«mn»0«/mn»«mo»§#160;«/mo»«mo»§#8708;«/mo»«/mtd»«/mtr»«mtr»«mtd»«menclose notation=¨box¨»«mo»§#160;«/mo»«mi»x«/mi»«mo»=«/mo»«mn»100«/mn»«mo»§#160;«/mo»«/menclose»«/mtd»«/mtr»«/mtable»«/mfenced»«/math»

Exemple 2:

«math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mn mathcolor=¨#00007F¨»2«/mn»«mi mathcolor=¨#00007F¨»l«/mi»«mi mathcolor=¨#00007F¨»o«/mi»«mi mathcolor=¨#00007F¨»g«/mi»«mo mathcolor=¨#00007F¨»§#160;«/mo»«mi mathcolor=¨#00007F¨»x«/mi»«mo mathcolor=¨#00007F¨»-«/mo»«mn mathcolor=¨#00007F¨»2«/mn»«mi mathcolor=¨#00007F¨»l«/mi»«mi mathcolor=¨#00007F¨»o«/mi»«mi mathcolor=¨#00007F¨»g«/mi»«mo mathcolor=¨#00007F¨»(«/mo»«mi mathcolor=¨#00007F¨»x«/mi»«mo mathcolor=¨#00007F¨»+«/mo»«mn mathcolor=¨#00007F¨»1«/mn»«mo mathcolor=¨#00007F¨»)«/mo»«mo mathcolor=¨#00007F¨»=«/mo»«mn mathcolor=¨#00007F¨»0«/mn»«mo mathcolor=¨#00007F¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mi mathcolor=¨#191919¨»R«/mi»«mi mathcolor=¨#191919¨»e«/mi»«mi mathcolor=¨#191919¨»s«/mi»«mi mathcolor=¨#191919¨»o«/mi»«mi mathcolor=¨#191919¨»l«/mi»«mi mathcolor=¨#191919¨»u«/mi»«mi mathcolor=¨#191919¨»c«/mi»«mi mathcolor=¨#191919¨»i«/mi»«mi mathcolor=¨#191919¨»§#243;«/mi»«mo mathcolor=¨#191919¨»:«/mo»«mspace linebreak=¨newline¨/»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»l«/mi»«mi mathcolor=¨#191919¨»o«/mi»«mi mathcolor=¨#191919¨»g«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«msup mathcolor=¨#191919¨»«mi mathcolor=¨#191919¨»x«/mi»«mn»2«/mn»«/msup»«mo mathcolor=¨#191919¨»-«/mo»«mi mathcolor=¨#191919¨»l«/mi»«mi mathcolor=¨#191919¨»o«/mi»«mi mathcolor=¨#191919¨»g«/mi»«mo mathcolor=¨#191919¨»(«/mo»«mi mathcolor=¨#191919¨»x«/mi»«mo mathcolor=¨#191919¨»+«/mo»«mn mathcolor=¨#191919¨»1«/mn»«msup mathcolor=¨#191919¨»«mo mathcolor=¨#191919¨»)«/mo»«mn»2«/mn»«/msup»«mo mathcolor=¨#191919¨»=«/mo»«mn mathcolor=¨#191919¨»0«/mn»«mo mathcolor=¨#191919¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»l«/mi»«mi mathcolor=¨#191919¨»o«/mi»«mi mathcolor=¨#191919¨»g«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«msup mathcolor=¨#191919¨»«mi mathcolor=¨#191919¨»x«/mi»«mn»2«/mn»«/msup»«mo mathcolor=¨#191919¨»=«/mo»«mi mathcolor=¨#191919¨»l«/mi»«mi mathcolor=¨#191919¨»o«/mi»«mi mathcolor=¨#191919¨»g«/mi»«mo mathcolor=¨#191919¨»(«/mo»«mi mathcolor=¨#191919¨»x«/mi»«mo mathcolor=¨#191919¨»+«/mo»«mn mathcolor=¨#191919¨»1«/mn»«msup mathcolor=¨#191919¨»«mo»)«/mo»«mn»2«/mn»«/msup»«mspace linebreak=¨newline¨/»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mspace linebreak=¨newline¨/»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»A«/mi»«mi mathcolor=¨#191919¨»r«/mi»«mi mathcolor=¨#191919¨»a«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»t«/mi»«mi mathcolor=¨#191919¨»r«/mi»«mi mathcolor=¨#191919¨»a«/mi»«mi mathcolor=¨#191919¨»i«/mi»«mi mathcolor=¨#191919¨»e«/mi»«mi mathcolor=¨#191919¨»m«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»e«/mi»«mi mathcolor=¨#191919¨»l«/mi»«mi mathcolor=¨#191919¨»s«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»log«/mi»«mi mathcolor=¨#191919¨»a«/mi»«mi mathcolor=¨#191919¨»r«/mi»«mi mathcolor=¨#191919¨»i«/mi»«mi mathcolor=¨#191919¨»t«/mi»«mi mathcolor=¨#191919¨»m«/mi»«mi mathcolor=¨#191919¨»e«/mi»«mi mathcolor=¨#191919¨»s«/mi»«mspace linebreak=¨newline¨/»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«msup mathcolor=¨#191919¨»«mi mathcolor=¨#191919¨»x«/mi»«mn»2«/mn»«/msup»«mo mathcolor=¨#191919¨»=«/mo»«mo mathcolor=¨#191919¨»(«/mo»«mi mathcolor=¨#191919¨»x«/mi»«mo mathcolor=¨#191919¨»+«/mo»«mn mathcolor=¨#191919¨»1«/mn»«mrow mathcolor=¨#191919¨»«msup»«mo»)«/mo»«mn»2«/mn»«/msup»«mo»§#8594;«/mo»«msup»«mi»x«/mi»«mn»2«/mn»«/msup»«mo»=«/mo»«msup»«mi»x«/mi»«mn»2«/mn»«/msup»«mo»+«/mo»«mn»1«/mn»«mo»+«/mo»«mn»2«/mn»«mi»x«/mi»«/mrow»«mspace linebreak=¨newline¨/»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mn mathcolor=¨#191919¨»0«/mn»«mo mathcolor=¨#191919¨»=«/mo»«msup mathcolor=¨#191919¨»«mi mathcolor=¨#191919¨»x«/mi»«mn»2«/mn»«/msup»«mo mathcolor=¨#191919¨»-«/mo»«msup mathcolor=¨#191919¨»«mi mathcolor=¨#191919¨»x«/mi»«mn»2«/mn»«/msup»«mo mathcolor=¨#191919¨»+«/mo»«mn mathcolor=¨#191919¨»1«/mn»«mo mathcolor=¨#191919¨»+«/mo»«mn mathcolor=¨#191919¨»2«/mn»«mi mathcolor=¨#191919¨»x«/mi»«mspace linebreak=¨newline¨/»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mn mathcolor=¨#191919¨»0«/mn»«mo mathcolor=¨#191919¨»=«/mo»«mn mathcolor=¨#191919¨»1«/mn»«mo mathcolor=¨#191919¨»+«/mo»«mn mathcolor=¨#191919¨»2«/mn»«mi mathcolor=¨#191919¨»x«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#8594;«/mo»«mo mathcolor=¨#191919¨»-«/mo»«mn mathcolor=¨#191919¨»1«/mn»«mo mathcolor=¨#191919¨»=«/mo»«mn mathcolor=¨#191919¨»2«/mn»«mi mathcolor=¨#191919¨»x«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#8594;«/mo»«mi mathcolor=¨#191919¨»x«/mi»«mo mathcolor=¨#191919¨»=«/mo»«mo mathcolor=¨#191919¨»-«/mo»«mfrac mathcolor=¨#191919¨»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»Q«/mi»«mi mathcolor=¨#191919¨»u«/mi»«mi mathcolor=¨#191919¨»e«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»n«/mi»«mi mathcolor=¨#191919¨»o«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»§#233;«/mi»«mi mathcolor=¨#191919¨»s«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»v«/mi»«mi mathcolor=¨#191919¨»§#224;«/mi»«mi mathcolor=¨#191919¨»l«/mi»«mi mathcolor=¨#191919¨»i«/mi»«mi mathcolor=¨#191919¨»d«/mi»«mi mathcolor=¨#191919¨»a«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»p«/mi»«mi mathcolor=¨#191919¨»e«/mi»«mi mathcolor=¨#191919¨»r«/mi»«mi mathcolor=¨#191919¨»q«/mi»«mi mathcolor=¨#191919¨»u«/mi»«mi mathcolor=¨#191919¨»§#232;«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»log«/mi»«mfenced mathcolor=¨#191919¨»«mrow»«mo»-«/mo»«mfrac»«mn»1«/mn»«mn»2«/mn»«/mfrac»«/mrow»«/mfenced»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#160;«/mo»«mo mathcolor=¨#191919¨»§#8708;«/mo»«mspace linebreak=¨newline¨/»«mi mathcolor=¨#191919¨»P«/mi»«mi mathcolor=¨#191919¨»e«/mi»«mi mathcolor=¨#191919¨»r«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»tan«/mi»«mi mathcolor=¨#191919¨»t«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»a«/mi»«mi mathcolor=¨#191919¨»q«/mi»«mi mathcolor=¨#191919¨»u«/mi»«mi mathcolor=¨#191919¨»e«/mi»«mi mathcolor=¨#191919¨»s«/mi»«mi mathcolor=¨#191919¨»t«/mi»«mi mathcolor=¨#191919¨»a«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»e«/mi»«mi mathcolor=¨#191919¨»q«/mi»«mi mathcolor=¨#191919¨»u«/mi»«mi mathcolor=¨#191919¨»a«/mi»«mi mathcolor=¨#191919¨»c«/mi»«mi mathcolor=¨#191919¨»i«/mi»«mi mathcolor=¨#191919¨»§#243;«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»n«/mi»«mi mathcolor=¨#191919¨»o«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»t«/mi»«mi mathcolor=¨#191919¨»§#233;«/mi»«mo mathcolor=¨#191919¨»§#160;«/mo»«mi mathcolor=¨#191919¨»s«/mi»«mi mathcolor=¨#191919¨»o«/mi»«mi mathcolor=¨#191919¨»l«/mi»«mi mathcolor=¨#191919¨»u«/mi»«mi mathcolor=¨#191919¨»c«/mi»«mi mathcolor=¨#191919¨»i«/mi»«mi mathcolor=¨#191919¨»o«/mi»«mi mathcolor=¨#191919¨»n«/mi»«mi mathcolor=¨#191919¨»s«/mi»«/math»

Consulta el següent document on trobaràs més exemples d'equacions exponencials resoltes.

Equacions logarítmiques resoltes

Més exemples de resolució d'equacions logaritmiques

bold italic l bold italic o bold italic g subscript bold 2 bold italic x bold equals bold 3

  Apliquem:     log subscript straight a straight b equals straight c space left right double arrow space straight a to the power of straight c equals straight b    

                         log subscript 2 x equals 3 space space space left right double arrow space x equals 2 cubed

   Per tant,   bold italic x bold equals bold 8


bold italic l bold italic o bold italic g bold space bold italic x bold equals bold minus bold 2  

  (recordem que quan no es posa base és logaritme decimal (en base 10)

   Procedint com a en l'exemple anterior tenim: 

                    x equals 10 to the power of negative 2 end exponent space space space rightwards arrow space x equals 1 over 10 squared equals bold 0 bold comma bold 01

bold italic l bold italic o bold italic g subscript bold 2 open parentheses bold x close parentheses bold plus bold italic l bold italic o bold italic g subscript bold 2 open parentheses bold 3 close parentheses bold equals bold italic l bold italic o bold italic g subscript bold 2 open parentheses bold 5 close parentheses

Aplicant la propietat    log subscript a left parenthesis b times c right parenthesis equals log subscript a b plus log subscript a c

                         tenim:   l o g subscript 2 open parentheses straight x close parentheses plus l o g subscript 2 open parentheses 3 close parentheses equals l o g subscript 2 open parentheses 3 x close parentheses

 Per tant, ens queda: 

          log subscript 2 open parentheses 3 x close parentheses equals log subscript 2 open parentheses 5 close parentheses space space space rightwards arrow 3 x equals 5 space space space rightwards arrow space space bold italic x bold equals bold 5 over bold 3


bold italic l bold italic o bold italic g subscript bold 3 open parentheses bold x close parentheses bold plus bold italic l bold italic o bold italic g subscript bold 3 open parentheses bold 5 close parentheses bold equals bold 2

   log subscript 3 open parentheses 5 x close parentheses equals 2 space space space space rightwards arrow space space 5 x equals 3 squared space space space rightwards arrow space bold space bold italic x bold equals bold 9 over bold 5


bold italic l bold italic o bold italic g open parentheses bold 2 bold x bold plus bold 1 close parentheses bold minus bold italic l bold italic o bold italic g open parentheses bold x close parentheses bold equals bold 3

Aplicant la propietat:        log subscript a open parentheses b over c close parentheses equals log subscript a b minus log subscript a c

           tenim:       l o g open parentheses 2 straight x plus 1 close parentheses minus l o g open parentheses straight x close parentheses equals log open parentheses fraction numerator 2 x plus 1 over denominator x end fraction close parentheses

per tant ens queda:

  log open parentheses fraction numerator 2 x plus 1 over denominator x end fraction close parentheses equals 3 space space space rightwards arrow space fraction numerator 2 x plus 1 over denominator x end fraction equals 10 cubed space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space 2 x plus 1 equals 1000 x space space rightwards arrow 998 x equals 1 space space rightwards arrow space bold italic x bold equals bold 1 over bold 998

bold italic l bold italic n bold space bold italic x bold space bold minus bold space bold italic l bold italic n bold space bold 5 bold equals bold 2 bold space

   ln open parentheses x over 5 close parentheses equals 2 space space ln open parentheses x over 5 close parentheses equals ln space e squared rightwards arrow space space x over 5 equals e squared space space rightwards arrow space bold italic x bold equals bold 5 bold italic e to the power of bold 2

 

bold 2 bold italic l bold italic o bold italic g bold left parenthesis bold italic x bold right parenthesis bold minus bold italic l bold italic o bold italic g open parentheses bold x bold minus bold 3 close parentheses bold equals bold 2

log left parenthesis x squared right parenthesis space minus space log space left parenthesis x minus 3 right parenthesis space equals 2

Usem una de les propietats de les potències

log open parentheses fraction numerator x squared over denominator x minus 3 end fraction close parentheses equals 2

Passem a potències aquesta expressió.

10 squared equals fraction numerator x squared over denominator x minus 3 end fraction

Aquesta és una equació de segon grau.

100 times left parenthesis x minus 3 right parenthesis space equals space x squared 100 x minus 300 space equals x squared 0 equals x squared minus 100 x plus 300 x equals fraction numerator negative left parenthesis negative 100 right parenthesis plus-or-minus square root of 100 squared minus 4 times 1 times 300 end root over denominator 2 times 1 end fraction equals fraction numerator 100 plus-or-minus square root of 8800 over denominator 2 end fraction equals fraction numerator 100 plus-or-minus 93.8 over denominator 2 end fraction x subscript 1 equals 96.9 x subscript 2 equals 3.1

Ara cal comprovar que les solucions són correctes, substituint en l'equació inicial

Si  x1 = 96.9    →   log left parenthesis 96.9 squared right parenthesis space minus space log space left parenthesis 96.9 minus 3 right parenthesis space equals 2     Correcte. Amb més decimals millor aproximació.

Si  x2 = 3.1     →    log left parenthesis 3.1 squared right parenthesis space minus space log space left parenthesis 3.1 minus 3 right parenthesis space equals 2          Correcte. Amb més decimals millor aproximació.

La solucions són     x1 = 96.9      i      x2 = 3.1 



Per què cal comprovar les solucions en una equació logarítmica?

Al igual que en les equacions irracionals i en les racionals, al passar d'una equació que té logaritmes (arrels o denominadors) a una que no en té, es poden introduir solucions falses, això vol dir que són solució de l'equació sense logaritmes però no de l'original.

És per això que un cop trobades les solucions possibles caldrà provar-les a l'equació inicial i descartar aquelles que no tenen sentit. Recordar que només es pot definir el logaritme de nombres positius estrictes.

Exemples

L e s space s o l u c i o n s space d e space l apostrophe e q u a c i ó space space x squared space equals 1000 times x over 10 space space s ó n space x equals 0 space i space x equals 100 P e r ò space e n space c a n v i space X equals 0 space n o space é s space s o l u c i ó space d e space l apostrophe e q u a c i ó log x squared space equals log space open parentheses 1000 times x over 10 close parentheses space space space j a space q u e space s u b s t i t u ï n t space e n space q u a l s e v o l space d e l s space d o s space m e m b r e s comma space p e r space e x e m p e space e n space e l space s e g o n space space l a space x space p e r space 0 space o b t e n i m space log space open parentheses 1000 times 0 over 10 close parentheses space equals log space 0 space space q u e space there does not exist space P e r space tan t space v e i e m space q u e space e n c a r a space q u e space a equals b space n o space s e m p r e space e s space c o m p l i r à space q u e space log space a equals log space b. N o m é s space s e r à space c e r t space s i space a equals b space s ó n space n o m b r e s space p o s i t i u s. space

Funcions logarítmiques

Una funció logarítmica és aquella que té la variable independent aplicada a un logaritme.

f left parenthesis x right parenthesis equals log subscript a left parenthesis x right parenthesis

En cas que la a=10 (logaritme decimal) no escrivim la base i per tant escrivim només f left parenthesis x right parenthesis equals log left parenthesis x right parenthesis 

En cas que la base sigui el nombre e, li diem logaritme neperià i la notació sol ser f left parenthesis x right parenthesis equals ln left parenthesis x right parenthesis


Característiques de la funció logaritme

f left parenthesis x right parenthesis equals log subscript a left parenthesis x right parenthesis space a greater than 0

  • El seu domini són tots els reals estrictament positius: D o m space f left parenthesis x right parenthesis equals open curly brackets x greater than 0 close curly brackets equals open parentheses 0 comma plus infinity close parentheses.
  • El recorregut és tot R.
  • Si la base a> 1 la funció és estrictament creixent.
  • Si la base a compleix 0<a<1 la funció logaritme és estrictament decreixent.
  • El punt de tall amb l'eix d'abscisses és (1,0)
  • Té una asímptota vertical en x=0, és a dir quan la x tendeix a 0 (sempre per la part positiva) la funció s'acosta a plus infinity o negative infinity segons el valor de la a.
Càlcul de dominis
Quan calculem dominis de funcions logarítmiques s'ha d'imposar que la funció a qui se li aplica el logaritme sigui estrictament positiva.
S i space f left parenthesis x right parenthesis equals log subscript a left parenthesis g left parenthesis x right parenthesis right parenthesis rightwards double arrow D o m space f left parenthesis x right parenthesis equals open curly brackets x vertical line g left parenthesis x right parenthesis greater than 0 close curly brackets
Exemples
  • f left parenthesis x right parenthesis equals log subscript 2 left parenthesis x plus 3 right parenthesis. Aquesta funció està definida si x+3> 0 i per tant D o m space f left parenthesis x right parenthesis equals left curly bracket x element of R vertical line x greater than negative 3 right curly bracket equals left parenthesis negative 3 comma plus infinity right parenthesis

  • g left parenthesis x right parenthesis equals ln left parenthesis x ² right parenthesis. Aquesta funció estarà definida si x²>0 per tant
    D o m space g left parenthesis x right parenthesis equals straight real numbers minus left curly bracket 0 right curly bracket equals left parenthesis negative infinity comma 0 right parenthesis union left parenthesis 0 comma plus infinity right parenthesis

  • h left parenthesis x right parenthesis equals log left parenthesis x ² minus 1 right parenthesis. Aquesta funció estarà definida si x²-1>0 per tant caldrà estudiar aquesta inequació.
    Resolem l'equació x squared minus 1 equals 0 left right double arrow x ² equals 1 left right double arrow x equals plus-or-minus 1
    Aquests dos punts separen la recta real en tres intervals: left parenthesis negative infinity comma negative 1 right parenthesis semicolon space left parenthesis negative 1 comma space plus 1 right parenthesis semicolon space left parenthesis 1 comma plus infinity right parenthesis
    Provarem un punts senzill interior a cada interval per saber quan és positiu:
    -Provem un punt interior a left parenthesis negative infinity comma negative 1 right parenthesis, per exemple el -2 :   (-2)² -1 = 4-1>0   interessa l'interval.
    -Provem un punt interior a left parenthesis negative 1 comma 1 right parenthesis, per exemple el 0 :   (0)² -1 = -1<0   no interessa l'interval.
    -Provem un punt interior a left parenthesis negative 1 comma plus infinity right parenthesis, per exemple el 2 :   (2)² -1 = 4-1>0   interessa l'interval.
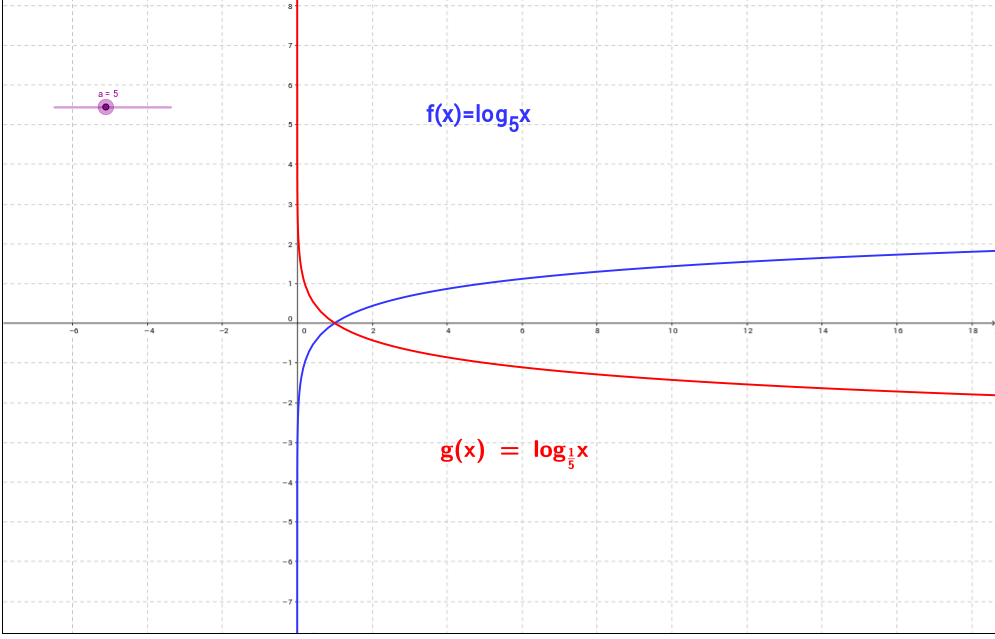
    Conclusió: D o m space h left parenthesis x right parenthesis equals straight real numbers minus left curly bracket 0 right curly bracket equals left parenthesis negative infinity comma negative 1 right parenthesis union left parenthesis 1 comma plus infinity right parenthesis


Com varia el gràfic d'una funció logarítmica en funció de la seva base?

La relació és total:

Si la base "a" de la funció logarítmica  f left parenthesis x right parenthesis equals log subscript a x és un nombre major que 1 o està entre 0 i 1 el gràfic és molt diferent:


Observeu a les imatges superiors que per bases més grans a 1 la funció és creixent (esquerra) ve de menys infinit i va creixent indefinidament tallant a l'eix de les x en el punt (1,0).

En el cas de bases entre 0 i 1 el gràfic és decreixent (dreta) ve de menys infinit i va decreixent indefinidament tallant a l'eix de les x en el punt (1,0).

Si cliqueu damunt la imatge inferior accedireu a un applet fet amb Geogebra per Marta Bachs on podreu observar com varia el gràfic de la funció logaritme en moure el valor de la a a partir del punt lliscant que veureu a l'esquerra. Observeu que teniu dibuixat el gràfic per bases del logaritme ai pels seus inversos  1 divided by a. Fixeu-vos bé en les característiques dels gràfics en cada cas i extraieu-ne conclusions.


Relació entre la funció exponencial i la funció logarítmica.

Clicant damunt la imatge accedireu a un applet fet amb geogebra per Julio Sánchez que us permetrà veure de forma interactiva la relació entre la funció exponencial i logarítmica de la mateixa base. Una funció és la inversa de l'altre.

Moveu el punt lliscant a i observeu com canvia el gràfic de les dues funcions quan la a és més petita que 1 o més gran que 1.

Comproveu les característiques de les funcions exponencials i logarítmiques explicades en els capítols anteriors.

Observeu que les dues gràfiques són sempre simètriques respecte a la recta y=x perquè són funcions inverses.


Problemes aplicats

Les funcions exponencials i logarítmiques són habituals en molts estudis de diferents disciplines.

Això fa que la principal aplicació sigui la resolució de problemes.

Comencem amb un exemple senzill.


Suposem que la població d'un tipus de bacteri creix segons la següent funció :  f left parenthesis t right parenthesis space equals 10 times 2 to the power of t over 3 end exponenton t és el temps en hores.

a) A l'inici, quants bacteris hi h ?

b) I passat 1 dia, quants bacteris hi haurà?

c) I passats 3 dies?

d) Quant de temps ha de transcórrer per tal que hi hagi el triple de bacteris que a l'inici?

Resposta:

a) Inici, correspon a t= 0. Basta fer la substitució en la funció:

f left parenthesis 0 right parenthesis space equals 10 times 2 to the power of 0 over 3 end exponent equals space 10 times 2 to the power of 0 equals 10 space b a c t e r i s

b) 1 dia = 24 h, correspon a t=24

f left parenthesis 24 right parenthesis space equals 10 times 2 to the power of 24 over 3 end exponent equals space 10 times 2 to the power of 8 equals 2560 space b a c t e r i s

c) 3 dies = 3 ·24 h = 72 h

f left parenthesis 72 right parenthesis space equals 10 times 2 to the power of 72 over 3 end exponent equals space 10 times 2 to the power of 24 equals 167772160 space b a c t e r i s

d) Cal plantejar l'equació : f left parenthesis t right parenthesis space equals 10 times 2 to the power of t over 3 end exponent equals space 30  i resoldre-la

10 space times space 2 to the power of t over 3 end exponent equals 30 P a s s e m space e l space 10 space a l space s e g o n space m e m b r e space d e space l apostrophe e q u a c i ó space 2 to the power of t over 3 end exponent equals 30 over 10 space 2 to the power of t over 3 end exponent equals 3 P a s s e m space a space l o g a r i t m e s colon t over 3 equals space log subscript 2 left parenthesis 3 right parenthesis A m b space l apostrophe a j u t space d e space l a space c a l c u l a d o r a colon space log subscript 2 left parenthesis 3 right parenthesis space equals fraction numerator log left parenthesis 3 right parenthesis over denominator log left parenthesis 2 right parenthesis end fraction equals 1.5849 t over 3 equals 1.5849 S apostrophe a ï l l a space &quot; t &quot; t equals 1.5849 space times space 3 t equals 4.75 space h o r e s

Problema aplicat: medicament en sang

Quan un malalt pren un medicament, aquest s'absorbeix i a partir d'un cert moment  l'organisme comença a eliminar-lo, de manera que la seva concentració en sang C(t) (mesurada en mg/l) va disminuint segons aquesta funció: bold italic C bold left parenthesis bold italic t bold right parenthesis bold equals bold 0 bold comma bold 05 bold times bold italic e to the power of bold minus bold 0 bold comma bold 3 bold times bold t end exponent essent t el temps mesurat en minuts.


Es demana:

a) Quina és la concentració de medicament en sang inicial (t=0)?

b) Quina concentració en sang té el malalt després d'un quart d'hora?

c) Quant de temps ha de transcórrer perquè la concentració de medicament en sang sigui el 10% de la inicial?

Resolució:
a)
La concentració inicial la tindrà quan t=0, és a dir hem de calcular la imatge de 0 per la funció i per tant només ens cal substituir t=0 a la funció i operar.
C left parenthesis 0 right parenthesis equals 0 comma 05 times e to the power of negative 0 comma 3 times 0 end exponent equals 0 comma 05 times e to the power of 0 equals 0 comma 05 times 1 equals 0 comma 05
La concentració inicial de medicament a la sang és de 0,05mg/l.

 
b)
La concentració passat un quart d'hora la tindrem a l'instant 15, per tant hem de calcular la imatge de 15 per la funció C(t) substituint t per 15.
C left parenthesis 15 right parenthesis equals 0 comma 05 times e to the power of negative 0 comma 3 times 15 end exponent equals 0 comma 05 times e to the power of negative 4 comma 5 end exponent equals 0 comma 05 times 0 comma 011108996 equals 5 comma 55 times 10 to the power of negative 4 end exponent
 
La concentració després de 15 minuts de medicament a la sang és d'aproximadament 5,55·10-4 mg/l.

c)
Calculem primer el 10% de la concentració inicial que serà 0,005.
Ara coneixem la concentració i hem de calcular el temps, és a dir, caldrà trobar l'antiimatge de 0,005 per la funció C(t) resolen l'equació exponencial que en resulta.
  0 comma 005 equals 0 comma 05 times e to the power of negative 0 comma 3 times t end exponent

Hem de treballar amb aquesta equació fins a aconseguir aïllar la t. Haurem de fer servir les tècniques explicades en la resolució d'equacions exponencials.
fraction numerator 0 comma 005 over denominator 0 comma 05 end fraction equals e to the power of negative 0 comma 3 times t end exponent 0 comma 1 equals e to the power of negative 0 comma 3 times t end exponent space space a p l i q u e m space ln space a l s space d o s space m e m b r e s ln left parenthesis 0 comma 1 right parenthesis equals ln left parenthesis e to the power of negative 0 comma 3 times t end exponent right parenthesis ln left parenthesis 0 comma 1 right parenthesis equals negative 0 comma 3 t rightwards arrow t equals negative fraction numerator ln left parenthesis 0 comma 1 right parenthesis over denominator 0 comma 3 end fraction almost equal to 7 comma 67528 space m i n almost equal to 7 space m space i space 40 space s
S'aconsegueix un 10% de concentració de medicament a la sang transcorreguts uns 7 minuts i 40 segons aproximadament.

Problema aplicat : el virus d'Ebola

Durant la darrera epidèmia d'Ebola , es va considerar que, sense cap intervenció, el virus es propagava augmentant en un 3% diari el nombre d'infectats. Suposem que en certa població hi ha a dia d'avui 25 persones infectades.


Es demana:

a) Escriu l'expressió de la funció f(x) que ens dóna el nombre de persones infectades en passar els dies.

b) Quantes persones infectades hi haurà el 10è dia?

c) Aplicant certes mesures sanitàries el nombre d'infectats comença a disminuir segons la funció  bold italic g bold left parenthesis bold italic x bold right parenthesis bold equals bold 1000 bold times bold left parenthesis bold 0 bold comma bold 95 bold right parenthesis to the power of bold x. Es considera que l'epidèmia està controlada si el nombre de malalts és de 10 o menys persones. A partir de quin dia (un cop aplicades les mesures sanitàries) es podrà donar per controlada l'epidèmia? 

Resolució:

a) Escriu l'expressió de la funció f(x) que ens dóna el nombre de persones infectades en passar els dies.

Tenim que a l'inici hi ha 25 infectats.

després d'un dia tindrem 25·1,03

després de dos dies  25·1,03·1,03, és a dir 25·(1,03)2

i generalitzant després de x dies el nombre d'infectats ve donat per la funció box enclose f left parenthesis x right parenthesis equals 25 times left parenthesis 1 comma 03 right parenthesis to the power of x end enclose

b) Quantes persones infectades hi haurà el 10è dia?

Per saber el nombre d'infectats el 10è dia només hem de substituir la x per 10 a la funció anterior.f left parenthesis 10 right parenthesis equals 25 times open parentheses 1 comma 03 close parentheses to the power of 10 equals 33 comma 59.

Tenint en compte que parlem d'infectats estaríem entre 33 i 34 infectats.


c) Aplicant certes mesures sanitàries el nombre d'infectats comença a disminuir segons la funció  g left parenthesis x right parenthesis equals 1000 times left parenthesis 0 comma 95 right parenthesis to the power of x. Es considera que l'epidèmia està controlada si el nombre de malalts és de 10 o menys persones. A partir de quin dia (un cop aplicades les mesures sanitàries) es podrà donar per controlada l'epidèmia? 

En aquest cas ens caldrà resoldre la següent equació:

10 equals 1000 times left parenthesis 0 comma 95 right parenthesis to the power of x

operem fins a aïllar la x

open parentheses 0 comma 95 close parentheses to the power of x equals 10 over 1000 equals 0 comma 01 a p l i q u e m space l o g space a l s space d o s space m e m b r e s l o g open parentheses 0 comma 95 close parentheses to the power of x equals space l o g space 0 comma 01 equals negative 2 x times l o g open parentheses 0 comma 95 close parentheses equals space minus 2 x equals fraction numerator negative 2 over denominator l o g open parentheses 0 comma 95 close parentheses end fraction almost equal to 89 comma 78

És a dir podrem donar l'epidèmia com a controlada a partir del 90è dia un cop iniciades les mesures sanitàries.