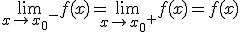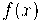Límits
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques I (Bloc 2) ~ gener 2020 |
| Llibre: | Límits |
| Imprès per: | Usuari convidat |
| Data: | dimecres, 26 de juny 2024, 07:48 |
Descripció
Resum
1. Límit d'una funció en un punt
Definició
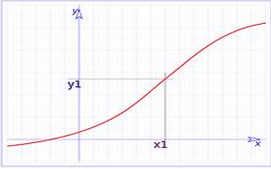
El límit d'una funció f(x) quan x tendeix a a és on s'aproxima la funció quan les x s'aproximen al valor de a.
Exemple
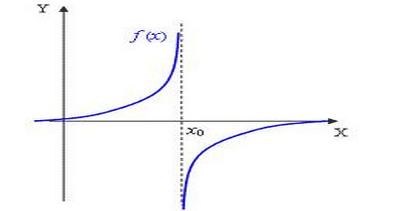
Veiem que en aquest cas quan els valors de x s'aproximen a 0, els valors de la funció no s'aproximen a cap nombre real sinó que es fan tan grans com vulgem. En aquest cas el límit és ∞
| x | 0'1 | 0'01 | 0'001 | 0'0001 | |
| f(x) | 10 | 100 | 1000 | 10000 |
2. Límit en l'infinit d'una funció
Definició
. El límit d'una funció f(x) quan x tendeix a +∞ és on s'aproxima la funció quan prenem valors de x cada vegada més grans
. El límit d'una funció f(x) quan x tendeix a -∞ és on s'aproxima la funció quan prenem valors de x cada vegada més petits
Exemple
| x | 10 |
100 | 1000 | 10000 |
|
|
| f(x) | 0'1 |
0'01 | 0'001 | 0'0001 |
| x | -10 |
-100 | -1000 | -10000 |
|
|
| f(x) | -0'1 |
-0'01 | -0'001 | -0'0001 |
En aquest cas , podem escriure:
Per calcular el que hem de fer en primer lloc és substituir, en l'expressió de la funció, la x per a i fer els càlculs. Ens podem trobar amb tres casos :
1. Que el resultat doni un nombre i per tant aquest serà el valor del límit
Exemples
a)
b)
c)
2.
Que ens doni una indeterminació. En els altres apartats d'aquest llibre expliquem com resoldre algunes d'aquestes indeterminacions.
Exemple
el límit encara NO està calculat.
En aquest cas, hem de resoldre aquesta indeterminació (veure apartat Resolució indeterminació 0/0 )
3.
Que ens doni una expressió de
on k és un nombre real, i en aquest cas el límit serà infinit
.
El signe de l'infinit dependrà del signe de k i del 0 . Si necessitem saber el signe de l'infinit podeu anar a l'apartat Límits laterals
Exemple
Límits laterals
De vegades, quan calculem el valor d'un límit ens interessa distingir si ens acostem al punt per la seva dreta o per la seva esquerra i això ho anomenem límits laterals.
Sempre podem fer els límits laterals, però és imprescindible fer-ho quan la funció té, en el punt de tendència, un canvi de definició o bé és un punt que no pertany al domini.
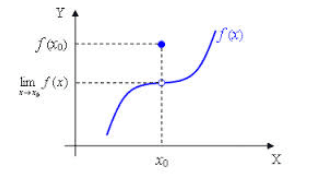
Farem servir la següent notació per referir-nos al límit o límits laterals d'una funció en un punt p.
Si fem un límit i arribem a una expressió de tipus caldrà mirar el "signe" d'aquest 0 substituint l'expressió que dóna el 0 per valors molt propers a x=a.
El resultat pot ser un nombre molt proper a 0 però positiu (0+) o bé negatiu (0-).
En aquest cas dependrà també del valor de k per decidir el signe del resultat final. Per exemple:
Exemples
Potser amb aquest resultat tenim prou. Si volem determinar el signe d'aquest infinit, hem de fer els límits laterals:
. Límit per la dreta:
. Límit per l'esquerra:
Substituïm en l'expressió x-1 la x per un nombre molt proper a 1 per la seva dreta per exemple 1'000001.
veiem que dóna un nombre molt proper a zero i positiu (0+) i per tant ja podem dir .
Substituïm en l'expressió x2-1 la x per un nombre molt proper a 1 per la seva esquerra per exemple 0'99999.
veiem que dóna un nombre molt proper a zero i negatiu (0-) i per tant ja podem dir .
Substituïm en l'expressió la x per un nombre molt proper a -2 per la seva esquerra per exemple -2'000001.
veiem que dóna un nombre molt proper a zero i negatiu (0-) i per tant ja podem dir .
Substituïm en l'expressió la x per un nombre molt proper a -2 per la seva dreta per exemple -1'99999.
veiem que dóna un nombre molt proper a zero i positiu (0+) i per tant ja podem dir .
Càlcul de límits gràficament
Si tenim el gràfic d'una funció, per calcular límits només haurem de veure a què tendeix el gràfic quan ens acostem al punt.
Serà important si el límit és a la dreta o a l'esquerra del punt.
Per entendre-ho cal tenir en compte que a les funcions definides a trossos els punts oberts vol dir que no pertanyen a la funció, en canvi els punts plens sí que es consideren del gràfic de la funció.
Veiem algun exemple

En aquest gràfic la imatge de 2, f(2) és 3 observem que el punt ple és (2, 3) en canvi (2, 0) és un punt obert que vol dir que no pertany a la funció.

A partir d'aquest gràfic calculem:
Límit en el punt 2
A què tendeix el gràfic quan ens acostem a 2 per la dreta?Observeu a la imatge que si ens acostem per l'esquerra del 2 (1,9; 1,99; etc) tendim a 0,
En canvi si ens apropem a 2 per la dreta, és a dir per valors una mica més gran que 2 (2,1; 2,01; 2,001, etc) tendim a 3.
Com aquests dos límits no coincideixen deduïm que no existeix el límit de la funció en el punt 2.

|

|
|---|
Límit en el punt -3
Si ens acostem per l'esquerra al punt -3, observem que el gràfic creix indefinidament, per tant va cap a + infinit.
En canvi si ens acostem a -3 per la dreta, el gràfic va cap a baix indefinidament, tendeix a - infinit.
Això ho expressem així:
A
En els altres punts el límit sí que existeix, observem que la funció no fa cap altre discontinuïtat i per tant no importa per quin costat ens acostem al punt, perquè coincideix.
Per exemple
Límit en el punt 0
Podríem fer el mateix en qualsevol altre punt.
Càlcul de límits
Amb els límits de funcions són vàlides les mateixes operacions que s'han indicat amb el límit de successions.
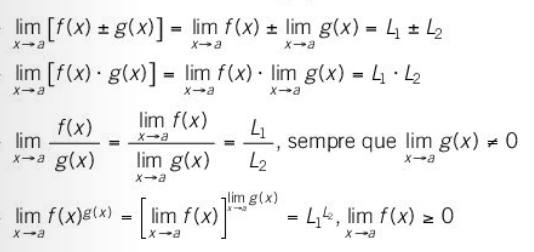
En calcular límits ens podem trobar amb situacions que es resolen
immediatament i altres (que anomenem indeterminacions) que requereixen
d'un estudi més detallat per poder donar el resultat final.
Aquestes són les principals casuístiques que ens podem trobar (k es refereix a un valor constant finit):
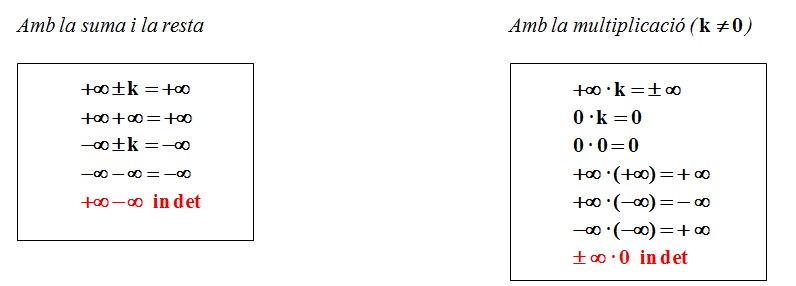


La paraula indet significa en aquest cas "No està clar el resultat, podria donar qualsevol cosa"
Les indeterminacions requereixen com hem dit d'un estudi més detallat per saber el resultat. I cada tipus d'indeterminació té les seves tècniques per resoldre's. En treballarem algunes.
Límits de funcions polinòmiques
En general, si coneixem l'expressió algebraica de la funció per calcular-ne el límit en un punt substituirem la funció en el punt.
Anem a veure com calcular límits segons el tipus de funció que treballem. Comencem amb els polinomis i el seu cas particular les constants.
Funció constant
Si tenim una funció de tipus
amb k un nombre real qualsevol exiteix límit de la funció en qualsevol punt (també a infinit) i el límit sempre val k.
Exemple

|
|---|
Funció polinòmica
Els límits a infinit i a menys infinit de les funcions polinòmiques sempre serà +∞ o -∞
. Caldrà estudiar amb cura
el signe.
Podem resumir-ho d'aquesta manera:
</p>
<p>
</p>
<p>(cal recordar el signe de les potències amb base negativa i la llei dels signes).</p>
<h5>Exemple <br></h5>
<p>
</p>
<p>Calculem el límit en els punts x=2 i x=-1</p>
<p>
</p>Ara calculem els límits a
<br>
Observem que el coeficient de grau màxim de la funció és -1 i el grau del polinomi és 3, per tant senar.
<br>
<p>Volem calcular els límits:</p>
<p>Comencem per fer una taula per saber la tendència de la funció:</p>
<p>Primer posem valors de "x" que van creixent cap a l'infinit, i estudiem què passa amb les seves imatges, i observem que obtenim valors molt petits , ja que són negatius.</p>
<p>A la taula de la dreta fem el mateix però amb valors negatius cada vegada més petits.
<br>
</p>
<table style="margin-left: 90px;" border="0">
<tbody style="margin-left: 90px;">
<tr style="margin-left: 90px;">
<td style="border-style: solid; border-width: 1px; margin-left: 90px;" scope="col"></td>
<td style="border-color: #000000; border-style: solid; border-width: 1px; margin-left: 90px;" scope="col">





Límits de funcions racionals
Les funcions racionals són les formades per la divisió de dos polinomis 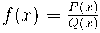
on
on
Límits en un punt
Per fer els límits en un punt p en principi substituirem la funció en el punt.
- Si dóna un valor finit aquest serà el límit.
- En cas que doni
el límit serà
en funció del signe de la k i del 0. Caldrà fer els límits laterals.
- Si dóna
es tracta d'una indeterminació que caldrà resoldre. Haurem de factoritzar numerador i denominadors, simplificar i després tornar a fer el límit. Les treballarem una mica més endavant.
Exemples
calculem els límits en els punts 3, 5 i -1.
com dividim per 0, serà
. Caldrà estudiar els límits laterals per saber-ho.
Com els dos límits laterals prenen valors diferents, el límit en 5 no existeix.
Aprendrem més endavant a resoldre aquest tipus d'indeterminacions.
Límits a infinit
Per fer límits a només ens fixarem en el terme de grau més alt de cada polinomi i aquests termes
ens donaran el límit. És a dir ens fixarem en
del polinomi P(x) i en
del
polinomi Q(x)
El límit final dependrà del grau de la següent manera:
El signe de l'infinit caldrà estudiar-lo amb detall seguint el que s'ha comentat amb les funcions polinòmiques i la regla dels signes.
Exemples
el signe és negatiu perquè el numerador és negatiu i denominador positiu
Resolució de la indeterminació 0/0
El cas més usual d'indeterminació del tipus 0/0 és quan la funció és racional, és a dir una divisió entre dos polinomis.
En aquest cas procedim a factoritzar els dos polinomis, simplificar i finalment tornar a fer el límit
Exemple 1
Exemple 2
Exemple 3
Exemple 4
Límits d'una potència de dues funcions
Aplicant les propietats de límit, si tenim
Calcularem els límits de f i de g. Llavors si
Exemples
Límits de funcions definides a trossos
Per calcular el límit d'una funció en x=a podem distingir entre dos casos:
- Que x = a no sigui un punt de trencament de la funció
- Que x = a sigui un punt de trencament de la funció (punt on la funció canvia d'expressió)
Cas 1:
En aquest cas per calcular el límit sols cal que fem el límit utilitzant l'expressió de la funció que correspon a l 'interval on pertany x=a
Cas 2 :
En aquest cas l'expressió de la funció a utilitzar canvia si fem el límit per l'esquerra o per la dreta. Per tant hem de fer els límits laterals en x=a.
Sols existirà el límit de la funció en x=a en el cas que aquests límits laterals coincideixin. I en aquest cas
Exemple
Calculem els límits en x=-5, -3, -2, 0, 0'5, 1 i 1'5
En x = -5
En x = -3 hi ha un punt de trencament de la funció per tant cal calcular els límits laterals
En x = -2
En x = 0 no hi ha imatge i és un punt de trencament de la funció per tant cal calcular els límits laterals
Compte!!: que un valor de x no sigui del domini no implica que no tingui límit. En aquest cas en x=0 no té límit però no té res a veure en que x=0 no sigui del domini
En x = 0'5
En x =1 hi ha un trencament de la funció per tant cal calcular els límits laterals
En x = 1'5
Continuïtat d'una funció
Una funció és contínua si la poden dibuixar sense aixecar el llapis del paper. En els punts on sigui necessari aixecar el llapis de paper serà discontínua.
Si de la funció es coneix la gràfica és fàcil respondre a les preguntes: És una funció contínua? I si és discontínua, en quins punts és discontínua? Quins tipus de discontinuïtat té la funció?
Observeu aquests exemples:
| Funció contínua | Funció discontínua en x0 amb discontinuïtat evitable |
|
Aquesta funció és contínua ja que: |
Aquesta funció no és contínua. Ell punt (x0, f(x0)) fa que sigui discontínua. Els límits laterals (les dues branques) coincideixen. |
| Funció discontínua en x0 amb discontinuïtat de salt | Funció discontínua en x0 amb discontinuïtat asimptòtica |
|
Aquesta funció no és contínua. Les dues branques no es troben. Això fa que la funció sigui discontínua. I ell punt (x0, f(x0)) està situat sobre una de les dues branques. Hi ha un salt. |
Aquesta funció no és contínua. Ell punt (x0, f(x0)) no existeix, no és del domini de la funció. Les dues branques no es troben i s'enfilen cap al ∞. Tot això fa que sigui discontínua. |
Però en la majoria de les ocasions volem saber si la funció és contínua sense tenir la seva representació gràfica. És més, necessitem saber la continuïtat de la funció per tal de trobar de manera més fàcil la seva gràfica.
És per això que estudiarem la continuïtat de la funció o bé a partir de la seva gràfica o bé a partir de l'equació i amb l'ajut dels límits.
Què hem de fer per estudiar en quins punts la funció és discontínua?
Bàsicament ens fixarem en punts on la funció no estigui definida (que no pertanyin al domini) o punts on canviï la definició de la funció (funcions definides a trossos).
En aquests punts farem el següent estudi:
- calcularem els dos límits laterals.
- calcularem el valor de la funció en el punt
- Si les tres coses existeixen i coincideixen la funció serà contínua.
Continuïtat i tipus de discontinuïtat
Les funcions polinòmiques, exponencials, racionals, logarítmiques són contínues en tot el seu domini.
Com hem dit abans els punts que caldrà estudiar seran els punts frontera del domini i també els punts on les funcions definides a trossos canvien la seva definició.
Per a que una funció sigui contínua en un punt cal que passin aquestes tres coses:
- Existeixi
- Existeixi el límit
i pren valor finit (per calcular aquest límit habitualment farem els límits laterals i comprovarem que coincideixin)
- El límit coincideixi amb el valor de la funció en el punt.
Si alguna d'aquestes tres coses falla direm que la funció presenta una discontinuïtat en el punt.
Les discontinuïtats seran de diferent tipus segons quina d'aquestes tres coses falla.
Discontinuïtat evitable
Tindrem aquest tipus de discontinuïtat en el cas que existeixi el límit de la funció en el punt a (existeixen els dos límits laterals, són finits i coincideixen), però no coincideixi amb f(a) o bé no existeix f(a).
Es diu evitable justament perquè es podria evitar si definíssim la funció de manera que

Observant aquestes imatges veiem que si definíssim f(a) de manera que completes el punt obert del gràfic aconseguiríem que aquesta es pogués dibuixar sense aixecar el llapis del paper, aconseguiríem per tant que fos una funció contínua.
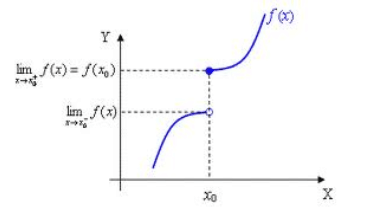
Discontinuïtat de salt finit
Tindrem una discontinuïtat d'aquest tipus en cas que els límits laterals en el punt existeixin però valguin valors diferents.
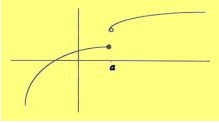
Observem en el gràfic d'exemple, que presenta un salt en el punt a. Si ens acostem a a per la dreta o per l'esquerra es tendeix a valors diferents.
Discontinuïtat de salt infinit
Si els límits laterals d'una funció en un punt existeixen, però almenys un pren valor infinit direm que tenim una discontinuïtat de salt infinit.
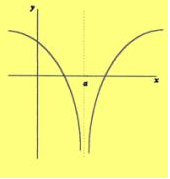
Aquest tipus de discontinuïtat indiquen l'existència d'una asímptota vertical x=a almenys per un dels dos costats, és per això que aquest tipus de discontinuïtat també es coneix com discontinuïtat asimptòtica.