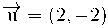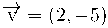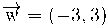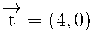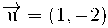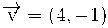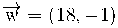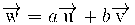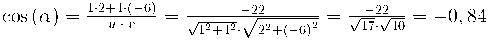Resum conceptes bàsics: complexos i vectors
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques I (Bloc 1) ~ gener 2020 |
| Llibre: | Resum conceptes bàsics: complexos i vectors |
| Imprès per: | Usuari convidat |
| Data: | divendres, 17 de maig 2024, 06:49 |
Descripció
Resum conceptes bàsics del lliurament 4 de Matemàtiques 1 Bloc 1: temes: vectors i complexos.
Origen dels nombres complexos
Fins a principis del s. XVI, els matemàtics quan resolien equacions i arribaven a arrels quadrades negatives, senzillament deien que l'equació no tenia solució. Això però, suposava un obstacle i a partir de la segona meitat del s.XVI es va idear la manera
de poder treballar amb aquestes arrels.
Per la necessitat de donar sentit a les arrels negatives es definiren els nombres complexos Es va començar ideant una nova unitat que es va anomenar la unitat imaginària i es denota amb la lletra
Els nombres complexos tenen una estructura de cos, això vol dir que se'ls pot definir les operacions suma + i multiplicació * i aquestes compleixen una sèrie de propietats (com ja passa amb els nombres reals).
En moltes branques de la ciència com la electrotècnia o la enginyeria l'ús dels nombres complexos és imprescindible. De moment però, en els següents capítols, veurem com expressar-los i operar amb ells.
Abans d'entrar en matèria, no et perdis aquest vídeo del canal Derivando on el matemàtic Eduardo Sánchez Cabezón t'ho explica d'una forma força amena.
Formes d'expressar un nombre complex
Un nombre complex és la suma d'un nombre real i un nombre imaginari, és a dir que conté la unitat imaginària Els nombres complexos els podrem expressar de diferents formes, bàsicament en forma binòmica i en forma polar. Com el mateix complexe es podrà expressar de les dues maneres serà important saber passar de l'una a l'altra i veure com es fan les operacions amb els dos tipus d'expressions.
Els complexos en forma binòmica, tal com diu la paraula s'expressen a partir d'un binomi de nombres reals
Els complexos en forma polar, s'expressen a partir de la seva situació en el pla i depenen d'un mòdul i un angle o argument
Anem a veureu amb més detall.
Forma binòmica d'un nombre complex
Un complex en forma binòmica s'expressa
Dos nombres complexos són iguals si tenen la mateixa expressió en forma binòmica, és a dir si són iguals les seves parts reals i les seves parts imaginàries.
Exemples:
-
és un complex amb part real 3 i part imaginària 2.
-
és un complex amb part real 4 i part imaginària -1. (Recordar que el coeficient 1 no es posa)
-
és un complex amb part real 0 i part imaginària 2.(Aquest tipus de nombres es solen anomenar imaginaris purs)
-
és un complex amb part real 5 i part imaginària 0. Observeu per tant, que els nombres reals són un cas particular de nombre complex amb part imaginària 0, per això diem que els nombres complexos contenen els reals.
Conjugat i oposat d'un complex
Donat un complex
Exemples:
-
el conjugat és
i l'oposat és
-
el conjugat és
i l'oposat és
-
el conjugat és
i l'oposat és
-
el conjugat és
i l'oposat és
Operacions en forma binòmica
- Suma i resta fer sumes i restes amb complexos en forma binòmica equival a sumar o restar les parts reals entre elles i les parts imaginàries entre elles.
- Potències de la
.
Observem que passa amb les potències de laa partir de la seva definició
:
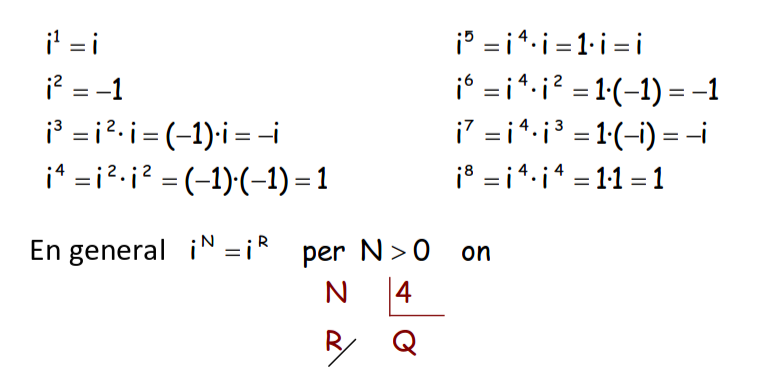
És a dir, si hem de fer una potència gran de la i, dividirem l'exponent entre 4 i ens quedarem amb el residu (que sempre serà un nombre entre 0 i 3).
Per exemple, com podem expressar
? Comencem agafant l'exponent 105 i el dividim entre 4.
Observem que el quocient és 26 i el residu 1, per tant això vol dir que
- Multiplicar nombres complexos per multiplicar dos complexos escrits en forma binòmica, cal procedir de la mateixa manera que fem quan multipliquem expressions algebraiques, tenint en compt el que
. S'aplica la propietat distributiva, es fa servir la definició de la unitat imaginària i finalment es simplifica deixant un sol terme real i un d'imaginari.
- Dividir complexos en forma binòmica, multipliquem numerador i denominador pel conjugat d'aquest últim. Després, es fan operacions en el numerador i en el denominador; fins aconseguir que al denominador només
apareguin nombres reals.
- Multiplicar un complex per un escalar real
Exemples:
Considerem els següents complexos :En aquest document: Complexos en forma binòmica trobareu més exemples resolts.
Exemples en forma binòmica
Desenvolupem alguns exemples d'operacions en forma binòmica:observa que hem aplicat la igualtat notable el quadrat d'una suma.
observeu que hem fet servir la igualtat notable suma per diferència
Als document Complexos en forma binòmica del recurs Llibre i documents trobaràs molts més exemples d'operacions amb complexos. Consulta'ls.
Exercici 1: Arrel
Sabem que és una arrel cúbica d'un complexe
a) Trobar z i expressar-lo en forma binòmica.
b) Calcular les altres dues arrels cúbiques de z.
Procediment
a) Si
Per tant
Expressem aquest complexe en forma binòmica :
b) Per trobar les altres dues arrels cúbiques de z tenim dues opcions:
- o bé calcular les tres arrels cúbiques de z i llavors apareixerà la que ja sabem i les altres dues.
- o bé, sabent que totes les arrels cúbiques d'un complex tenen el mateix mòdul i els angles difereixen en
.
Aplicant aquest segon mètode que és més curt tenim que les arrels cúbiques de z són:la que ja tenim.
Exercici 2: potències
Donat els complexos
Per fer la potència en forma polar, cal pensar que una potència és un cas particular de producte, per tant
Exercici 3: càlcul
Com ha de ser un nombre complex si en multiplicar-lo per Anem fent pas a pas el que diu l'enunciat.
Primer el multipliquem per
Ara li sumem
Ara imposem que aquest resultat sigui un nombre real tal com demana l'enunciat. Això passarà si la part imaginària és 0.
Per exemple:
- a=0 b=- 1/2, per tant serveix el complex
- a=1 b= -2, per tant serveix el complex
Exercici 4: càlcul
Troba un complex Forma 1
Podríem fer-ho com a l'exercici anterior, és a dir operant la part esquerra i després igualant els dos membres les parts reals i les parts imaginàries entre elles. Proposem una segona forma per fer-ho.Forma 2
Podem aïllar directament laAra passem a fer el càlcul que tenim indicat:
Equacions de segon grau amb solucions complexes
Quan treballem sobre reals, diem que una equació de segon grau no té solució si el discriminant és negatiu.
Sobre el cos dels nombres complexos, les equacions de segon grau sempre tenen solució. Fem servir que
Així per tant .
Si el discriminant és negatiu l'equació de segon grau té dues solucions complexes conjugades.
Exemple
Trobar les solucions de l'equació
Apliquem la fórmula corresponent
Observa que les dues solucions són conjugades una de l'altre.
Equacions biquadrades amb solucions complexes
De la mateixa manera, les equacions biquadrades passen a tenir sempre 4 solucions, potser complexes.
Recordem que una equació biquadrada és de tipus
Per resoldre-la fem el canvi t=x2 obtenint . Aquesta
equació tindrà dues solucions
t1 i t2 potser complexes.
I llavors fent l'arrel quadrada de cadascuna d'aquestes solucions, trobarem les 4 solucions de l'equació inicial. Cal tenir present que si t1 i t2 són complexes, caldrà aplicar les tècniques de radicació dels complexos per acabar.
Exemple
fem el canvi t=x² obtenint:
.
Resolem aquesta equació:
Ara caldria fer les dues arrels quadrades d'aquests dos complexes per a trobar les 4 solucions de l'equació inicial.
Vectors
Algunes magnituds queden completament determinades a partir d'un nombre real i les unitats adients, per exemple la massa, la temperatura, la longitud, etc. Aquestes magnituds les coneixem com escalars.
Altres requereixen més característiques per a la seva total determinació: el mòdul, la direcció i el sentit. Aquestes magnituds es coneixen com vectorials i la força, el desplaçament o la velocitats en són exemples.
En aquest tema ens ocuparem de les magnituds vectorials, que es representen a partir d'un vector.
Un vector fix ve determinat per dos punts: l'origen i l'extrem. Les components d'un vector fix, es calculen restant les coordenades de l'extrem menys les de l'origen. En general quan ens referim a un vector escriurem una fletxeta a dalt.

- el mòdul és la longitud del segment que el determina.
- la direcció ve donada per la recta que aquest vector determina
- el sentit ve indicat per l'origen del vector (el punt A) i l'extrem (el punt B).

Dos vectors són equipol·lents si tenen el mateix mòdul, direcció i sentit.
Un vector lliure és el conjunt format per tots els vectors fixos equipol·lents a un vector donat.
Exemple 1
a) Representa en uns eixos de coordenades els punts A=(0,-3) i B=(5,2), també el vector a)

Exemple 2
A la següent imatge tens assenyalats 5 punts sobre els eixos. Escriu les seves coordenades i les components del vector 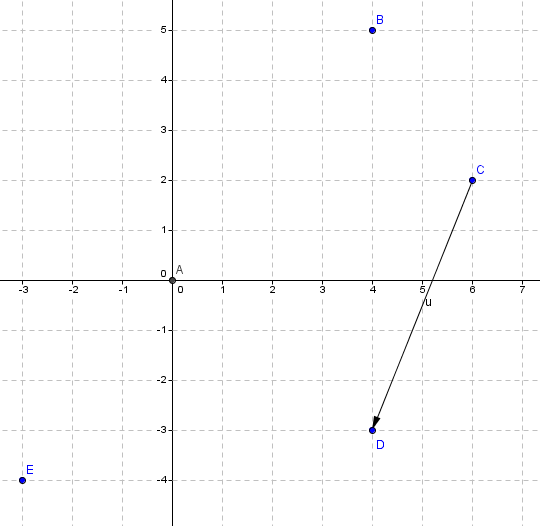
Resposta: A=(0,0) ; B=(4,5) ; C=(6,2) ; D=(4,-3) ; E=(-3,-4)
Operacions amb vectors
Podem operar amb vectors gràficament dibuixant-los o analíticament operant amb components.
- Suma

-
Producte per escalar real
En multiplicar un vector per un nombre real k obtenim un nou vector amb la mateixa direcció, el mòdul queda multiplicat pel valor absolut de l'escalar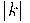 (més llarg o més curt) i el sentit és el mateix si el nombre era positiu o bé
oposat si el nombre era negatiu.
(més llarg o més curt) i el sentit és el mateix si el nombre era positiu o bé
oposat si el nombre era negatiu.


Exercici: operacions amb vectors
| Donats els següents vectors: | |

|
|
a) Identifica cada vector dibuixat amb les seves components:
El vector 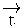 correspon al vector 1
correspon al vector 1
El vector 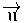 correspon al vector 2
correspon al vector 2
El vector 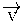 correspon al vector 3
correspon al vector 3
El vector 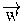 correspon al vector 4
correspon al vector 4
b) Calcula les components del vector
c) Calcula les components del vector
Combinació lineal de vectors
Anomenem combinació lineal de vectors a tota expressió del tipus: Exemple
Si i
el vector
podem dir que és combinació lineal de
perquè es compleix que
.
Comprovem-ho amb components:
Dependència i indepèndencia de vectors
Dos vectors del pla són independents si .
De fet, donats dos vectors del pla, aquests seran independents sempre que no siguin múltiples l'un de l'altre. En cas contrari direm que són dependents.
En resum, en el pla tenim:
Els vectors dependents del pla són vectors paral·lels.

u i 2u són dependents. u i -u també son dependents |
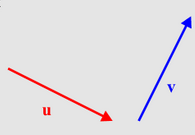
u i v són independents |
|---|
Així per exemple els vectors i
són dependents perquè
En canvi i
són independents perquè no és possible escriure
com a múltiple de
.
Observeu
Per tant no té solució i això ens garanteix que són vectors independents del pla.
Exercici combinació lineal de vectors
Donats els vectors :
Escriu el darrer com a combinació lineal dels dos primers.
Recordem que això significa que hem de trobar a i b nombres reals complint
Es tractarà doncs de plantejar i resoldre un sistema d'equacions amb les incògnites a i b.
(18 ,-1) = a(1, -2) + b(4, -1)
Separem les dues components de la igualtat
1ª component: 18= a +4b
2ª component -1= -2a-b
Observem que ja tenim un sistema lineal de dues equacions i dues incògnites, només cal resoldre'l per qualsevol dels mètodes treballats en lliuraments anteriors.
Utilitzem per exemple el mètode de substitució:
Aïllem la a de la primera equació: a= 18-4b (*)
Substituïm aquest valor a la segona equació i treballem fins a poder aïllar la b:
-1 = -2(18-4b)-b ----> -1= -36 + 8b - b ----> -1+36= 8b-b -----> 7b= 35----> b= 5
Tornem a (*) per trobar la a.
a= 18 - 4·5= 18-20= -2
Aquests sistema té com solució : a=-2 i b= 5 i ja tenim la combinació lineal que busquem
Resposta: La combinació lineal és la següent:
Angle entre dos vectors
Si es fa coincidir l'origen de dos vectors lliures, definim l'angle entre els dos vectors com el més petit entre els dos angles que es formen (α i 360o-α)

Producte escalar
El producte escalar
Càlcul del producte escalar amb components
Si coneixem les components dels dos vectors en base ortogonal (en general els vectors venen donats en base (1, 09 i (0,1) que ho és), el càlcul del producte escalar es limita a fer la suma del producte de les seves components:

Per exemple si:
el producte escalar de tots dos vectors es calcularia fent
Producte escalar d'un vector per ell mateix.
Observem que en aquest cas obtenim el mòdul al quadrat del vector.
Com calcular l'angle entre dos vectors?
Si coneixem el producte escalar entre dos vectors, i els seus mòduls, fàcilment podrem calcular l'angle que formen els dos vectors.
Partirem de la definició de producte escalar i aïllarem el cosinus. Un cop tinguem el cosinus, aplicant la funció arccos amb la calculadora trobarem l'angle.

Vectors perpendiculars
Diem que dos vectors són perpendiculars o ortogonals si formen un angle de 90⁰ (π/2 rad).
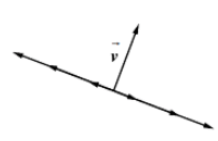
Exemple
Donat el vector amb components (3, 5). Trobeu cinc vectors ortogonals a ell.El que seria més senzill seria (-5, 3) (observeu que hem canviat l'ordre de les components i una d'elles de signe). A partir d'aquest només ens cal buscar múltiples si en volem més.
Els vectors (-5,3), (5, -3), (-10, 6), (-2.5, 1.5), (-15, 9) són ortogonals al primer. I seria molt fàcil trobar-ne més.
Vectors unitaris
Diem que un vector és unitari si el seu mòdul és 1. Donat un vector podem construir un vector de la mateixa direcció i sentit però unitari senzillament dividint-lo per la seva norma o mòdul.
Exemple
Donat el vector en calculem el seu mòdul.
Com el seu mòdul no és 1 aquest vector no és unitari.
Com podem trobar un vector de la mateixa direcció i sentit que unitari? Dividint les dues components per el mòdul obtingut.
seria un vector unitari de la mateixa direcció i sentit que
.
Exercicis resolts de producte escalar
Exercici 1
Calcular el producte escalar de dos vectors 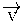 i
i 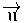 sabent que el primer té un mòdul de 3 el segon de 2,5 i formen un angle de 45o.
sabent que el primer té un mòdul de 3 el segon de 2,5 i formen un angle de 45o.
Aplicant la definició tenim :
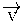 ·
· 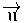 = 3 · 2,5 · cos(45o) = 3 · 2,5 · 0,71 = 5,325
= 3 · 2,5 · cos(45o) = 3 · 2,5 · 0,71 = 5,325
Exercici 2
Calculem el producte escalar dels vectors 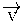 i
i 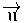 que tenen per components respectivament (8,1) i (-2, 7)
que tenen per components respectivament (8,1) i (-2, 7)
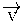 ·
· 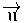 =8· (-2) + 1 · 7 = -16 + 7 = -9
=8· (-2) + 1 · 7 = -16 + 7 = -9
Exercici 3
Quin angle formen els vectors 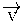 =(1,4) i
=(1,4) i 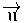 = (2,-6) ?
= (2,-6) ?
Com en coneixem les components podem calcular-ne el producte escalar i després el cosinus:
Ara amb la calculadora busquem quin angle té per cosinus -0,84
arc cos (-0,84)= 147.14⁰ (recordeu que això a la majoria de les calculadores es fa SHIFT COS -0,84 =
Obtenim α =147,14⁰
Dividir un segment en parts iguals
Considerem el segment determinat pels punts A=(a1, a2) i B=(b1, b2).
- Com trobar el punt M que divideix el segment en dues parts iguals?
- Com trobar els punts N i O que el divideixin en 3 parts iguals?
El primer que cal fer és trobar les components del vector
.
Si el punt M divideix el segment en dues parts iguals, tenim que

Si treballem en components i diem (m1, m2) a les coordenades del punt M, a partir de la igualtat vectorial assenyalada anteriorment tenim:
Igualem component a component i aïllem les m.
Si ara dividim el segment en tres parts iguals, la situació serà la següent:

I per tant si considerem els vectors que formen aquests punts tenim:
Això amb components ho podem escriure:
Per trobar el punt O es pot procedir de diverses maneres, per exemple:
Problema resolt 1: quadrilàter
Donat el quadrilàter: ABCD amb vèrtex A=(2,2); B=(4,0); C=(6,2) i D=(4,4), Es demana:
a) Justifiqueu raonadament que es tracta d'un quadrat.
b) Trobeu les
coordenades del punt M on es tallen les dues diagonals.
c) Calculeu l'àrea del quadrilàter.
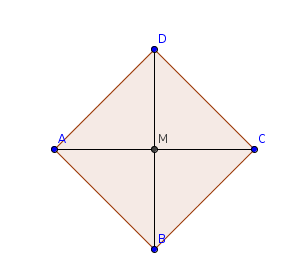
Per comprovar que el quadrilàter donat és un quadrat calcularem primer la mida dels quatre costats comprovant que són iguals.
- Calculem les components dels vectors que formen els quatre costats restant l'extrem menys l'origen i el mòdul de cada vector.
- Per veure que els 4 angles són de 90⁰ podem provar que els vectors que contenen els angles són perpendiculars entre sí, és a dir hem de veure que tenen producte escalar 0.
Procedim anàlogament amb la resta dels angles.
Angle
Angle
Angle
Si M=(x, y) tenim:
Treballem component a component:
4= 2x-4-----> 2x=8----->x=4
0= 2y-4-----> 2y=4----->y=2
El punt que busquem és
c) Per calcular l'àrea hem d'aplicar la fórmula de l'àrea d'un quadrat, és a dir costat x costat, on la mida del costat és el mòdul dels vectors calculats a l'apartat a).