Posa't a prova amb els problemes de Termodinàmica química (I)
Exercicis
1. La següent reacció correspon a la reacció de formació del gas metà.
C (grafit) + 2 H2 (g) → CH4 (g)
A partir de les dades entàlpiques de les reaccions següents, calculeu l'entalpia estàndard de formació del metà.
a- C (grafit) + O2 (g) → CO2 (g) ΔH° = -393,5 kJ
b- H2 (g) + 1/2 O2 (g) → H2O (l) ΔH° = -285,8 kJ
c- CH4 (g) + 2 O2 (g) → CO2 (g) + 2 H2O (l) ΔH° = -890,4 kJ
Solució:
La reacció de formació del gas metà s'obté a partir de la següents combinació d'eqüacions:
a + 2 · b ─ c
C (grafit) + O2 (g) → CO2 (g) ΔH°A = -393,5 kJ
2 x [ H2 (g) + 1/2 O2 (g) → H2O (l)] 2·ΔH°B= 2·(-285,8 kJ)
CO2 (g) + 2 H2O (l) → CH4 (g) + 2 O2 (g) - ΔH°C= -(-890,4 kJ)
Operem les equacions, segons la combinació anterior: a + 2 · b ─ c i simplifiquem:
C (grafit) + 2 H2 (g) + 2 O2 (g) + CO2 (g) + 2 H2O (l) →CH4 (g) +2 O2 (g) + CO2 (g) + 2 H2O (l)
Per tant:
ΔH° = ΔH°A + 2·ΔH°B ─ ΔH°C = -393,5 + 2·(-285,8) ─ (-890,4) = - 74,7 kJ
2. L'età es produeix per hidrogenació de l'acetilè, segon la reacció:
C2H2 (g) + 2H2 (g) → C2H6 (g) ΔH° =?
Calculeu la variació de l’entalpia de la reacció a partir dels valors de les energies d’enllaç:
ΔH°CΞC = 898,4 kJ/mol ; ΔH°C-C = 348,1kJ/mol; ΔH°C-H = 415,3 kJ/mol; ΔH°H-H = 436,4 kJ/mol.
Solució:
En la formació de l'età a partir de l'acetilè es trenca un enllaç C≡C, dos enllaços H-H i es formen 1 enllaç C-C i quatre enllaços C-H.
L’entalpia de la reacció serà:
ΔH° = Energia enllaços trencats – Energia d’enllaços formats =
= [1 ·ΔH°CΞC + 2 · ΔH°H-H ] ─ [1 · ΔH°C-C + 4 · ΔH°C-H ] =
= [1 · 898,4 kJ/mol + 2 · 436,4 ] ─ [1 · 348 + 4 · 415,3] = -238,1 kJ · mol-1
3. La reacció d'oxidació catalítica de l'amoníac és el punt de partida per a l'obtenció industrial de l'àcid nítric i es produeix segons l'equació:
4 NH3(g) + 5 O2(g) → 6 H2O(l) + 4 NO(g)
Calculeu l'entalpia estàndard d'aquesta reacció a partir de les dades de les entalpies estàndard de formació.
ΔH°f [NH3(g)] = -46,3 kJ · mol-1 ; ΔH°f[O2(g)] = 0
ΔH°f[NO(g)] = + 90,4 kJ · mol-1; ΔH°f[H2O(l)] = -285,8 kJ · mol-1
Solució:
Apliquem l'expressió:
ΔH°reacció = Σ n · ΔH°f productes - Σ n · ΔH°f reactius =
= 6· ΔH°f[H2O(l)] + 4 · ΔH°f[NO(g)] - 4 ΔH°f [NH3(g)] - 5 ΔH°f[O2(g)] =
(2,5 p) = 6 mols· ( -285,8 kJ · mol-1) + 4 · (+ 90,4 kJ · mol-1) - 4 (-46,3 kJ · mol-1) - 0 = - 1168 kJ
4. La següent reacció correspon a la cloració del metà.
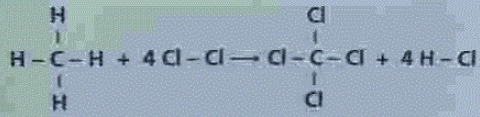
En la taula següent hi teniu dades d'energies mitjanes d'enllaç:
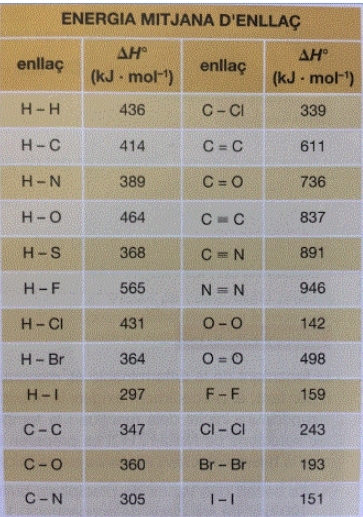
A partir de les dades de la taula, quin valor té l'entalpia estàndard de la reacció de cloració del metà?
Pista: Recordeu que heu de tenir present els enllaços que es trenquen i els que es formen en el procés.
Solució:
En la reacció de cloració del metà es trenquen 4 enllaços C-H i 4 enllaços Cl-Cl i es formen 4 enllaços C-Cl i 4 enllaços H-Cl.L’entalpia de la reacció serà:
ΔH° = Energia enllaços trencats – Energia d’enllaços formats =
= [4· EC-H + 4 · ECl-Cl ] ─ [4 · EC-Cl + 4 · EH-Cl] =
= [4 · 414 kJ/mol + 4 · 243 ] ─ [4 · 339 + 4 · 431 ] = -452 kJ
5. Considera les següents entalpies de combustió en condicions estàndard a 298K.
N2 (g) + O2 (g) → 2 NO (g) ΔH° = 180,7 kJ · mol-1
C (grafit) + O2 (g) → CO2 (g) ΔH° = -393,5 kJ · mol-1
C4H10 (g) + 13/2 O2 (g) → 4 CO2 (g) + 5 H2O (l) ΔH° = -2878 kJ · mol-1
Calculeu la quantitat de calor que produirà la combustió de:
a) 5 L de N2 mesurats a 1 atm i 298 K
b) 50 g de carboni (grafit)
c) 10 mols de C4H10
Solució:
a) n = (P·V)/(R·T) = (1 · 5 )/ 0,082 · 298) = 0,2 mols N2
0,2 mols · 180,7 kJ · mol-1 = 36,14 kJ
b) 50 g de C · 1 mol C/12 g C = 4,17 mols C
4,17 mols C · (-393,5 kJ · mol-1 )= - 1640,9 kJ
c) 10 mols de C4H10 · (-2878 kJ · mol-1) = - 28780 kJ