Exercici del vaixell a la deriva

a) L'equació general d'un MHS és y igual A cos parèntesi esquerre omega t més ϕ parèntesi dret. El desplaçament total és de 2 espai m, per tant l'amplitud serà la meitat: A igual 1 espai m. De forma semblant, si el temps d'anar del punt més baix al més alt és de 6.28 espai s espai igual fracció T entre 2, el període d'oscil·lació serà T igual 12.56 espai s i per tant omega igual fracció numerador 2 normal pi entre denominador T fi fracció igual 0.50 espai r a d dividit per s.

Tenint en comptes les condicions inicials: y parèntesi esquerre t igual 0 s parèntesi dret igual A igual 1 m, l'equació del MHS queda:

SOLUCIÓ y igual 1 per cos parèntesi esquerre 0.50 t parèntesi dret espai m espai o espai y igual 1 per sin obre parèntesis 0.50 t més fracció pi entre 2 tanca parèntesis espai m

b) Cal recordar que la velocitat i l'acceleració es dedueixen a partir de les expressions v igual fracció numerador d y entre denominador d t fi fracció i a igual fracció numerador d v entre denominador d t fi fracció, per tant:

v parèntesi esquerre t parèntesi dret igual menys 0.5 sin parèntesi esquerre 0.50 t parèntesi dret espai m dividit per s i a parèntesi esquerre t parèntesi dret igual menys 0.25 cos parèntesi esquerre 0.50 t parèntesi dret espai m dividit per s al quadrat.

Per al moment inicial, t igual 0 espai s:

SOLUCIÓ v parèntesi esquerre 0 parèntesi dret igual 0 espai m dividit per s i a parèntesi esquerre 0 parèntesi dret igual menys 0.25 espai m dividit per s al quadrat

Exercici de la corda de violoncel

a) Cal identificar els 3 ventres (V) i els 4 nodes (N):

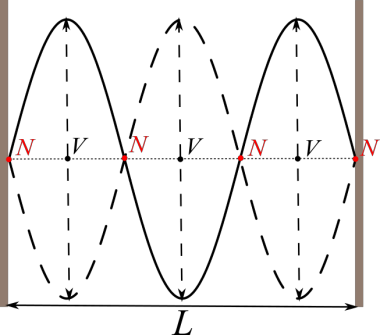
3r harmònic d'una ona a la corda d'un violoncel

La longitud d'ona lambda la podem deduir de L igual 1.5 lambda, on L igual 0.70 espai m. Una altra manera de trobar-ho és a partir de l'expressió els modes de vibració o harmònics d'una corda amb extrems fixos lambda subíndex h a r m ò n i c espai n fi subíndex igual fracció 2 entre n L en el cas particular de n igual 3.

La distància entre dos nodes consecutius ho trobem gràficament a partir de l'expressió 1 terç L igual 1 terç L per fracció 3 entre 2 lambda igual fracció lambda entre 2

SOLUCIÓ lambda igual 0.467 espai m, i la distància entre dos nodes consecutius és 0.233 espai m

b) El temps que triga, per a un ventre, la posició vertical a passar del seu valor màxim al mínim equival a mig període. Sabem que v igual lambda per f igual fracció lambda entre T fletxa dreta T igual fracció lambda entre v, per tant increment t igual fracció T entre 2 igual fracció numerador T lambda entre denominador v fi fracció

SOLUCIÓ increment normal t igual 7.58 per 10 elevat a menys 4 fi elevat normal s

Exercici de l'Estació Espacial Internacional

a) La velocitat orbital de l'estació la deduïm d'igualar l'expressió de la força gravitatòria amb l'expressió de la força centrípeta: F subíndex g r a v i t a t ò r i a fi subíndex igual F subíndex c e n t r í p e t a fi subíndex fletxa dreta G fracció numerador M subíndex T m subíndex e s t fi subíndex entre denominador r subíndex o r b i t a l fi subíndex superíndex 2 fi fracció igual fracció numerador m subíndex e v subíndex e s t fi subíndex superíndex 2 entre denominador r subíndex o r b i t a l fi subíndex fi fracció, per tant v subíndex e s t fi subíndex igual arrel quadrada de fracció numerador G M subíndex T entre denominador r subíndex o r b i t a l fi subíndex fi fracció fi arrel.

Cal tenir en compte que el radi de l'òrbita és el radi de la Terra més l'altura sobre la superfície terrestre a la qual es troba l'estació: r subíndex o r b i t a l fi subíndex igual R subíndex T e r r a fi subíndex més h.

El temps entre dues visualitzacions consecutives coincidirà amb el període: T igual fracció numerador 2 normal pi normal r subíndex orbital entre denominador v subíndex e s t fi subíndex fi fracció.

SOLUCIÓ v subíndex e s t fi subíndex igual 7.68 per 10 al cub espai m dividit per s i T igual 92.2 espai m i n

b) Ens demanen la velocitat addicional que cal donar al coet perquè afegida a la velocitat de l'estació, el coet assoleixi la velocitat d'escapament. Sabem que per a trobar la velocitat d'escapament cal aplicar la condició E subíndex m e c fi subíndex igual 0 espai J espai fletxa dreta E subíndex c i n fi subíndex igual menys E subíndex p o t fi subíndex, per tant 1 mig m subíndex c o e t fi subíndex v subíndex e s c fi subíndex superíndex 2 igual G fracció numerador M subíndex T m subíndex c o e t fi subíndex entre denominador r subíndex o r g fi subíndex fi fracció. Així doncs, fracció numerador G M subíndex T m entre denominador r al quadrat fi fracció igual fracció numerador m v al quadrat entre denominador r fi fracció fletxa dreta r igual fracció numerador G M subíndex T entre denominador v al quadrat fi fracció i v subíndex e s c fi subíndex igual arrel quadrada de fracció numerador G M subíndex T entre denominador r subíndex o r b i t a l fi subíndex fi fracció fi arrel. Obtenim que v subíndex e s c fi subíndex igual 1.09 per 10 elevat a 4 m dividit per s. La velocitat addicional que ens demanen serà increment v igual v subíndex e s c fi subíndex menys v subíndex e s t fi subíndex.

SOLUCIÓ increment v igual 3.18 per 10 al cub espai m dividit per s

Exercici de l'isòtop radioactiu fluor

a) El positró és l'antipartícula de l'electró, per tant C igual 0 espai i espai D igual 1. Cal utilitzar que en la desintegració s'ha de conservar el nombre atòmic Z i el nombre màssic A, per tant: 18 igual A més 0 i 9 igual B més 1.

El positró i l’electró s’anihilen donant lloc a 2 fotons idèntics que viatjaran en la mateixa direcció i sentit contrari. L’energia dels 2 fotons serà la que emmagatzemava la massa en repòs de les dues partícules que s’anihilen. Per tant: E igual 2 h ni igual 2 m c al quadrat fletxa dreta ni igual fracció numerador m c al quadrat entre denominador h fi fracció.

SOLUCIÓ A igual 18 coma espai B igual 8 coma espai C igual 0 espai i espai D igual 1, ni igual 1.24 per 10 elevat a 20 espai H z

b) Volem que N subíndex f i n a l fi subíndex igual 0.01 per N subíndex 0 i sabem que 0.01 N subíndex 0 igual N subíndex 0 e elevat a menys lambda t fi elevat.  Cal trobar lambda a partir del període de semidesintegració lambda igual fracció numerador ln espai 2 entre denominador T subíndex 1 dividit per 2 fi subíndex fi fracció igual fracció numerador ln espai 2 entre denominador 109.77 espai m i n fi fracció igual 6.3 per 10 al cub m i n elevat a menys 1 fi elevat. De 0.01 N subíndex 0 igual N subíndex 0 e elevat a menys lambda t fi elevat, obtenim que t igual fracció numerador menys ln espai 0.01 entre denominador lambda fi fracció, i per tant:

SOLUCIÓ t igual 729.30 espai m i n espai igual asimptòtic 12 h

Exercici de la superfície de coure

a) La freqüència llindar és la freqüència mínima que ha de tenir una radiació electromagnètica per a que els seus fotons puguin arrencar electrons d'un metall determinat per efecte fotoelèctric. De la gràfica, obtenim que:

SOLUCIÓ ni subíndex 0 igual 1.1 per 10 elevat a 15 H z

b) Cal tenir en compte que E subíndex c espai d e l s espai e l e c t r o n s espai e m e s o s fi subíndex igual E subíndex l l u m espai i n c i d e n t fi subíndex menys W subíndex 0. Sabem que E subíndex l l u m espai i n c i d e n t fi subíndex igual fracció numerador h c entre denominador lambda fi fracció i a més, que el treball d'extracció coincideix amb l'energia dels fotons amb freqüència llindar W subíndex 0 igual h ni subíndex 0. Per tant E subíndex c espai e l e c t r o n s espai e m e s o s fi subíndex igual fracció numerador h c entre denominador lambda fi fracció menys h ni subíndex 0 igual 7.282 per 10 elevat a menys 19 fi elevat J. Per trobar la velocitat d'aquests electrons emesos, apliquem la definició d'energia cinètica v igual arrel quadrada de fracció numerador 2 E subíndex c i n è t i c a espai d e l s espai e l e c t r o n s fi subíndex entre denominador m subíndex e fi fracció fi arrel, per tant:

SOLUCIÓ v igual 1.43 per 10 elevat a 6 espai m dividit per s

Darrera modificació: diumenge, 15 de desembre 2019, 15:00