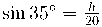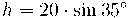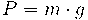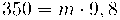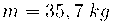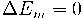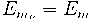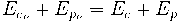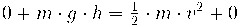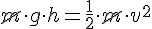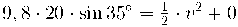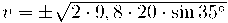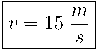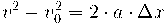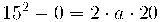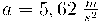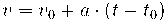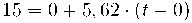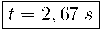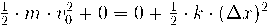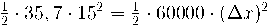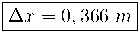Solució

1. Un objecte que pesa 350 N es troba inicialment en repòs al capdamunt d'una rampa de 20 m de llargada i una inclinació de 35^o amb l'horitzontal. L'objecte es deixa caure i al final de la rampa continua el seu moviment sobre un pla horitzontal sense fricció, on topa amb una molla de constant recuperadora k = 6·10⁴ N/m. [10 punts]

Dada: g= 9,8 m·s^-2

Calculeu:

a) L'energia cinètica i l'energia potencial gravitatòria de l'objecte a l'inici i al final de la rampa.

b) La velocitat que té l'objecte quan arriba al final de la rampa.

c) El temps que l'objecte triga a arribar al final de la rampa.

d) La deformació màxima que es produeix en la molla, si no s'ha perdut energia mecànica en la col·lisió.

e) Quina és la força elàstica que fa la molla sobre el cos en la situació d) ? Calculeu-la i representeu-la.

a) A l'inici de la rampa:

L'energia cinètica és 0 perquè el cos està en repòs. (0,2p)

L'energia potencial gravitatòria és (0,6p)

Càlcul de l'alçada h: Si la rampa té 20 m de llargada llavors l'alçada de l'objecte és:

$\sin 35^{\circ} = \frac{h}{20}$

$h = 20 \cdot \sin 35^{\circ}$ = 11,47 m  (0,2p)

Càlcul de la massa m: A partir del pes del cos calculem la seva massa:

$P = m \cdot g$

$350 = m \cdot 9,8$

$m = 35,7 \; kg$  (0,2p)

Al final de la rampa:

L'energia potencial gravitatoria és 0 perquè l'alçada és 0 (hem agafat l'origen d'altura al peu del pla inclinat). (0,2p)

L'energia cinètica és  

No tenim la velocitat, però sabem que l'energia mecànica es conserva perquè no hi ha fricció, així:    (0,6p)

b) L'energia del cos es conserva:

$\Delta E_m = 0$

$E_{m_{o}} = E_m$

$E_{c_{o}}+E_{p_{o}} = E_c + E_p$

$0 + m \cdot g \cdot h = \frac{1}{2} \cdot m \cdot v^2 + 0$

$\normalsize{\cancel m \cdot g \cdot h = \frac{1}{2} \cdot \cancel m \cdot v^2}$.  (1p)

si substituïm en l'equació anterior:

$9,8 \cdot 20 \cdot \sin 35^{\circ}= \frac{1}{2} \cdot v^2 + 0$

$v = \pm \sqrt{2 \cdot 9,8 \cdot 20 \cdot \sin 35^{\circ}}$

$\boxed{v=15 \; \frac{m}{s}}$ (1p)

c) Per a calcular el temps fem servir les equacions del MRUA:

$v^2 - v^{2}_{0} = 2 \cdot a \cdot \Delta x$

$15^2 - 0 = 2 \cdot a \cdot 20$

$a = 5,62 \;\frac{m}{s^2}$. (1p)

i el temps:

$v = v_0 + a \cdot (t - t_0)$

$15 = 0 + 5,62 \cdot (t - 0)$

$\boxed{t=2,67 \; s}$. (1p)

d) L'energia del cos es conserva i ara tenim energia potencial elàstica:

$\Delta E_m = 0$

$E_{m_{o}} = E_m$

$E_{c_{o}}+E_{p_{o}} = E_c + E_p$

$\frac{1}{2} \cdot m \cdot v^2_0 + 0 = 0 + \frac{1}{2} \cdot k \cdot (\Delta x)^2$. (1p)

si substituïm:

$\frac{1}{2} \cdot 35,7 \cdot 15^2 = \frac{1}{2} \cdot 60000 \cdot (\Delta x)^2$

$\boxed{\Delta x = 0,366 \; m}$. (1p)

e) La força elàstica és   (1p)

(1p)