Electrotècnia (Bloc 2) ~ gener 2020: Fórmules i conceptes

Sistemes electrònics digitals

Canvis de base

Qualsevol número en una base determinada es pot descompondre en potències d'aquesta base. Així el número 274,3 en base 10 (s'expressa 274,3₁₀)

274,3₁₀= 2·10² + 7·10¹ + 4·10⁰ + 3·10^-1

Si ho calculem

2·10² + 7·10¹ + 4·10⁰ + 3·10^-1 = 2·100 + 7·10 + 4· 1 + 3 ·0,3 = 274,3

Recordeu que n⁰ = 1

La generalització per a qualsevol base n ens permet canviar un número de qualsevol base a decimal

X_n = x_nⁿ + x_n-1^n-1 + .... +x₂² + x₁¹ + x₀⁰ + x_-1^-1 +... + x_-n^-n

Exemples:

143₈ = 1·8²+ 4·8¹+ 3·8⁰= 1·64 + 4·8 + 3·1= 64 + 32 + 3 = 99₁₀

10101₂ = 1·2⁴+0·2³+1·2²+0·2¹+1·2⁰= 1·16+0+1·4+0+1·1 = 16 + 4 + 1 = 21₁₀

Un problema afegit són les bases superiors a 10 i en particular el sistema hexadecimal (16). Solament disposem de 10 dígits per indicar els números (0, 1, 2, 3, ... , 8, 9) i en aquest cas en se'n precisen 16. Per solucionar aquest problema s'utilitzen lletres (A, B, C, D, E i F). Aquestes lletres tenen el seguen valor:

A = 10
B = 11
C = 12
D = 13
E = 14
F = 15

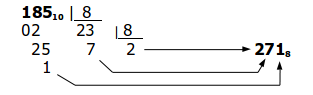
2DF₁₆ = 2·16² + D·16¹ + F·16⁰= 2·256 +13·16 +15· 1= 512 + 208 + 15 = 735₁₀

El sistema hexadecimal és el que utilitzen els programadors per treballar en codi màquina

Per fer l'operació inversa s'ha de dividir successivament per la base i recuperar el resultat final i els restes de cada divisió.

Divisió pel canvi de base

Podem verificar-ho.

271₈ = 2·8²+7·8¹+1·8⁰= 2·64 +7·8 +1·1 = 128 +56 +1 = 185₁₀

Lleis de Morgan

Aquestes lleis s’utilitzen per poder canviar el tipus de les funcions

La negació d’una suma lògica de dos elements és igual al producte de les negacions dels elements.

$envoltori superior a més b fi envoltori espai igual envoltori superior a per envoltori superior b$

La negació d’un producte lògic de dos elements és igual ala suma de les negacions dels elements.

$envoltori superior a per b fi envoltori espai igual espai envoltori superior a més envoltori superior b$

Exemple de transformació d'una funció expressada com a 3 portes OR a portes NAND .	$f igual parèntesi esquerre a més b amb barra a sobre més c parèntesi dret més parèntesi esquerre pila a més b més c amb barra a sobre amb barra a sobre parèntesi dret més parèntesi esquerre a amb barra a sobre més b més c parèntesi dret$
Neguem dos cops la 1a i la 3a. Al negar dos cops la la funció no varia	$f igual pila pila a més b amb barra a sobre més c amb barra a sobre amb barra a sobre més pila a més b més c amb barra a sobre amb barra a sobre més espai pila pila a amb barra a sobre més b més c amb barra a sobre amb barra a sobre$
Convertim els + en · trencan les negacions	$f igual espai pila a amb barra a sobre per pila b amb barra a sobre amb barra a sobre per c amb barra a sobre amb barra a sobre més a amb barra a sobre per b amb barra a sobre per pila c amb barra a sobre amb barra a sobre més pila pila a amb barra a sobre amb barra a sobre per b amb barra a sobre per c amb barra a sobre amb barra a sobre$
Trèiem les dobles negacions	$f igual espai pila a amb barra a sobre per b per c amb barra a sobre amb barra a sobre més a amb barra a sobre per b amb barra a sobre per c més pila a per b amb barra a sobre per c amb barra a sobre amb barra a sobre$
Neguem dos cops tota la funció.	$f igual espai pila pila pila a amb barra a sobre per b per c amb barra a sobre amb barra a sobre més a amb barra a sobre per b amb barra a sobre per c més pila a per b amb barra a sobre per c amb barra a sobre amb barra a sobre amb barra a sobre amb barra a sobre$
Convertim els + en · dividint la negació	$f igual espai pila pila pila a amb barra a sobre per b per c amb barra a sobre amb barra a sobre amb barra a sobre per pila a amb barra a sobre per b amb barra a sobre per c amb barra a sobre per pila pila a per b amb barra a sobre per c amb barra a sobre amb barra a sobre amb barra a sobre amb barra a sobre$
Trèiem les dobles negacions	$f igual pila espai parèntesi esquerre a amb barra a sobre per b per c amb barra a sobre parèntesi dret per parèntesi esquerre pila a amb barra a sobre per b amb barra a sobre per c amb barra a sobre parèntesi dret per parèntesi esquerre a per b amb barra a sobre per c amb barra a sobre parèntesi dret amb barra a sobre$

Vigileu. No és el mateix posar

ab amb barra a sobre igual pila normal a per normal b amb barra a sobre

que

normal a amb barra a sobre normal b amb barra a sobre igual normal a amb barra a sobre per normal b amb barra a sobre

Taules de Karnaugh
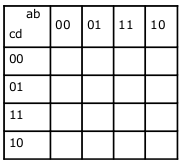
Per construir la taula hem de tenir en compte que només podem canvia un dels valors de les variables (00, 01, 11, 10) entre files o columnes.

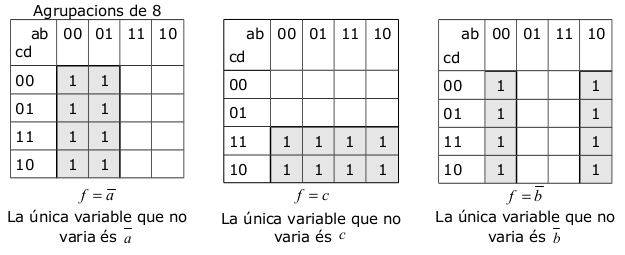
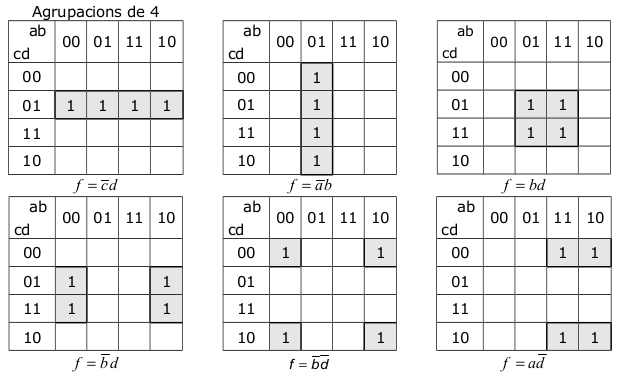
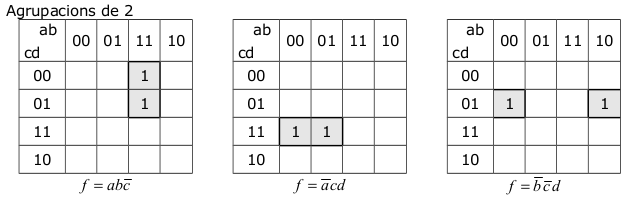
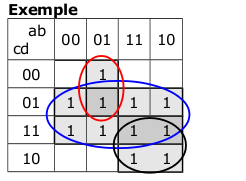
En les taules de Karnaugh de quatre variables és poden fer agrupacions de 8, 4 i 2. Fen tires o quadrats. Aquestes agrupacions és poden unir pels extrems de la taula. Per trobar la funció que li correspon a cada agrupació hem de descartar les variables que adopten els dos valors (0,1). Les que adopten un únic valor determinar, agafarem la funció sense negar, si té assignat un 1; i la funció negada si té assignat un 0. En les funcions on hi ha 4 variables, les agrupacions de 8 tindran sols una variable, les de 4, dos variables. Les de 2, tres variables i les que no tinguin agrupació tindran les 4 variables. És important fer el mínim de grups però que agafin el màxim de possibilitats.



$f igual espai d més a c més a amb barra a sobre b c amb barra a sobre$

Darrera modificació: dimecres, 18 d’abril 2018, 08:13

Propietat intel·lectual i drets d'autoria