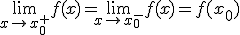Exercici 1 (7 punts)


f parèntesi esquerre x parèntesi dret igual obre claus taula atributs alineació columna left espai entre columnes 1.4ex fin atributos fila cel·la fracció numerador 2 entre denominador 3 x menys 2 fi fracció fi cel·la cel·la s i espai x menor o igual que menys 1 fi cel·la fila cel·la bold italic m x menys 1 fi cel·la cel·la s i espai menys 1 menor que x menor que 2 fi cel·la fila cel·la bold italic b x al quadrat més 2 x fi cel·la cel·la s i espai x major o igual que 2 fi cel·la fin tabla tanca


a) Quin és el domini de la funció? Cal estudiar el domini en cada una de les parts de la funció per separat i també els punts de transició d'una funció a l'altra.
b) Quin valor ha de tenir "b" i "m"per tal que la funció sigui contínua en x = -1 i en x = 2? Quins límits laterals s'han de calcular?
c) Digues si hi ha algun altre punt on s'ha d'estudiar la continuïtat, i cas que n'hi hagi de quin tipus de discontinuïtat es tracta

Resposta:

  • a) Domini de la funció f(x).

Cal estudiar cada una de les dues parts de la funció per separat i també els punts de transició d'una funció a l'altra.


Part I Punt de transició entre
 la part I i la II   
 Part II 
Punt de transició entre
 la part II i la III		 part  III
g parèntesi esquerre x parèntesi dret igual fracció numerador 2 entre denominador 3 x menys 2 fi fracció

Punt x = -1


p(x) = mx-1 x= 2
 h(x) =bx2+2x

g(x) és una funció racional.

I és discontínua en els punts on s'anul·la  el denominador. 

3x-2=0---> x=2/3


f parèntesi esquerre menys 1 parèntesi dret igual fracció numerador 2 entre denominador menys 3 menys 2 fi fracció igual fracció numerador 2 entre denominador menys 5 fi fracció


p(x) és una funció polinòmica i per tant contínua.      

No hi ha punts conflictius pel domini

punt x = 2

f(2)=b(2)2+2(2)=4b+4

h(x)  és una funció polinòmica

i per tant contínua.      

No hi ha punts conflictius pel domin
Dom g(x) =  Reals-{2/3} però x=2/3 no és d'aquesta part
  x = -1 és del domini
 Dom h(x) = Reals  x = 2 és del domini
Dom h(x) = Reals
Per tant  Dom f(x) = Reals


  • b) Quin valor ha de tenir "b" per tal que la funció sigui contínua en x = -1? 

Recordeu que una funció és contínua en un punt x0  :

\small {\lim} \limits_{x \to x_0^+}{f(x)}= \small {\lim} \limits_{x \to x_0^-}{f(x)}={f(x_0)}

Estudiarem el comportament de la funció en x = -1

  pila l i m amb x fletxa dreta parèntesi esquerre menys 1 parèntesi dret elevat a menys a sota f parèntesi esquerre x parèntesi dret igual pila l i m amb x fletxa dreta parèntesi esquerre menys 1 parèntesi dret elevat a menys a sota espai espai fracció numerador 2 entre denominador 3 x menys 2 fi fracció igual fracció numerador 2 entre denominador menys 3 menys 2 fi fracció espai igual fracció numerador 2 entre denominador menys 5 fi fracció  A l'esquerra de -1 li correspon la funció de la part I
  pila l i m amb x fletxa dreta parèntesi esquerre menys 1 parèntesi dret elevat a més a sota f parèntesi esquerre x parèntesi dret igual pila l i m amb x fletxa dreta parèntesi esquerre menys 1 parèntesi dret elevat a més a sota m x menys 1 igual m parèntesi esquerre menys 1 parèntesi dret menys 1 igual menys m menys 1  A la dreta de -1 li correspon la funció de la part II

f parèntesi esquerre menys 1 parèntesi dret igual fracció numerador 2 entre denominador menys 3 menys 2 fi fracció igual fracció numerador menys 2 entre denominador 5 fi fracció



Per tal que els tres valors coincideixen,  cal que:

   fracció numerador menys 2 entre denominador 5 fi fracció igual menys m menys 1 espai espai espai fletxa doble dreta envoltori caixa m igual fracció numerador menys 3 entre denominador 5 fi fracció fi envoltori

  • Repetim aquest mateix procediment per a x=2 . Estudiarem el comportament de la funció en x =2
límit quan x fletxa dreta 2 elevat a menys de m x menys 1 espai igual m parèntesi esquerre 2 parèntesi dret espai menys 1 espai igual espai 2 per parèntesi esquerre fracció numerador menys 3 entre denominador 5 fi fracció parèntesi dret menys 1 espai igual espai fracció numerador menys 6 entre denominador 5 fi fracció menys 1 igual fracció numerador menys 11 entre denominador 5 fi fracció límit quan x fletxa dreta 2 elevat a més de b x al quadrat més 2 x igual b per 2 al quadrat més 2 per 2 igual 4 b més 4 f parèntesi esquerre 2 parèntesi dret igual b per 2 al quadrat més 2 per 2 igual 4 b més 4


Per tal que els tres valors coincideixen,  cal que :   4 b més 4 igual fracció numerador menys 11 entre denominador 5 fi fracció espai espai espai fletxa doble dreta 4 b igual fracció numerador menys 11 entre denominador 5 fi fracció menys 4 negreta fletxa doble dreta 4 b igual fracció numerador menys 31 entre denominador 5 fi fracció fletxa doble dreta envoltori caixa b igual fracció numerador menys 31 entre denominador 20 fi fracció fi envoltori


 
  • c) Digues si hi ha algun altre punt on s'ha d'estudiar la continuïtat.

S'hauria  d'estudiar en x = 2/3 , però  aquest punt  correspon a la part II, on la funció és contínua en tots els seus punts. En tots cas, podríem comprovar-ho amb els límits

  •  Si en aquest punt presenta discontinuïtat, argumenta raonadament  de quin tipus és. 
Cal estudiar els límits laterals en x=2/3
límit quan x fletxa dreta obre parèntesis fracció 2 entre 3 tanca parèntesis elevat a menys de f parèntesi esquerre x parèntesi dret espai igual espai límit quan x fletxa dreta obre parèntesis fracció 2 entre 3 tanca parèntesis elevat a menys de m fracció 2 entre 3 menys 1 igual fracció numerador 2 m entre denominador 3 fi fracció menys 1 límit quan x fletxa dreta obre parèntesis fracció 2 entre 3 tanca parèntesis elevat a més de f parèntesi esquerre x parèntesi dret espai igual espai límit quan x fletxa dreta obre parèntesis fracció 2 entre 3 tanca parèntesis elevat a més de m fracció 2 entre 3 menys 1 igual fracció numerador 2 m entre denominador 3 fi fracció menys 1
f parèntesi esquerre fracció 2 entre 3 parèntesi dret espai igual espai igual fracció numerador 2 m entre denominador 3 fi fracció menys 1

    I aquest tres valors són coincidents, per tant la funció és contínua en x=2/3.


    Per tant la funció f(x) és contínua en tots els valor reals



     

         Exercici 2 (3 punts)

    Comproveu, utilitzant el teorema de Bolzano, que la funció   f parèntesi esquerre x parèntesi dret igual 2 x al cub menys x menys 10 té una arrel en l’interval [1,3], o el que és el mateix : l'equació 2 x al cub menys x menys 10 igual 0  té una solució en l'interval [1,3]
    Aproximeu el seu valor fins les dècimes.
    Argumenteu detalladament el procediment.



    Resposta:

    Apliquem el Teorema de Bolzano en l'interval  [1,3]

    a = 1

    b = 3

    La funció es continua en aquest interval, ja que és una funció polinòmica

    obre taula atributs alineació columna right fin atributs fila cel·la f espai c o n t í n u a espai e n espai parèntesi esquerre 1 coma 3 parèntesi dret fi cel·la fila cel·la f parèntesi esquerre 1 parèntesi dret igual 2 parèntesi esquerre 1 parèntesi dret al cub menys parèntesi esquerre 1 parèntesi dret menys 10 igual menys 9 menor que 0 fi cel·la fila cel·la f parèntesi esquerre 3 parèntesi dret igual 2 parèntesi esquerre 3 parèntesi dret al cub menys parèntesi esquerre 3 parèntesi dret menys 10 igual 41 major que 0 fi cel·la fi taula tanca claus fletxa doble dreta a p l i c a n t espai e l espai t e r o e m a espai d e espai B o l z a n o coma espai e x i s t e i x espai u n espai v a l o r espai " c " espai t a l espai q u e espai f parèntesi esquerre c parèntesi dret espai igual 0 espai espai o espai s i g u i espai h i a espai h a espai u n espai v a l o r espai e n t r e espai 1 espai i espai 3 espai q u e espai é s espai s o l u c i ó espai d e espai l apòstrof e q u a c i ó espai 2 x al cub menys x menys 10 igual 0


    Per tant el valor que busquem serà x=1,1   x= 1,2    x= 1,3 ...o   x= 2  x=2,1   x= 2,2    x= 2,3 ...o   x= 2,9

    Repetint el Teorema de Bolzano en altres intervals  podrem esbrinar quina dècima té la solució buscada


    Separarem l'interval (1  ,  3) en dos subintervals per exemple (1,  2) i (2  , 3) i repetirem el Teorema de Bolzano.

    Apliquem el Teorema de Bolzano en l'interval  (1,2)


    obre taula atributs alineació columna right fin atributs fila cel·la f espai c o n t í n u a espai e n espai parèntesi esquerre 1 coma 2 parèntesi dret fi cel·la fila cel·la f parèntesi esquerre 1 parèntesi dret igual 2 parèntesi esquerre 1 parèntesi dret al cub menys parèntesi esquerre 1 parèntesi dret menys 10 igual menys 9 menor que 0 fi cel·la fila cel·la f parèntesi esquerre 2 parèntesi dret igual 2 parèntesi esquerre 2 parèntesi dret al cub menys parèntesi esquerre 2 parèntesi dret menys 10 igual 4 major que 0 fi cel·la fi taula tanca claus fletxa doble dreta a p l i c a n t espai e l espai t e r o e m a espai d e espai B o l z a n o coma espai e x i s t e i x espai u n espai v a l o r espai " c " espai t a l espai q u e espai f parèntesi esquerre c parèntesi dret espai igual 0 espai espai o espai s i g u i espai h i espai h a espai u n espai v a l o r espai e n t r e espai 1 espai i espai 2 espai q u e espai é s espai s o l u c i ó espai d e espai l apòstrof e q u a c i ó espai 2 x al cub menys x menys 10 igual 0


    Per tant el valor que busquem serà x=1,1   x= 1,2    x= 1,3 ...o   x= 1,9

    Repetint el Teorema de Bolzano en altres intervals  podrem esbrinar quina dècima té la solució buscada


    Separarem l'interval (1  ,  2) en dos subintervals per exemple (1,  1,5) i (1,5  , 2) i repetirem el Teorema de Bolzano.

    Apliquem el Teorema de Bolzano en l'interval (1  ,  1,5)

     


    obre taula atributs alineació columna right fin atributs fila cel·la f espai c o n t í n u a espai e n espai parèntesi esquerre 1 coma espai espai 1 coma 5 parèntesi dret fi cel·la fila cel·la f parèntesi esquerre 1 parèntesi dret igual 2 parèntesi esquerre 1 parèntesi dret al cub menys parèntesi esquerre 1 parèntesi dret menys 10 igual menys 9 menor que 0 fi cel·la fila cel·la f parèntesi esquerre 1 coma 5 parèntesi dret igual 2 parèntesi esquerre 1 coma 5 parèntesi dret al cub menys parèntesi esquerre 1 coma 5 parèntesi dret menys 10 igual menys 4 coma 75 menor que 0 fi cel·la fi taula tanca claus fletxa doble dreta N o espai e s espai c u m p l e i x e n espai l e s espai c o n d i c i o n s espai d e l espai t e r o e m a espai d e espai B o l z a n o coma espai n o espai p o d e m espai d i r espai s i espai h i espai h a espai o espai n o espai u n a espai s o l u c i ó espai e n espai a q u e s t espai i n t e r v a l


    Per tant aplicarem el Teorema en l'interval (1,5  ,  2)


    obre taula atributs alineació columna right fin atributs fila cel·la f espai c o n t í n u a espai e n espai parèntesi esquerre 1 coma 5 espai espai coma espai 2 parèntesi dret fi cel·la fila cel·la f parèntesi esquerre 1 coma 5 parèntesi dret igual 2 parèntesi esquerre 1 coma 5 parèntesi dret al cub menys parèntesi esquerre 1 coma 5 parèntesi dret menys 10 igual menys 9 menor que 0 fi cel·la fila cel·la f parèntesi esquerre 2 parèntesi dret igual 2 parèntesi esquerre 2 parèntesi dret al cub menys parèntesi esquerre 2 parèntesi dret menys 10 igual 4 major que 0 fi cel·la fi taula tanca claus fletxa doble dreta a p l i c a n t espai e l espai t e r o e m a espai d e espai B o l z a n o coma espai e x i s t e i x espai u n espai v a l o r espai " c " espai t a l espai q u e espai f parèntesi esquerre c parèntesi dret espai igual 0 espai espai o espai s i g u i espai h i espai h a espai u n espai v a l o r espai e n t r e espai 1 coma 5 espai i espai 2 espai q u e espai é s espai s o l u c i ó espai d e espai l apòstrof e q u a c i ó espai 2 x al cub menys x menys 10 igual 0


    Es compleixen els requisits del Teorema i podem concloure que  hi ha un valor numèric entre 1,5 i 2  que és solució de l'equació. --> Existeix c del interval(1,5,  2)  tal que  f(c) = 0

    Per tant el valor que busquem serà x=1,5   x= 1,6    x= 1,7 ,.. o x= 1,9


    Repetint el Teorema de Bolzano en altres intervals  podrem esbrinar quina dècima té la solució buscada

    Separarem l'interval (1,5,   2) en dos subintervals per exemple (1,5,  1,7) i (1,7  , 2) i repetirem el Teorema de Bolzano.

    Apliquem el Teorema de Bolzano en l'interval (1,7  , 2)


    a = 1,7

    b = 2

    La funció es continua en aquest interval

    f(1,7) = 2·(1,7)3 -1,7-10  =-1,874< 0

    f(2)  >0

    La solució està entre 1,7 i 2, però observeu que ja estem molt a prop

    La solució està entre 1,7 i 2 però molt a prop de 1,7


    Provarem en l'interval (1,8  ,  2)

    a = 1,8

    b = 2

    La funció es continua en aquest interval

    f(1,8) = 2·(1,8)3 -1,8-10  = -0,136< 0

    f(2)  >0

    La solució està entre 1,8 i 2 , però observeu que ja estem molt a prop de l'1,8


    Repetim:

    Provarem en l'interval (1,8  ,  1,9)

    a = 1,8

    b = 1,9

    La funció es continua en aquest interval

    f(1,8) = 2·(1,8)3 -1,8-10  = -0,136< 0

    f(1,9) = 2·(1,9)3 -1,9-10  = 1,818> 0

    La solució està entre 1,8 i 1,9, per tant ja hem trobat el primer decimal de la solució.


    Es compleixen els requisits del Teorema i podem concloure que  hi ha un valor numèric entre 1,8 i 1,9 que és solució de l'equació. --> Existeix c de l'interval (1,8  , 1,9)  tal que  f(c) = 0

    Per tant és un valor entre 1,8 i 1,9 per tant la solució serà 1,8...

    La resposta és doncs : La solució d'aquesta equació és  x ≈ 1,8

     

    Darrera modificació: dilluns, 28 d’octubre 2019, 10:32