LL4_Aplicació derivades
Resum Lliurament 4
1. Creixement i extrems relatius
Creixement d'una funció en un punt
 |
 |
 |
|
f(x) és estrictament creixent en el punt A ( en x = 1) i |
g(x) és estrictament decreixent en el punt B ( en x = 2) i |
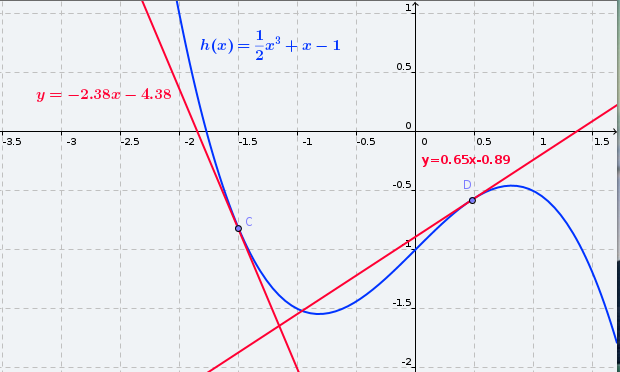
h(x) és estrictament decreixent en el punt C ( en x = -1.5) i h(x) és estrictament creixent en el punt D ( en x = 0.5) i |
Extrems relatius
Com trobar els intervals de monotonia
Per trobar els intervals de creixement i decreixement d'una funció f(x) seguim els següents passos :
1. Calcular f'(x) i resoldre l'equació f'(x) = 0 (possibles extrems).
2. Determinar els punts de discontinuïtat de la funció
3. Considerar els intervals limitats per les solucions de l'equació f'(x)=0 (trobats en el pas 1) i els punts de discontinuïtat (trobats en el pas 2).
4. Esbrinar el signe de f' en cadascun dels intervals anteriors calculant el signe de f' en un punt qualsevol d'aquest intervals. Amb el signe de f' sabrem si cada interval és de creixement o decreixement.
Com trobar els extrems relatius
Són punts on s'anul·la la derivada: f'(a)=0
(fixeu-vos que en un extrem la recta tangent sempre és horitzontal, o sigui té pendent 0)
Per saber si en x=a tal que f'(a)=0 hi ha un màxim o un mínim relatiu ho podem fer de dues maneres diferents:
a) substituïm en la derivada segona
si f''(a) > 0 => el punt (a,f(a)) és un mínim relatiu
si f''(a) < 0 => el punt (a,f(a)) és un màxim relatiu
b) (quan dibuixem funcions normalment ho farem d'aquesta manera)
si en l'interval a l'esquerra del punt la funció és creixent i en el de la dreta és decreixent => (a,f(a)) és màxim.
si en l'interval a l'esquerra del punt la funció és decreixent i en el de la dreta és creixent => (a,f(a)) és mínim.
Exemple molt senzill (sense discontinuïtats)
Estudiem el creixement, decreixement i extrems de la funció .
Procediment
-
- Calcular f ' (x). En aquest exemple f ' (x) = 2x
-
- Resoldre l'equació f ' (x)=0. Obtindrem els possibles extrems. En aquest cas seria 2x=0→ x=0. Aquí a=0
-
- Trobar els punts de discontinuïtat de la funció. La funció no té punts de discontinuïtat, ja que els polinomis són funcions contínues sempre.
-
- Ordenats de forma creixent els punts trobats, determinarem uns intervals. En el nostre cas només s'haurien format dos intervals: (-∞,0)(0,+∞)
-
- Estudiem els signe de la derivada en cada un dels intervals
En l'interval (-∞,0) podem triar per exemple x=-2. Calcularem f ' (-2). Que vol dir substituir x=-2 en f ' (x). Encara que el que importa només és el seu signe (+ o -).
f ' (-2) = 2·(-2) = -4 Per tant la funció f(x) és decreixent en tot l'interval al que pertany x = -2
En l'interval (0,+∞) podem triar per exemple x = 2. Calcularem f ' (2). Que vol dir substituir x=-2 en f ' (x). Encara que el que importa només és el seu signe (+ o -).
f ' (2) = 2·(2) = 4 Per tant la funció f(x) és creixent en tot l'interval al que pertany x=2
Resumint :
| Intervals | signe de f'(x) | f(x) és... |
| (-∞,0) | – | decreixent |
| (0,+∞) | + | creixent |
-
- Calculem l'ordenada dels punts estacionaris o extrems. Calculem la imatge de x=0, substituint x=0 en la funció f(x)→ f(0)=02=0
Com la funció a l'esquerra de x=0 és decreixent i a la dreta és creixent, necessàriament el punt x=0 és un mínim. La funció en el punt (0,0) té un mínim.