Equacions i funcions exponencials i logarítmiques.

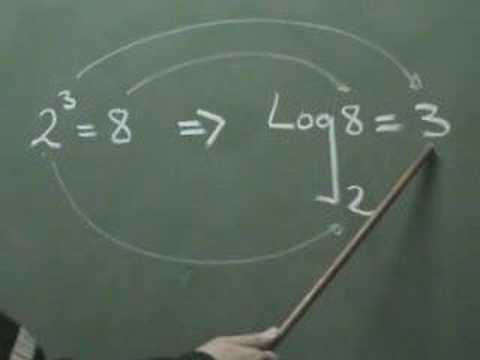
Funcions logarítmiques

Una funció logarítmica és aquella que té la variable independent aplicada a un logaritme.

En cas que la a=10 (logaritme decimal) no escrivim la base i per tant escrivim només  

En cas que la base sigui el nombre e, li diem logaritme neperià i la notació sol ser 

Característiques de la funció logaritme

• El seu domini són tots els reals estrictament positius: .
• El recorregut és tot R.
  
• Si la base a> 1 la funció és estrictament creixent.
• Si la base a compleix 0<a<1 la funció logaritme és estrictament decreixent.
• El punt de tall amb l'eix d'abscisses és (1,0)
• Té una asímptota vertical en x=0, és a dir quan la x tendeix a 0 (sempre per la part positiva) la funció s'acosta a o segons el valor de la a.

Càlcul de dominis

Quan calculem dominis de funcions logarítmiques s'ha d'imposar que la funció a qui se li aplica el logaritme sigui estrictament positiva.

Exemples

• . Aquesta funció està definida si x+3> 0 i per tant
  
  
• . Aquesta funció estarà definida si x²>0 per tant
  
  
  
• . Aquesta funció estarà definida si x²-1>0 per tant caldrà estudiar aquesta inequació.
  Resolem l'equació
  Aquests dos punts separen la recta real en tres intervals:
  Provarem un punts senzill interior a cada interval per saber quan és positiu:
  -Provem un punt interior a , per exemple el -2 :   (-2)² -1 = 4-1>0   interessa l'interval.
  -Provem un punt interior a , per exemple el 0 :   (0)² -1 = -1<0   no interessa l'interval.
  -Provem un punt interior a , per exemple el 2 :   (2)² -1 = 4-1>0   interessa l'interval.
  Conclusió: