Màquines i equilibri
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Tecnologia industrial I (Bloc 2) ~ gener 2020 |
| Llibre: | Màquines i equilibri |
| Imprès per: | Usuari convidat |
| Data: | dimecres, 26 de juny 2024, 13:47 |
1. Vectors
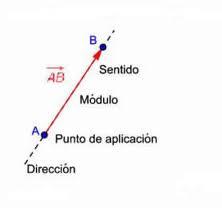
Recordeu que un vector és un element matemàtic que necessita, a més del valor propi (mòdul o intensitat), donar un punt d'aplicació, una direcció i un sentit. Es representa per una fletxa.
Suma i resta de vectors
Els vectors no es poden sumar directament sumant els seus valors, cal aplicar altres mètodes.
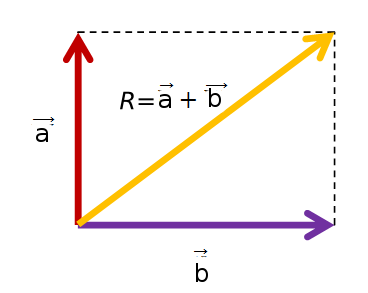
Per exemple, si tenim dos vectors a 90º com mostra la imatge on a = 3 m i b = 4 m, la resultant R serà R = 5 m que trobem aplicant el teorema de Pitàgores.
En cap cas podem fer la suma directa
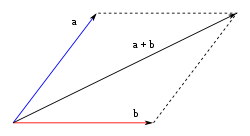
Per calcular la suma o resta de vectors en situacions diferents, s’ha de fer servir la trigonometria i els teoremes del sinus, cosinus, etc. els quals els podeu consultar en qualsevol llibre de física o matemàtiques.
El vector és la suma vectorial de
i
 =
=
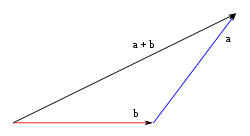
Producte escalar de dos vectors: Treball
Un producte escalar és una operació algebraica entre dos vectors que dóna un escalar (un número). El producte escalar de dos vectors és igual al producte de mòduls pel cosinus de l'angle que formen els dos vectors.
El treball (W), en Joules (J), és doncs un escalar que s'obté com a el producte de dos vectors, que són la força i l'espai. En la majoria dels casos la força i l'espai tenen la mateixa direcció, amb el cos 0º = 1, i per tant la fórmula queda així simplificada:
Producte vectorial de dos vectors: Moment d’una força respecte un punt
Un altre concepte que ens interessa de la Física és el producte vectorial.
El producte vectorial de dos vectors és un altre vector, perpendicular al pla format pels dos vectors que es multipliquen. El sentit del vector resultant és el que indica la llei del tirabuixó a l'anar del 1r sobre el 2n i el mòdul o intensitat és el producte dels mòduls pel sinus de l'angle que formen:
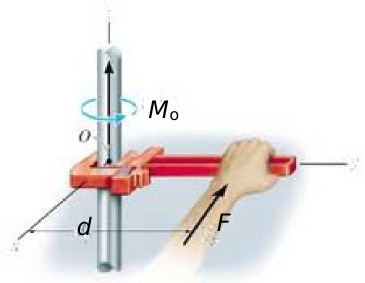
És important la fórmula del moment d'una força F respecte al punt O, on el vector serà la distància perpendicular d entre la força F i
el punt O, i així, com que el sin 90º = 1, la fórmula del moment per nosaltres serà:
El moment d'un vector respecte un punt és igual al valor de la força F en Newtons multiplicat per la distància perpendicular d en metres. El moment es mesura en N·m |
|
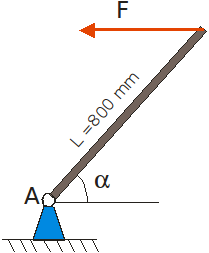
Exemple de càlcul de moment d’una força
Determineu el moment de la força F=1500 N sobre el punt A sabent que L=800 mm i α = 60º
|
|
Podem calcular primer la distancia perpendicular a F, i després el moment
o directament amb la fórmula general |
Parell de forces
Són dues forces paral·leles iguals i de sentit contrari. El càlcul del moment que provoquen és similar al cas anterior.
En aplicar un parell de forces a un cos, aquest gira, o es produeix una torsió. La magnitud de la rotació depèn del valor de la força i la distància entre elles. El parell de forces queda definit per:
|
El moment del parell de forces seria la suma del moment de cada una, ja que les dues fan girar el cos cap al mateix sentit: Si F1 = F2 = F i r1 = r2 = r → r + r = d llavors podem fer: |
2. Cinemàtica
Aquests conceptes bàsics corresponen als que podeu trobar en llibres de física.Velocitat lineal. És l'espai que recorre un cos linealment en un temps determinat.
En un moviment lineal uniforme de velocitat constant es verifica que:
La distancia d correspon al que anomenem en física espai e.
Les unitats que s'han d'utilitzar en S.I. són m/s, tot i que molts cops ens poden demanar múltiples com els km/h.
Velocitat angular. És l'angle que gira un cos en un determinat temps. L'angle s'ha de treballar en radians.
El moviment circular uniforme fa referència al moviment circular que experimenten els mecanismes com un pinyó, una politja o un engranatge, on el desplaçament angular per unitat de temps és constant.
|
La velocitat angular ω es mesura en rad/s (o també en s-1). Angle girat θ en rad i el temps t en s |
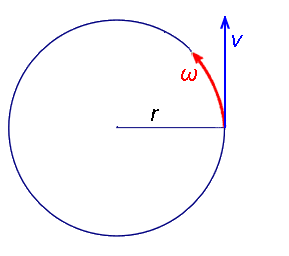
Relació entre la velocitat lineal i angular.
|
on r és el radi de gir en m |
 |
Relació entre els min⁻¹ i els rad/s. En alguns casos s'utilitza la freqüència angular n en comptes de la velocitat angular:
En aquest cas en S.I. es pot fer servir com unitat el min-1, ja que no és correcte posar revolucions per minut
La relació entre n (min-1) i ω (rad/s) és:
Potència de les màquines rotatives
En el cas de mecanismes que giren, és molt útil expressar la potència en funció de la velocitat de rotació, en comptes de fer-ho a través del treball dividit pel temps. Partint de la fórmula general, veiem que:
On P és la potència en watts , M és el moment de rotació en N·m i ω és la velocitat de rotació en rad/s.
I en el cas dels motors parlem de parell Γ en lloc de moment M
3. Equilibri
L'equilibri d'un cos es produeix quan aquest està en repòs o en moviment uniforme, però en el nostre cas tan sols considerarem quan el cos estarà en repòs.Es poden donar dues situacions:
1.- El cos està sotmès a forces concurrents
Direm que un cos sotmès a diferents forces concurrents en un punt està en equilibri quan la resultant de totes elles és zero.
Si les forces tenen la mateixa direcció es poden sumar directament, però quan les forces tenen direccions diferents s'ha de fer una suma de vectors utilitzant la trigonometria.
Exemple de càlcul d'equilibri d'un cos sotmès a forces concurrents d'igual direcció:
| La làmpada de la figura té una massa de m = 15 kg. Determineu la tensió de cable. P = m · g = 15 · 9,81 = 147,2 N
Per tant la tensió en el cable serà: T = P = 147,2 N |
 |
Exemple 1 de càlcul d'equilibri d'un cos sotmès a forces concurrents de diverses direccions:
| Determineu la tensió T1 i T2 que fa cada cable, si el cos té una massa de m =15 kg. La suma dels dos vectors de les forces T1 i T2 ha de donar una força igual a P. I com que el sistema és simètric: T1 = T2
P = m · g = 15 · 9,81 = 147,2 N P = T1 sin 45 + T2 sin 45 = 2T sin 45 |
Exemple 2 de càlcul d'equilibri d'un cos sotmès a forces concurrents de diverses direccions:
Una placa de metall rectangular de 2x1 metres, que pesa P = 616 N , està suspesa del sostre tal com es mostra a la figura. Determineu les forces que suporten els cables. La forma més fàcil de resoldre l'exercici és descomposar la força en les coordenades x, y i després plantejar l'equació d'equilibri per a cada direcció. |
|
|
Com que tot és simètric:
Per |
|
.
2.- El cos està sotmès a forces NO concurrents
En aquest cas per tal d'assegurar que el cos estigui en repòs no és suficient que la suma de forces sigui igual a zero , també s'ha de complir que la suma de moments que fan les forces respecte qualsevol punt del cos ha de ser també igual a zero
Exemple 1 de càlcul de moments en un cas d'equilibri d'un cos:
| En el sistema de la figura el pes de la barra és de P = 1000 N, la longitud de la barra és L =1 ,4 m i l’angle és α = 45º. Determineu la força FB que fa el tirant. |
Les forces que actuen sobre la barra són:
- El pes de la barra P
- La força del tirant FB
- La força que fa el recolzament sobre l'articulació en A RA.
Com que podem escollir el punt sobre el que calculem el moment, triem el que és més fàcil per nosaltres. En aquest cas triem el punt A perquè la força aplicada en aquest punt té dos components i s'anul·larà.
Cal recordar el signe triat segons el sentit de gir. Tan és quin trieu, però l'heu de mantenir per a tot el problema. Per exemple, si triem antihorari positiu i horari negatiu, seria:
- FB respecte A és positiu.
- P respecte A és negatiu.
- RA no dona moment perquè la seva distància fins a A és d = 0.
Exemple 2 de càlcul de moments en un cas d'equilibri d'un cos:
Considerem
el següent gronxador i trobem F1 i RO per tal que es mantingui en repòs:
Aquí
cal plantejar la suma de moments respecte el punt O igual a zero, és
a dir, les forces multiplicades per la distància perpendicular des
de O
.
A més el moment que fa cada força ha de portar signe positiu o
negatiu segons el sentit del gir que provocaria: el pes de 300 N fa girar el gronxador
en un sentit i la Força F1 en una altre. Agafem
ara positiu si gira en el sentit de les agulles del rellotge.
I ara per a calcular la força de reacció en el recolzament RO cal fer la suma de forces respecte l'eix de les Y igual a zero. (En l'eix X no hi ha forces)
També podríem haver calculat primer RO amb moments i després F1 amb forces, o totes dues forces amb moments.
4. Màquines simples
Una màquina és un sistema format per un conjunt de mecanismes que actuen conjuntament per a realitzar una tasca. Les maquines simples fan forces i transmeten parells.
Les màquines segueixen les lleis de la mecànica. Si es fa un estudi cinemàtic es poden calcular desplaçaments, velocitats i acceleracions. Si es fa un estudi dinàmic es poden calcular forces i moments.
Algunes de les màquines simples són:
La palanca
Una palanca és una màquina simple composta per una barra rígida que pot girar al voltant d'un punt de suport o fulcre. Es pot fer servir per a amplificar la força, o per a incrementar la distància recorreguda per un objecte en resposta a l'aplicació d'una força.
Si la palanca està en equilibri, es verifica que la suma de moments respecte el punt O val zero. El moment que genera la força F1 és igual i de sentit contrari al moment que genera la força F2:
|
palanca |
|
M = moment (N·m)
F = força (N)
d= distància de la força al fulcre (m) |
El torn
Un torn és una màquina simple que consisteix en un cilindre amb una corda al seu voltant, i una maneta. Girant la maneta també fem girar el cilindre i podem pujar masses. El torn també pot ser mogut per dues manetes, o també es pot accionar per un motor.
També es compleix que:
|
|
Per tant s’assembla molt a la palanca anterior.
|