Resum geometria mètrica

lloc:	Cursos IOC - Batxillerat
Curs:	Matemàtiques II (Bloc 1) ~ gener 2020
Llibre:	Resum geometria mètrica

Imprès per:	Usuari convidat
Data:	divendres, 21 de juny 2024, 22:31

Descripció

Resum geometria en l'espai

Taula de continguts

1. Posició relativa de dues rectes
2. Posició relativa de dos plans
3. Posició relativa entre recta i pla
4. Angles entre elements de l'espai
5. Distància entre elements de l'espai
6. Vídeos exemples
7. Exemple Simètric d'un punt

1. Posició relativa de dues rectes

Donades dues rectes de l'espai veiem com trobar la seva posició relativa depenent de:

- Si tenim les equacions implícites (ho vam veure ja en el lliurament 4):

r: $r dos punts espai obre claus taula fila cel·la A subíndex 1 x més B subíndex 1 y més C subíndex 1 z més D subíndex 1 igual 0 fi cel·la fila cel·la A subíndex 2 x més B subíndex 2 y més C subíndex 2 z més D subíndex 2 igual 0 fi cel·la fi taula tanca espai espai espai espai espai espai espai espai espai espai s dos punts espai obre claus taula fila cel·la A subíndex 3 x més B subíndex 3 y més C subíndex 3 z més D subíndex 3 igual 0 fi cel·la fila cel·la A subíndex 4 x més B subíndex 4 y més C subíndex 4 z més D subíndex 4 igual 0 fi cel·la fi taula tanca espai$

considerarem la matriu de coeficients i la matriu ampliada del sistema format per les equacions de les dues rectes:

$M igual obre parèntesis taula fila cel·la A subíndex 1 fi cel·la cel·la B subíndex 1 fi cel·la cel·la C subíndex 1 fi cel·la fila cel·la A subíndex 2 fi cel·la cel·la B subíndex 2 fi cel·la cel·la C subíndex 2 fi cel·la fila cel·la A subíndex 3 fi cel·la cel·la B subíndex 3 fi cel·la cel·la C subíndex 3 fi cel·la fila cel·la A subíndex 4 fi cel·la cel·la B subíndex 4 fi cel·la cel·la C subíndex 4 fi cel·la fi taula tanca parèntesis espai espai espai espai espai espai espai espai espai espai espai espai M apòstrof igual obre parèntesis taula fila cel·la A subíndex 1 fi cel·la cel·la B subíndex 1 fi cel·la cel·la C subíndex 1 espai espai menys D subíndex 1 fi cel·la fila cel·la A subíndex 2 fi cel·la cel·la B subíndex 2 fi cel·la cel·la C subíndex 2 subíndex 1 espai espai menys D subíndex 2 fi cel·la fila cel·la A subíndex 3 fi cel·la cel·la B subíndex 3 fi cel·la cel·la C subíndex 3 subíndex 1 espai espai menys D subíndex 3 fi cel·la fila cel·la A subíndex 4 fi cel·la cel·la B subíndex 4 fi cel·la cel·la C subíndex 4 subíndex 1 espai espai menys D subíndex 4 fi cel·la fi taula tanca parèntesis$

i mirarem els rangs de M i M'

Rectes coincidents rang M = rang M' = 2

Rectes paral·leles rang M = 2, rang M' = 3

Rectes secants rang M = rang M' = 3

Rectes que es creuen: rang M = 3, rang M' = 4

- Si sabem un punt i un vector director de cada recta.

$r e c t a espai r dos punts espai p u n t espai A coma espai v e c t o r espai d i r e c t o r espai u amb fletxa dreta a sobre espai espai r e c t a espai s dos punts espai p u n t espai B coma espai v e c t o r espai d i r e c t o r espai v amb fletxa dreta a sobre espai$

estudiarem els vectors $u amb fletxa dreta a sobre coma espai v amb fletxa dreta a sobre coma espai pila A B amb fletxa dreta a sobre$ i els punts A i B segons els cassos

Rectes coincidents:

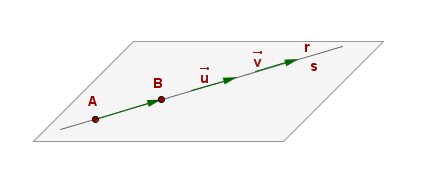
$negreta u amb negreta fletxa dreta a sobre negreta paral · lel negreta v amb negreta fletxa dreta a sobre negreta espai negreta espai negreta espai negreta espai bold italic i negreta espai negreta espai negreta espai negreta espai negreta espai bold italic A negreta pertany bold italic s espai espai espai espai parèntesi esquerre l l e g i m dos punts " u amb fletxa dreta a sobre espai é s espai p a r a l per l e l espai a espai v amb fletxa dreta a sobre espai i espai e l espai p u n t espai A espai é s espai d e espai l a espai r e c t a espai s parèntesi dret espai espai espai espai espai$

Rectes paral·leles:

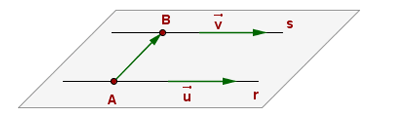
Rectes secants:

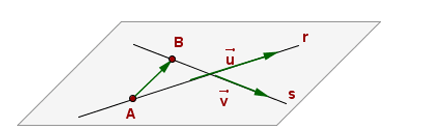
$negreta u amb negreta fletxa dreta a sobre no paral · lel negreta v amb negreta fletxa dreta a sobre negreta espai negreta espai negreta espai negreta espai bold italic i negreta espai negreta espai negreta espai negreta espai negreta espai bold italic d bold italic e bold italic t negreta espai negreta parèntesi esquerre negreta u amb negreta fletxa dreta a sobre negreta coma espai negreta v amb negreta fletxa dreta a sobre negreta coma negreta espai pila negreta A negreta B amb negreta fletxa dreta a sobre negreta parèntesi dret negreta igual negreta 0 espai espai$
(les dues rectes estan contingudes en un pla)

Rectes que es creuen:

$negreta u amb negreta fletxa dreta a sobre no paral · lel negreta v amb negreta fletxa dreta a sobre negreta espai negreta espai negreta espai negreta espai bold italic i negreta espai negreta espai negreta espai negreta espai negreta espai bold italic d bold italic e bold italic t negreta espai negreta parèntesi esquerre negreta u amb negreta fletxa dreta a sobre negreta coma espai negreta v amb negreta fletxa dreta a sobre negreta coma pila negreta A negreta B amb negreta fletxa dreta a sobre negreta parèntesi dret negreta no igual negreta 0 espai espai$

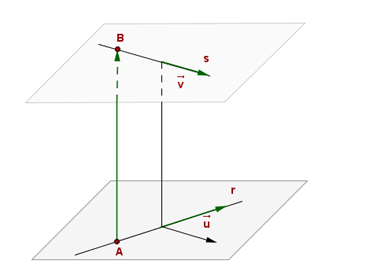
(les dues rectes no estan contingudes en un pla)

Exemple

En aquest vídeo veure explicació i un exemple:

2. Posició relativa de dos plans

Donats els plans

$majúscula pi subíndex 1 dos punts espai A x més B y més C z més D igual 0$

$majúscula pi subíndex 2 dos punts espai A apòstrof x més B apòstrof y més C apòstrof z més D apòstrof igual 0$

Coincidents

$fracció numerador A entre denominador A apòstrof fi fracció igual fracció numerador B entre denominador B apòstrof fi fracció igual fracció numerador C entre denominador C apòstrof fi fracció igual fracció numerador D entre denominador D apòstrof fi fracció$

(tots els coeficients són proporcionals)

De fet podem dir que són el mateix pla.

Paral·lels

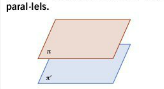
$fracció numerador A entre denominador A apòstrof fi fracció igual fracció numerador B entre denominador B apòstrof fi fracció igual fracció numerador C entre denominador C apòstrof fi fracció no igual fracció numerador D entre denominador D apòstrof fi fracció$

(els coeficients de les variables són proporcionals però no els termes independents)

No tenen cap punt comú.

Secants

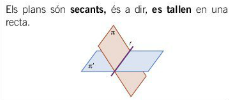
$fracció numerador A entre denominador A apòstrof fi fracció no igual igual fracció numerador B entre denominador B apòstrof fi fracció espai espai espai espai espai o espai espai espai fracció numerador A entre denominador A apòstrof fi fracció no igual fracció numerador C entre denominador C apòstrof fi fracció espai espai espai espai o espai espai espai espai espai fracció numerador B entre denominador B apòstrof fi fracció no igual fracció numerador C entre denominador C apòstrof fi fracció$

Els plans es tallen en una recta i l'equació implícita d'aquesta recta és

$obre claus majúscula pi subíndex 1 dos punts espai A x més B y més C z més D igual 0 majúscula pi subíndex 2 dos punts espai A apòstrof x més B apòstrof y més C apòstrof z més D apòstrof igual 0 tanca$

Exemple

En aquest vídeo podeu veure explicació i exemple.

3. Posició relativa entre recta i pla

Donats la recta i el pla d'equacions:

$r dos punts obre claus taula atributs alineació columna left fin atributs fila cel·la A subíndex 1 x més B subíndex 1 y més C subíndex 1 z més D subíndex 1 igual 0 fi cel·la fila cel·la A subíndex 1 x més B subíndex 1 y més C subíndex 1 z més D subíndex 1 igual 0 fi cel·la fi taula tanca espai espai espai espai espai espai espai majúscula pi dos punts espai A x més B y més C z més D igual 0$

per estudiar la seva posició relativa o podem veure de dues maneres:

a) Considerant les matrius

$M igual obre parèntesis taula fila cel·la A subíndex 1 fi cel·la cel·la B subíndex 1 fi cel·la cel·la C subíndex 1 fi cel·la fila cel·la A subíndex 2 fi cel·la cel·la B subíndex 2 fi cel·la cel·la C subíndex 2 fi cel·la fila A B C fi taula tanca parèntesis espai espai espai espai espai espai espai espai espai espai espai espai espai espai M apòstrof igual obre parèntesis taula fila cel·la A subíndex 1 fi cel·la cel·la B subíndex 1 fi cel·la cel·la C subíndex 1 espai espai menys D subíndex 1 fi cel·la fila cel·la A subíndex 2 fi cel·la cel·la B subíndex 2 fi cel·la cel·la C subíndex 2 espai espai menys D subíndex 2 fi cel·la fila A B cel·la C espai espai espai espai menys D fi cel·la fi taula tanca parèntesis$

Llavors:

	rang M	rang M'
Recta continguda en el pla	2	2
Recta i pla paral·lels	2	3
Recta i pla secants	3	3

Exemple:

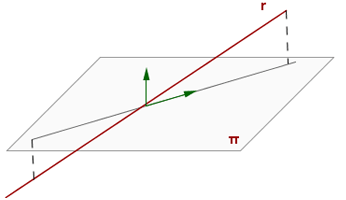
b) A partir del vector director i un punt de la recta y el vector normal del pla:

recta r: vector director $u amb fletxa dreta a sobre$ , punt A

pla Π: vector normal $n amb fletxa dreta a sobre$

Recta continguda en el pla:

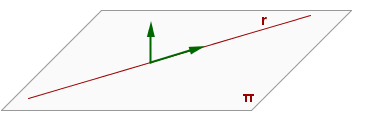
$negreta u amb negreta fletxa dreta a sobre negreta per negreta n amb negreta fletxa dreta a sobre negreta igual negreta 0 negreta espai negreta espai negreta espai negreta espai negreta espai bold italic i negreta espai negreta espai negreta espai negreta espai bold italic A negreta pertany negreta pi$

Recta i pla paral·lels:

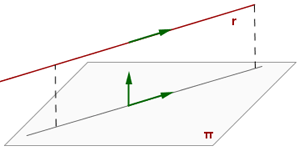
Recta i pla secants:

$negreta u amb negreta fletxa dreta a sobre negreta per negreta n amb negreta fletxa dreta a sobre negreta no igual negreta 0 negreta espai$

Exemple

Com a cas particular de recta i pla secants es pot considerar el cas de recta i pla perpendiculars. La recta i el pla seran perpendiculars quan el vector

u amb fletxa dreta a sobre

director de la recta r , i el vector i el vector normal

n amb fletxa dreta a sobre

pla Π siguin paral·lels. O sigui:

$v amb fletxa dreta a sobre igual k n amb fletxa dreta a sobre$

O expressat en components:

$u amb fletxa dreta a sobre igual parèntesi esquerre u subíndex 1 coma u subíndex 2 coma u subíndex 3 parèntesi dret n amb fletxa dreta a sobre igual parèntesi esquerre n subíndex 1 coma n subíndex 2 coma n subíndex 3 parèntesi dret$ $fracció u subíndex 1 entre n subíndex 1 igual fracció numerador estil mostrar u subíndex 2 fi estil entre denominador estil mostrar n subíndex 2 fi estil fi fracció igual fracció numerador estil mostrar u subíndex 3 fi estil entre denominador estil mostrar n subíndex 3 fi estil fi fracció$

Exemple

4. Angles entre elements de l'espai

Angle entre dues rectes

L'angle entre dues rectes és el menor angle que formen.

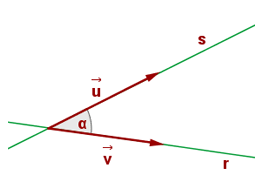
I és igual al'angle més petit format pels seus vectors director.

L'angle α l'obtenim a partir dels seus vectors directors.

$v amb fletxa dreta a sobre$ vector director r
$u amb fletxa dreta a sobre$ vector director s

$alfa igual a r c espai cos espai fracció numerador obre barra vertical u amb fletxa dreta a sobre per v amb fletxa dreta a sobre tanca barra vertical entre denominador obre barra vertical u amb fletxa dreta a sobre tanca barra vertical per obre barra vertical v amb fletxa dreta a sobre tanca barra vertical fi fracció$

És adir, si sabem les components dels vectors directors $v amb fletxa dreta a sobre parèntesi esquerre v subíndex 1 coma v subíndex 2 coma v subíndex 3 parèntesi dret$ , $u amb fletxa dreta a sobre parèntesi esquerre u subíndex 1 coma u subíndex 2 coma u subíndex 3 parèntesi dret$ ,
calculem el cosinus de l'angle que formen:

$cos espai alfa igual fracció numerador obre barra vertical u amb fletxa dreta a sobre per v amb fletxa dreta a sobre tanca barra vertical entre denominador obre barra vertical u amb fletxa dreta a sobre tanca barra vertical per obre barra vertical v amb fletxa dreta a sobre tanca barra vertical fi fracció igual fracció numerador obre barra vertical u subíndex 1 per v subíndex 1 més u subíndex 2 per v subíndex 2 més u subíndex 3 per v subíndex 3 tanca barra vertical entre denominador arrel quadrada de u subíndex 1 al quadrat més u subíndex 2 al quadrat més u subíndex 3 al quadrat fi arrel per arrel quadrada de v subíndex 1 al quadrat més v subíndex 2 al quadrat més v subíndex 3 al quadrat fi arrel fi fracció$

i un cop sabem el valor del cosinus de l'angle, amb la funció arcsinus, trobem l'angle.

Observació: agafem el mòdul del producte escalar per obtenir l'angle amb cosinus positiu, és a dir, el menor angle que formen.

Exemple

Trobeu l'angle que formen les rectes

$r dos punts espai espai fracció numerador x menys 2 entre denominador 2 fi fracció igual fracció numerador y més 1 entre denominador 1 fi fracció igual fracció z entre 1 espai espai espai espai espai espai espai espai espai espai espai s dos punts fracció numerador x més 1 entre denominador menys 1 fi fracció igual fracció y entre 2 igual fracció z entre 1$

Vectors directors:

$u parèntesi esquerre 2 coma 1 coma 1 parèntesi dret espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai v parèntesi esquerre menys 1 coma 2 coma 1 parèntesi dret$

$cos espai alfa igual fracció numerador obre barra vertical 2 per parèntesi esquerre menys 1 parèntesi dret més 1 per 2 més 1 per 1 tanca barra vertical entre denominador arrel quadrada de 2 al quadrat més 1 al quadrat més 1 al quadrat fi arrel per arrel quadrada de parèntesi esquerre menys 1 parèntesi dret al quadrat més 2 al quadrat més 1 al quadrat fi arrel fi fracció igual fracció numerador obre barra vertical 1 tanca barra vertical entre denominador arrel quadrada de 6 per arrel quadrada de 6 fi fracció igual fracció 1 entre 6$

Busqueu l'angle en la calculadora amb la funció inversa del cosinus, la funció arccosinus.

(fixeu-vos si teniu la calculadora en graus centígrads o radians)

$alfa igual a r c espai cos espai fracció 1 entre 6 igual negreta 80 negreta coma negreta 41 negreta º$

Angle entre dos plans

L'angle format per dos plans és l'angle menor determinat pels seus vectors normals.

$n amb fletxa dreta a sobre subíndex 1$ vector normal pla $majúscula pi subíndex 1$
$n amb fletxa dreta a sobre subíndex 2$ vector normal pla $majúscula pi subíndex 2$

$alfa igual a r c espai cos espai fracció numerador obre barra vertical pila n subíndex 1 amb fletxa dreta a sobre per pila n subíndex 2 amb fletxa dreta a sobre tanca barra vertical entre denominador obre barra vertical pila n subíndex 1 amb fletxa dreta a sobre tanca barra vertical per obre barra vertical pila n subíndex 2 amb fletxa dreta a sobre tanca barra vertical fi fracció$

Exemple

Troba l'angle format pels plans:

$normal pi subíndex 1 dos punts espai espai 2 normal x menys normal y més normal z menys 1 igual 0 espai espai espai espai espai espai espai espai espai normal pi subíndex 2 dos punts espai espai menys normal x menys normal z més 3 igual 0 espai espai espai espai espai espai$

Els vectors normals són:

$n subíndex 1 parèntesi esquerre 2 coma menys 1 coma 1 parèntesi dret n subíndex 2 parèntesi esquerre menys 1 coma 0 coma menys 1 parèntesi dret$

$cos espai alfa igual fracció numerador obre barra vertical 2 per parèntesi esquerre menys 1 parèntesi dret més parèntesi esquerre menys 1 parèntesi dret per 0 més 1 per parèntesi esquerre menys 1 parèntesi dret tanca barra vertical entre denominador arrel quadrada de 2 al quadrat més parèntesi esquerre menys 1 parèntesi dret al quadrat més 1 al quadrat fi arrel per arrel quadrada de parèntesi esquerre menys 1 parèntesi dret al quadrat més 0 al quadrat més parèntesi esquerre menys 1 parèntesi dret al quadrat fi arrel fi fracció igual fracció numerador obre barra vertical menys 3 tanca barra vertical entre denominador arrel quadrada de 6 per arrel quadrada de 2 fi fracció cos espai alfa igual fracció numerador 3 entre denominador arrel quadrada de 12 fi fracció igual fracció numerador 3 entre denominador 2 arrel quadrada de 3 fi fracció igual fracció numerador arrel quadrada de 3 entre denominador 4 fi fracció$

$alfa igual a r c espai cos espai fracció numerador arrel quadrada de 3 entre denominador 2 fi fracció igual negreta 30 negreta º$

Angle entre recta i pla

L'angle que formen una recta i un pla és l'angle format per la recta i la seva projecció ortogonal (perpendicular) sobre el pla.

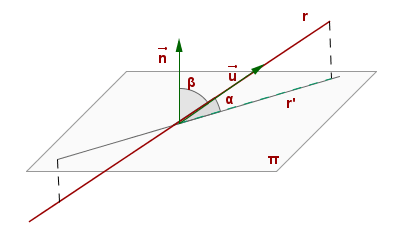
$v amb fletxa dreta a sobre$ vector director de la recta r

$n amb fletxa dreta a sobre$ vector normal del pla $majúscula pi$

$alfa igual a r c espai sin espai fracció numerador obre barra vertical v amb fletxa dreta a sobre per n amb fletxa dreta a sobre tanca barra vertical entre denominador obre barra vertical v amb fletxa dreta a sobre tanca barra vertical per obre barra vertical n amb fletxa dreta a sobre tanca barra vertical fi fracció$

5. Distància entre elements de l'espai

En els següents subapartats podeu veure com es calculen la distància entre dos elements (punts, rectes, plans) de l'espai.

Hem afegit exemples en els subapartats. I en aquest enllaç podeu trobar més exemples.

5.1. Distància entre dos punts

Distància entre dos punts A i B

És el mòdul del vector que va d'un punt a l'altre.

Punts $A igual parèntesi esquerre a subíndex 1 coma a subíndex 2 coma a subíndex 3 parèntesi dret$ i $B igual parèntesi esquerre b subíndex 1 coma b subíndex 2 coma b subíndex 3 parèntesi dret$

$bold italic d negreta parèntesi esquerre bold italic A negreta coma bold italic B negreta parèntesi dret negreta igual estil negreta barra vertical pila A B amb fletxa dreta a sobre barra vertical fi estil negreta igual arrel quadrada de negreta parèntesi esquerre negreta b subíndex negreta 1 negreta menys negreta a subíndex negreta 1 negreta parèntesi dret elevat a negreta 2 negreta més negreta parèntesi esquerre negreta b subíndex negreta 2 negreta menys negreta a subíndex negreta 2 negreta parèntesi dret elevat a negreta 2 negreta més negreta parèntesi esquerre negreta b subíndex negreta 3 negreta menys negreta a subíndex negreta 3 negreta parèntesi dret elevat a negreta 2 fi arrel$

Exemple
Calculeu la distància del punt A(3,2,-1) al punt B(5,4,0)

pila mida 14px A mida 14px B amb mida 14px fletxa dreta a sobre mida 14px igual mida 14px parèntesi esquerre mida 14px 2 mida 14px coma mida 14px 2 mida 14px coma mida 14px 1 mida 14px parèntesi dret mida 14px espai mida 14px espai mida 14px espai mida 14px espai mida 14px espai mida 14px espai mida 14px espai mida 14px d mida 14px parèntesi esquerre mida 14px A mida 14px coma mida 14px b mida 14px parèntesi dret mida 14px igual mida 14px espai estil mida 14px barra vertical pila A B amb fletxa dreta a sobre barra vertical fi estil mida 14px igual arrel quadrada de mida 14px 2 elevat a mida 14px 2 mida 14px més mida 14px 2 elevat a mida 14px 2 mida 14px més mida 14px 1 elevat a mida 14px 2 fi arrel mida 14px igual arrel quadrada de mida 14px 4 mida 14px més mida 14px 4 mida 14px més mida 14px 1 fi arrel mida 14px igual arrel quadrada de mida 14px 9 mida 14px igual mida 14px 3

5.2. Distància de punt a pla

Distància d'un punt P a un pla

És la mínima distància des del punt P a un punt qualsevol del pla. Aquesta mínima distància s'obté amb el punt projecció perpendicular del punt P sobre el pla.

$P igual parèntesi esquerre p subíndex 1 coma p subíndex 2 coma p subíndex 3 parèntesi dret normal pi dos punts espai Ax més By més Cz més normal D igual 0$

$envoltori caixa espai normal d parèntesi esquerre normal P coma normal pi parèntesi dret igual fracció numerador barra vertical Ap subíndex 1 més Bp subíndex 2 més Cp subíndex 3 més normal D barra vertical entre denominador arrel quadrada de normal A al quadrat més normal B al quadrat més normal C al quadrat fi arrel fi fracció espai fi envoltori$

Observacions:
- el valor absolut del numerador és per tal que sempre ens doni un nombre positiu.
- Si el punt és del pla, lògicament ens donarà que la distància es 0

Exemple 1
Trobeu la distància del punt P(-1,3,2) al pla

normal pi dos punts espai 2 normal x menys normal y més 3 normal z menys 5 igual 0

P parèntesi esquerre negreta menys negreta 1 coma negreta 3 coma negreta 2 parèntesi dret

En el numerador substituïm les coordenades del punt en l'equació del pla.

d parèntesi esquerre P coma normal pi parèntesi dret igual fracció numerador obre barra vertical 2 per parèntesi esquerre negreta menys negreta 1 parèntesi dret menys negreta 3 més 3 per negreta 2 menys 5 tanca barra vertical entre denominador arrel quadrada de 2 al quadrat més parèntesi esquerre menys 1 parèntesi dret al quadrat més 3 al quadrat fi arrel fi fracció igual fracció numerador obre barra vertical menys 4 tanca barra vertical entre denominador arrel quadrada de 14 fi fracció igual fracció numerador 4 entre denominador arrel quadrada de 14 fi fracció quasi igual a 1 coma 07

Exemple 2

5.3. Distància de punt a recta

Distància d'un punt P a una recta r

Necessitem saber el vector director i un punt qualsevol de la recta.

Siguin

Q punt qualsevol de la recta
$v amb fletxa dreta a sobre$ vector director de la recta

Llavors:

$envoltori caixa negreta espai negreta d negreta parèntesi esquerre negreta P negreta coma negreta r negreta parèntesi dret negreta igual fracció numerador estil negreta barra vertical QP amb fletxa dreta a sobre multiplicació en creu v amb fletxa dreta a sobre barra vertical fi estil entre denominador estil negreta barra vertical v amb fletxa dreta a sobre barra vertical fi estil fi fracció negreta espai fi envoltori$

Exemple
Trobeu la distància del punt $P parèntesi esquerre 2 coma 1 menys 1 parèntesi dret$ a la recta r: $fracció numerador x menys 5 entre denominador 2 fi fracció igual fracció y entre 3 igual fracció numerador z més 2 entre denominador menys 1 fi fracció$

Amb l'equació que ens donen de la recta tenim:
Punt qualsevol de la recta: Q(5,0,-2)
Vector director (2,3,-1)

$estil mida 14px pila Q P amb fletxa dreta a sobre igual parèntesi esquerre 5 coma 0 coma menys 2 parèntesi dret menys parèntesi esquerre 2 coma 1 coma menys 1 parèntesi dret igual parèntesi esquerre 3 coma menys 1 coma menys 1 parèntesi dret fi estil$

$estil mida 14px pila Q P amb fletxa dreta a sobre multiplicació en creu v amb fletxa dreta a sobre igual obre barra vertical taula fila i j k fila 3 cel·la menys 1 fi cel·la cel·la menys 1 fi cel·la fila 2 3 cel·la menys 1 fi cel·la fi taula tanca barra vertical igual obre barra vertical taula fila cel·la menys 1 fi cel·la cel·la menys 1 fi cel·la fila 3 cel·la menys 1 fi cel·la fi taula tanca barra vertical i menys obre barra vertical taula fila 3 cel·la menys 1 fi cel·la fila 2 cel·la menys 1 fi cel·la fi taula tanca barra vertical j més obre barra vertical taula fila 3 cel·la menys 1 fi cel·la fila 2 3 fi taula tanca barra vertical k igual 4 i més j més 11 k espai espai Per espai tant dos punts espai espai espai espai espai espai espai espai espai espai pila Q P amb fletxa dreta a sobre multiplicació en creu v amb fletxa dreta a sobre igual parèntesi esquerre 4 coma 1 coma 11 parèntesi dret fi estil$

$d parèntesi esquerre P coma r parèntesi dret igual fracció numerador obre barra vertical QP amb fletxa dreta a sobre multiplicació en creu normal v amb fletxa dreta a sobre tanca barra vertical entre denominador obre barra vertical normal v amb fletxa dreta a sobre tanca barra vertical fi fracció igual fracció numerador arrel quadrada de 4 al quadrat més 1 al quadrat més 11 al quadrat fi arrel entre denominador arrel quadrada de 2 al quadrat més 3 al quadrat més parèntesi esquerre menys 1 parèntesi dret al quadrat fi arrel fi fracció igual fracció numerador arrel quadrada de 138 entre denominador arrel quadrada de 14 fi fracció quasi igual a 0 coma 84$

Observació:

Ho podem fer sense aplicar la fórmula seguint el següents passos:

- Trobem el pla perpendicular a la recta que passa pel punt P: $2 x més 3 y menys z menys 8 igual 0$

- Trobem la intersecció del pla anterior amb la recta: $obre parèntesis fracció 31 entre 7 coma menys fracció 6 entre 7 coma menys fracció 12 entre 7 tanca parèntesis$

- $estil mida 14px d parèntesi esquerre P coma r parèntesi dret igual d obre parèntesis parèntesi esquerre 2 coma 1 coma menys 1 parèntesi dret coma obre parèntesis fracció 31 entre 7 coma menys fracció 6 entre 7 coma menys fracció 12 entre 7 tanca parèntesis tanca parèntesis igual arrel quadrada de obre parèntesis fracció 31 entre 7 menys 2 tanca parèntesis al quadrat més obre parèntesis menys fracció 6 entre 7 menys 1 tanca parèntesis al quadrat més obre parèntesis menys fracció 12 entre 7 més 1 tanca parèntesis al quadrat fi arrel igual espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai igual arrel quadrada de obre parèntesis fracció 17 entre 7 tanca parèntesis al quadrat més obre parèntesis menys fracció 13 entre 7 tanca parèntesis al quadrat més obre parèntesis menys fracció 5 entre 7 tanca parèntesis al quadrat fi arrel quasi igual a 0 coma 84 fi estil$

5.4. Distància entre dues rectes

Distància entre dues rectes r i s

a) Rectes coincidents o secants.

$bold italic d negreta parèntesi esquerre bold italic r negreta coma bold italic s negreta parèntesi dret negreta igual negreta 0$

b) Rectes paral·leles

Es calcula la distància d'un punt qualsevol d'una recta a l'altra recta.

Sigui P punt qualsevol de la recta r

$bold italic d negreta parèntesi esquerre bold italic r negreta coma bold italic s negreta parèntesi dret negreta igual bold italic d negreta parèntesi esquerre bold italic P negreta coma bold italic s negreta parèntesi dret$

c) Rectes que es creuen

La distància entre dues rectes que es creuen es defineix com la mínima distància d'un punt d'una de les rectes a un punt de l'altre.

P punt de r, $normal u amb fletxa dreta a sobre$ vector director de s
Q punt de s, $v amb fletxa dreta a sobre$ vector director de s

$bold italic d negreta parèntesi esquerre bold italic r negreta coma bold italic s negreta parèntesi dret negreta igual fracció numerador obre barra vertical obre claudàtors pila negreta P negreta Q amb negreta fletxa dreta a sobre negreta coma negreta u amb negreta fletxa dreta a sobre negreta coma negreta v amb negreta fletxa dreta a sobre tanca claudàtors tanca barra vertical entre denominador obre barra vertical negreta u amb negreta fletxa dreta a sobre negreta multiplicació en creu negreta v amb negreta fletxa dreta a sobre tanca barra vertical fi fracció$

Recordeu (estudiat en el lliurament 3) que $estil mida 14px obre claudàtors normal u amb fletxa dreta a sobre coma normal v amb fletxa dreta a sobre coma normal w amb fletxa dreta a sobre tanca claudàtors fi estil$ indica el producte mixt i es calcula:

$estil mida 14px obre claudàtors u amb fletxa dreta a sobre coma espai v amb fletxa dreta a sobre coma espai w amb fletxa dreta a sobre tanca claudàtors igual u amb fletxa dreta a sobre per parèntesi esquerre v amb fletxa dreta a sobre espai x espai w amb fletxa dreta a sobre espai parèntesi dret igual obre barra vertical taula fila cel·la u subíndex 1 fi cel·la cel·la u subíndex 2 fi cel·la cel·la u subíndex 3 fi cel·la fila cel·la v subíndex 1 fi cel·la cel·la v subíndex 2 fi cel·la cel·la v subíndex 3 fi cel·la fila cel·la w subíndex 1 fi cel·la cel·la w subíndex 2 fi cel·la cel·la w subíndex 3 fi cel·la fi taula tanca barra vertical fi estil$

Exemple
https://www.geogebra.org/m/d9EQyj3M

5.5. Distància entre dos plans

Distància entre dos plans $negreta pi negreta espai negreta i negreta espai negreta espai negreta pi negreta apòstrof$

a) Plans coincidents o secants.

$bold italic d negreta parèntesi esquerre negreta pi negreta coma negreta pi negreta apòstrof negreta parèntesi dret negreta igual negreta 0$

b) Plans paral·lels.

En aquest cas la distància entre els dos plans la podem trobar de dues maneres:

1. La distància entre els dos plans serà la distància d'un punt qualsevol d'un dels plans a l'altre pla.

Per tant, trobem un punt P qualsevol del pla $normal pi$ , i llavors:

$bold italic d negreta parèntesi esquerre negreta pi negreta coma negreta pi negreta apòstrof negreta parèntesi dret negreta igual bold italic d negreta parèntesi esquerre bold italic P negreta coma negreta pi negreta apòstrof negreta parèntesi dret$

2. Donats dos plans paral·lels:

$normal pi dos punts espai espai espai Ax més By més Cz més normal D igual 0 normal pi apòstrof dos punts espai Ax més By més Cz més normal D apòstrof igual 0$

Llavors:

$bold italic d negreta parèntesi esquerre negreta pi negreta coma negreta pi negreta apòstrof negreta parèntesi dret negreta igual fracció numerador obre barra vertical negreta D negreta menys negreta D negreta apòstrof tanca barra vertical entre denominador arrel quadrada de negreta A elevat a negreta 2 negreta més negreta B elevat a negreta 2 negreta més negreta C elevat a negreta 2 fi arrel fi fracció$

Atenció: fixeu-vos que per poder aplicar aquesta fórmula, els dos plans han d’estar donats amb
els mateixos coeficients de x, y, z. Això sempre serà possible si els plans són paral·lels.

Per exemple, els plans

$normal pi dos punts espai espai espai normal x menys 2 normal y més normal z més 2 igual 0 normal pi apòstrof dos punts espai 3 normal x menys 6 normal y més 3 normal z més 5 igual 0$

són paral·lels, d'acord?

llavors si l'equació del pla $normal pi apòstrof$ la dividim tota entre 3, ens queda:

$normal pi apòstrof dos punts espai espai x menys 2 y més z més fracció 5 entre 3 igual 0$

Ara $normal pi apòstrof$ sí el tenim amb els mateixos coeficients de x, y, z que $normal pi$ i ja podrem aplicar la fórmula:

$normal pi dos punts espai espai espai normal x menys 2 normal y més normal z més 2 igual 0 normal pi apòstrof dos punts espai espai normal x menys 2 normal y més normal z més fracció 5 entre 3 igual 0$

$d parèntesi esquerre normal pi coma normal pi apòstrof parèntesi dret igual fracció numerador obre barra vertical 2 menys estil mostrar fracció 5 entre 3 fi estil tanca barra vertical entre denominador arrel quadrada de 1 al quadrat més parèntesi esquerre menys 2 parèntesi dret al quadrat més 1 al quadrat fi arrel fi fracció igual fracció numerador estil mostrar 1 terç fi estil entre denominador 6 fi fracció igual fracció 1 entre 16$

5.6. Distància entre recta i pla

Distància entre recta r i pla Π

a) Si la recta està continguda en el pla o la recta i el pla són secants

$bold italic d negreta parèntesi esquerre bold italic r negreta coma negreta pi negreta parèntesi dret negreta igual negreta 0$

b) Si la recta i el pla són paral·lels

En aquest cas l distància entre la recta i el pla és la distància d'un punt qualsevol de la recta al pla.

P punt qualsevol de la recta r

$bold italic d negreta parèntesi esquerre bold italic r negreta coma negreta pi negreta parèntesi dret negreta igual bold italic d negreta parèntesi esquerre bold italic P negreta coma negreta pi negreta parèntesi dret$

6. Vídeos exemples

Tots aquests vídeos (en castellà) són de Youtube però em sembla que us poden ajudar ja què considero que estan molt bé explicats pas a pas.

Recta perpendicular a un pla, que passa per un punt

Distància d'un punt a un pla (amb fómula)

Distància d'un punt a una recta (sense fórmula)

Distància d'un punt a una recta (amb fòrmula)

7. Exemple Simètric d'un punt

En aquest enllaç:

Simètric d'un punt

podeu veure un exemple de trobar el simètric d'un punt

b) Respecte d'una recta.

c) Respecte d'un pla.