Resum Geometria afí
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques II (Bloc 1) ~ gener 2020 |
| Llibre: | Resum Geometria afí |
| Imprès per: | Usuari convidat |
| Data: | dimarts, 18 de juny 2024, 15:52 |
Descripció
Dubtes freqüents: Geometria
Taula de continguts
- 1. Rectes en l'espai
- 2. Plans en l'espai
- 3. Punt i vector director d'una recta donada amb equació implícita.
- 4. Coordenades d'un punt i d'un vector
- 5. Vector normal del pla
- 6. Feix de plans.
- 7. Components d'un vector
- 8. Intersecció recta i pla
- 9. Gràfics en 3D Geogebra
- 10. Posició relativa de dues rectes donades en forma implícita
1. Rectes en l'espai
Donats
vector director
Punt
Equació vectorial
Equació paramètrica
Equació contínua
Equació implícita
Exemple
Equacions de la recta que passa pel punt i té vector director
Equació vectorial:
Equació paramètrica
Equació contínua:
Equació implícita
l'obtenim de l'anterior:
Observació: si tenim l'equació implícita d'una recta, per saber punt i vector director veieu:
Punt i vector director d'una recta donada amb equació implícita.2. Plans en l'espai
Plans en l'espai
Un pla de l'espai queda determinat per un punt P i dos vectors linealment independents que anomenarem vectors directors o orientadors del pla.
Tres punts A, B, C no alinats també determinen un pla ja que a partir d'aquests 3 punts també podem obtenir els dos vectors directors, per exemple,
Equacions d'un pla
Donats
vectors orientadors
Punt
Equació vectorial
Equació paramètrica
Equació general o implícita
La podem obtenir fent:
Exemple 1
Equacions del pla que passa pel punt i té vectors directors
Equació vectorial:
Equació paramètrica:
Equació implícita
Observació: també ho podem fer calculant el vector normal del pla: Vector normal del pla
Exemple 2
Trobeu l'equació general del pla que passa pels punts
Trobem vectors directors:
Equació general:
Podem simplificar:
Com trobar punts d'un pla?
per trobar un punt d'un pla es donen valors qualssevol a dues variables i es calcula l'altra variable. Exemple:
Volem un punt qualsevol del pla 2x-y+3z+5=0
Agafem, per exemple
3. Punt i vector director d'una recta donada amb equació implícita.
Veiem diferents maneres de trobar un punt i un vector director d'una recta donada en equació implícita
</p>
<p><br>Una de les maneres més senzilles de trobar un vector director de la recta és fent el producte vectorial dels vectors normals dels plans que determinen la recta. O sigui:</p>
<p>vector director:
</p>
<p>i per trobar un punt, donem un valor qualsevol a una variable i, resolem el sistema per trobar les altres dues variables. </p>
<p></p>
<p><span style="text-decoration: underline;"><strong>Exemple.</strong></span></p>
<p>recta </p>
<p>
</p>
<p><strong></strong></p>
<p><strong>vector director:</strong>
</p>
<p>Fem aquest producte vectorial:</p>
<p>
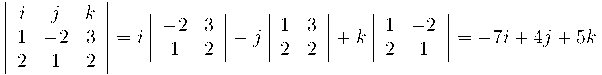
Per tant, un vector director de la recta és (-7,4,5)
Fixeu-vos que tant podem agafar el vector (-7,4,5) com el (7,-4,-5)
Punt.
Donem un valor qualsevol a una de les variables.
Agafem, per exemple z=0
Per trobar les coordenades x, y hem de resoldre el sistema:
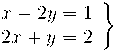
la solució d'aquest sistema és x=1, y=0
Per tan, un punt de la recta és (1,0,0)
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Podeu veure en aquest vídeos dos mètodes més per trobar un punt i un vector director de la recta:
a) Trobant dos punts qualsevol A i B de la recta. El vector director serà el vector
b) Trobant l'equació paramètrica de la recta. Llavors les components del vector director seran els coeficients del paràmetre en l'equació:
4. Coordenades d'un punt i d'un vector
(Ho farem en 2 dimensions per simplificar els gràfics però la idea és la mateixa en 3 dimensions)
Aclariment referent a les coordenades d'un punt:
Les coordenades d'un punt són les que són. Que vull dir amb això?
Mireu la representació del punt A i la del punt B

Evidentment A i B són punts diferents.
Un vector queda caracteritzat pel seu mòdul, la seva direcció i el seu senti.
El vector
no són el mateix vector, de fet
El mòdul (la longitud del vector) del vector
Però el vector
Llavors quan el que ens interessa és la direcció podem agafar tant el vector
És per això que si volem el vector director d'una recta, el vector normal d'un pla,.... com que el que ens importa és la direcció podem agafar indistintament un o altre (encara que no siguin iguals).
5. Vector normal del pla
Donat el pla
el vector normal o vector característic del pla és .
En el llibre d'Edebé, en el tema 6 (lliurament 4) no l'utilitza. Ho utilitza i ho explica en el tema 7 (lliurament 5). Però és molt pràctic utilitzar-ho i us pot anar molt bé en molts casos per trobar fàcilment l'equació general del pla.
Aquest vector és molt important. És un vector que és perpendicular al pla. O sigui, que és perpendicular als dos vectors directors del pla.
Per tant, si sabem els vectors directors del pla, fent el producte vectorial dels plans obtenim aquest vector normal i, per tant, obtenim els coeficients del pla.
Exemple 1
Trobeu l'equació general del pla que té vector normal i passa pel punt P(5,-1,0).
L'equació general del pla serà de la forma :
I si el punt (5,-1,0) ha de ser del pla, s'ha de complir:
L'equació general del pla és:
Exemple 2
Trobeu l'equació general del pla que té vectors directors , i
i passa pel punt P(-1,1,-1).
El seu vector normal serà
Fem aquest producte vectorial:
Per tant, l'equació general del pla serà de la forma:
I trobem D per tal que passi pel punt (-1,1,-1):
L'equació general del pla és:
Observació: aquesta equació del pla també la podem trobar fent el determinant:
Exemple 3
Trobeu l'equació general del pla perpendicular a la recta i que passa pel punt P(-1,0,3).
Si recta i pla són perpendiculars, el vectors director de la recta (2,3,-1) serà un vector perpendicular al pla, per tant serà el seu vector normal.
Pla amb vector normal (2,3,-1):
calculem D perquè passi pel punt P(-1,0,3):
Equació general del pla:
6. Feix de plans.
Definició
Donada una recta r, anomenem feix de plans al conjunt de plans que passen per aquesta recta.
Equació del feix de plans que passen per una recta.
Si tenim la recta:
La tenim expressada com a intersecció de dos plans:
L'equació del feix de plans que contenen a la recta és:
donant valors qualssevol als paràmetres λ i μ obtenint plans que passen per la recta.
Per fer-ho més senzill podem considerar un únic paràmetre i llavors expressem així el feix de plans:
o bé
En general és indiferent a quin pla li posem el paràmetre però tingueu en compte la observació que faig al final d'aquest apartat.
Exercici de feix de plans.
Els exercicis on podem considerar el feix de plans són els exercicis que ens demanen l'equació d'un pla que passa per una recta i alguna altra condició.
Encara que aquests exercicis, en general, també es podrien fer d'altres maneres.
Exemple.
Donades les rectes
Trobar el pla que conté r i és paral·lel a la recta s.
Si teniu l procediment de a resolució que dóna el llibre és:
1) Considerar el feix de plans (secants) que contenen a la recta r.
D'aquests plans volem el que sigui paral·lel a la recta r
Condició de paral·lelisme de recta i pla:
Una recta de vector director és paral·lela a un pla de vector normal
si
és perpendicular a
, o sigui si el producte escalar d'aquest dos vectors és 0
Ho podem expressar així:
 Es veu la condició en aquest petit dibuix (al vector director de la recta li ha posat
Es veu la condició en aquest petit dibuix (al vector director de la recta li ha posat )
En geometria en l'espai és molt important que feu un petit dibuix com aquest. O que agafeu un llapis (recta) i un full (pla) i veieu la situació.
Si ho fem amb aquesta condició.
vector normal del pla:
Vector director de la recta s:
El pla del faig, amb és
podem multiplicar tota l'equació per 5:
-----------------------------------------------------------------------------------------------------------------------------------------------------
Quan expressem el feix de plans importa quin pla multipliquem per λ?
En la majoria de cassos no importa. En quins cassos importa?. Veiem un exemple.
Exemple:
Vull el pla que conté la recta i passa pel punt P(2,0,-1)
La solució seria justament el pla (ja que aquest pla passa pel punt P i, evidentment, conté a la recta)
En aquest cas, no podríem agafar el faig amb en el primer pla.
Veiem que passa si agafem:
O sigui,
ho podem posar a qualsevol dels dos plans excepte en el cas que justament el pla solució sigui un dels que defineixen la recta. En aquest cas
s'ha de posar a l'altre pla.
És per això que moltes vegades s'usen dos paràmetres diferents, un per a cada cada pla, encara que en la majoria de cassos amb un és suficient (i queda més senzill).
Bé, és una mica subtil però espero que ho entengueu.
7. Components d'un vector
Podem multiplicar per un nombre les components d'un vector ?
Depèn. Depèn de que ens interessi del vector.
Per exemle, si hem obtingut com a vector director d'una recta el vector , per tal de no treballar amb fraccions, en comptes del vector
podem agafar el vector
, no són iguals però tenen la mateixa direcció i tant el
com el 4
són vectors directors de la recta i es pot agafar qualsevol dels dos com a vector director d'una recta.
Però si, per exemple, ens interessa el mòdul del vector, evidentment no serà el mateix agafar el vector que el 4
. Si tenen el mateix mòdul el vector
i el vector -
Atenció:
Les coordenades d'un punt mai es poden multiplicar o dividir per un nombre. Un punt té les coordenades que té i si les modifiquem obtenim altre punt. El punt (2,2,4) és un punt diferent al (1,1,2)
8. Intersecció recta i pla
Si tinc una recta i un pla que es tallen en un punt, com trobo aquest punt d'intersecció?
Hem de trobar la intersecció però aquesta intrrssecció la podem trobar de diferents maneres depenent de quin tipus d'equació tenim de la recta. Aconsello:
a) Si tenim l'equació implícita de la recta
recta pla
Podem resoldre el sistema d'equacions format per les equacions de la recta i el pla
Resolem aquest sistema (per exemple, per Gauss), la solució és (1,1,1)
b) Si sabem un punt i el vector director de la recta (o sigui, equació contínua o paramètrica)
recta r. punt (-1,0,4), vector director (2,1,-3)
O sigui, tindríem l'equació paramètrica de la recta:
Pla:
En aquest cas, per fer la intersecció substituim directament la x, y, z de la recta en l'equació del pla. O sigui:
I substituint aquest valor de λ en l'equació paramètrica obtenim el punt:
9. Gràfics en 3D Geogebra
Les representacions d'elements a l'espai (3 dimensions) no és senzill.
Per exemple, representar un punt ja és treballós (en 2 dimensions és molt senzill). Per situar el punt (2,3,-4) en un sistema de coordenades hem de fer:
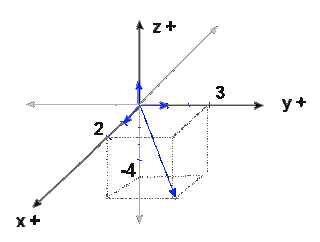
Especialment per fer gràfics és molt útil el programa Geogebra, ho podeu descarregar o podeu utilitzar la versió on line:
Quan entreu veureu diverses opcions:
El geogebra clàssic aquí es pot treballar la geometria al pla
Graficador GeoGebra 3D aquí podreu representar elements de l'espai. A l'esquerra, en "Entrada", podeu l'equació del que vulgueu representar: un punt (1,-2,3), un pla x+y-z=0. Per exemple per dibuixar la recta. podeu definir dos punts i triar l'opció recta per dos punts. O un punt i una recta,... és qüestió que, si teniu curiositat, jugueu una mica amb totes les opcions.
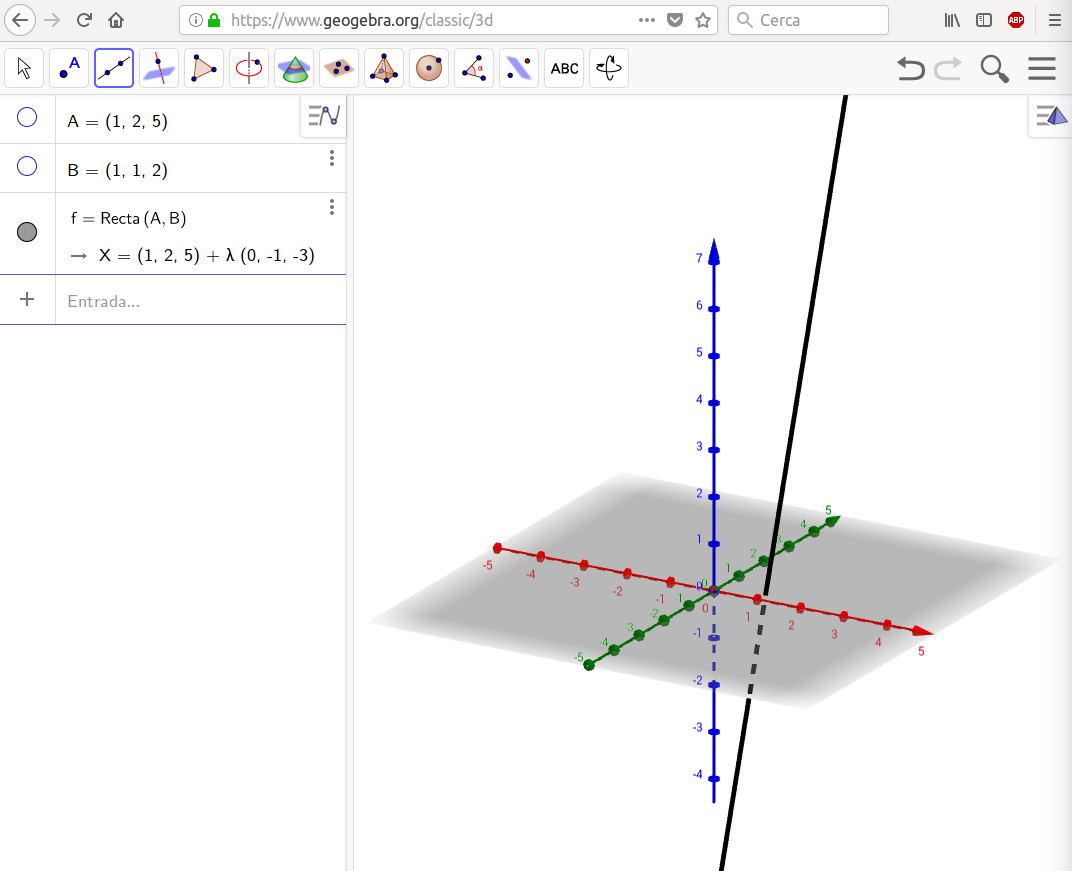
De totes maneres us comento aquesta eina per si teniu curiositat però, en general, els dibuixos no els farem acuradament. El que ens interessa en general és l'esquema. Vull dir que si, per exemple, tenim dos punts i volem un pla perpendicular a la recta que passa per ells,.... simplement farem un dibuix del tipus

10. Posició relativa de dues rectes donades en forma implícita
Donades dues rectes de l'espai veiem com trobar la seva posició relativa depenent de:
- Si tenim les equacions implícites:
r:
considerarem la matriu M de coeficients i la matriu ampliada M' del sistema format per les equacions de les dues rectes:
i mirarem els rangs de M i M'
Rectes coincidents rang M = rang M' = 2
Rectes paral·leles rang M = 2, rang M' = 3
Rectes secants rang M = rang M' = 3
Rectes que es creuen rang M = 3, rang M' = 4