Vectors de l'espai
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques II (Bloc 1) ~ gener 2020 |
| Llibre: | Vectors de l'espai |
| Imprès per: | Invitado |
| Data: | divendres, 24 de maig 2024, 08:52 |
Descripció
Dubtes freqüents vectors
1. Punts i vectors en l'espai
Punts i vectors en
Un sistema de coordenades ortogonal en l'espai es construeix traçant 3 eixos perpendiculars entre sí.
Un vector és un segment orientat que va d'un punt A (origen) a un punt B (extrem)
 Elements d'un vector:
Elements d'un vector:
Direcció: direcció de la recta que el conté.
Sentit: el que va de l'origen a l'extrem.
Mòdul: longitud del segment AB, es representa per
Components d'un vector
Si les coordenades dels punts A i B són:
Les components del vector són les coordenades de l'extrem menys les de l'origen.
Exemple
Si les coordenades dels punts són:
Les components del vector són:
És la longitud del segment que el defineix.
El mòdul de un vector es representa per
i es calcula:
Punt mitjà d'un segment
Les coordenades del punt mitjà, M, d'un segment d'extrems els punts A(a1,a2,a3) i B(b1,b2,b3) són:
Observació:
El punt mitjà és el punt que divideix el segment en dues parts iguals.
En https://matematicasies.com/Divide-segmento-en-3-partes podeu veure un exemple de com trobar els punts que divideixen els segment en 3 parts iguals. I de manera anàloga es faria per trobar els punts que divideixen el segment en n parts iguals.
2. Operacions amb vectors
Suma de vectors
Multiplicació d'un vector per un nombre real
un nombre real
Aquest vector té:
Mòdul: el mòdul de multiplicat pel valor absolut de k
Direcció: la mateixa que el vector
Sentit: el mateix que el de si k és positiu
el oposat de si k és negatiu
Producte escalar de dos vectors
El producte escalar de dos nombres és un nombre (un escalar) que s'obté:
on α és l'angle format pels vectors
Si sabem les components dels vectors:
Una de les utilitats del producte escalar és per saber si dos vectors són perpendiculars:
dos vectors són perpendiculars si el seu producte escalar és 0
Producte vectorial de dos vectors
El producte vectorial de dos vectors és un vector que té:
- Mòdul: on α és l'angle menor format pels vectors
- Direcció: perpendicular al vector i al vector
- Sentit: el d'avanç d'un llevataps que gira de a
recorrent l'angle menor.
Si sabem les components dels vectors, llavors podem obtenir les components del producte vectorial:
Observació:
El producte escalar s'escriu amb punt i el resultat és un nombre.
El producte vectorial s'escriu amb creu i el resultat és un vector.
Aplicacions del producte vectorial
- Obtenció d'un vector perpendicular a dos donats.
Això ho utilitzarem molt en els següents temes de geometria. Per obtenir un vector perpendicular a dos vectors donats, farem el producte vectorial d'ells:
- Àrea del paral·lelogram i del triangle.
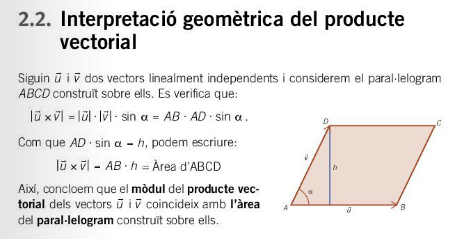
Per tant, l'àrea del paral·lelogram és:
I l'àrea del triangle serà la meitat de l'àrea del paral·lelogram:
Producte mixt
El producte mixt de tres vectors és un nombre que es calcula:
Interpretació geomètrica del producte mixt:
El valor absolut del producte mixt de tres vectors és el volum del paral·lelepípede construït sobre ells.
3. Càlcul d'àrees i volums
Us copiem aquests exemples extrets de la pàgina web http://calculo.cc/temas/temas_geometria_analitica/geo_metrica/teoria/area_vol.html
4. Punts alineats i paral·lelisme
Com sé si 3 punts formen un triangle o estan alineats?
"3 punts A, B, C no formen un triangle si estan alineats".
Si dibuixem 3 punts A, B i C que estan alineats (o sigui, sobre una mateixa recta), i dibuixem els vectors podem veure que aquests vectors tenen la mateixa direcció (o sigui, són paral·lels).
Recordem la condició de paral·lelisme (en qualsevol dimensió):
La condició de paral·lelisme de dos vectors és que les components dels vectors siguin proporcionals, o sigui, que els vectors són linealment dependents:
Això ho llegim així : dos vectors són paral·lels si i només si les seves components són proporcionals, o si i només si són linealment dependents
o bé: dos vectors són paral·lels és equivalent a dir que les seves components són proporcionals i equivalent a dir que són linealment dependents.
(Aquesta condició és la mateixa per components de vectors del pla, amb 2 components).
El que volem és que els 3 vectors siguin paral·lels, o sigui dependents dos a dos, per tant el rang dels 3 vectors ha de ser 1.
5. Angle entre vectors
Angle que formen dos vectors
Per trobar l'angle que formen dos vectors
donats per les seves components, utilitzem el producte escalar:
i tenint el valor de del cosinus, amb la funció arc cosinus trobem l'angle
Observacions:
- El valor del cosinus es deixa amb el signe que surti d'aplicar la fórmula.
- La funció encara que molts de vosaltres escriviu cos-1, és més correcte escriure arccos
- El arccos ho calculeu amb la calculadora (heu de fixar-vos si la teniu en radians o en graus
Angle que formen dues rectes de vectors directors
És diferent quan calculem l'angle entre dues rectes (ho farem en els següents lliuraments), perquè llavors si és pren l'angle més petit que formen, i llavors en la fórmula agafem el valor absolut del producte escalar.
Vectors perpendiculars
La condició perquè dos vectors siguin perpendiculars és que el seu producte escalar sigui 0.
(ho llegim així: dos vectors són perpendiculars és equivalent a dir que el seu producte escalar és 0)
Aquesta condició surt directament de la fórmula per trobar l'angle que formen 2 vector, ja que si són perpendiculars, l'angle que formen és de 90º, i cos 90l' = 0 però la destaco aquí per la importància de la condició.
6. Dependència-independència vectors
Referent a dependència- independència de vectors, base de l'espai,...... tingueu clares aquestes proposicions:
-------------------------------------------------------------------------------------------------------------------------
Siguin 3 vectors v1, v2, v3 de l'espai
v1, v2, v3 linealment independents rang {v1, v2, v3} = 3
det(v1,v2,v3)
0
O, el que és mateix:
v1, v2, v3 linealment dependents rang {v1, v2, v3} < 3
det(v1,v2,v3)=0
-----------------------------------------------------------------------------------------------------
Siguin v1, v2, v3 vectors de l'espai
v1, v2, v3 formen base de R3 v1, v2, v3 linealment independents
rang {v1, v2, v3} = 3
det(v1,v2,v3)
0
O, el que és mateix:
v1, v2, v3 no formen base de R3 v1, v2, v3 linealment dependents
rang {v1, v2, v3} < 3
det(v1,v2,v3)=0
-----------------------------------------------------------------------------------------------------
4 vectors de l'espai (de R3) sempre són linealment dependents
Més general:
En l'espai, un conjunt de més de 3 vectors sempre és linealment dependents.
-----------------------------------------------------------------------------------------------------
Qualsevol base de R3 està formada per 3 vectors linealment independents
7. Repàs vectors 2 i 3 dimensions
Els vectors de (2 dimensions, geometria en el pla) s'han estudiat en cursos anteriors.
Aquí teniu uns enllaços en cas que vulgueu repassar alguna cosa dels vectors:
Vectors de :
Vectors de