LL4_Geometria
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques aplicades a les C. socials II (Bloc 1) ~ gener 2020 |
| Llibre: | LL4_Geometria |
| Imprès per: | Usuari convidat |
| Data: | dilluns, 13 de maig 2024, 11:44 |
Descripció
Geometria
Taula de continguts
- 1. Geometria en el pla
- 2. Punts i vectors
- 3. Qüestions bàsiques
- 4. Equacions de la recta
- 5. Gràfica d'una recta
- 6. Exemples trobar equació recta
- 7. Equació de la recta que passa per dos punts
- 8. Posició relativa de dues rectes
- 9. Exemples. Posició relativa
- 10. Rectes paral·leles, exemple.
- 11. Recta perpendicular
- 12. llibre: equació de la recta
1. Geometria en el pla
En aquest lliurament estudiarem els vectors i les rectes del pla.
El que més ens interessa és saber treballar amb les rectes: dibuixar-les, trobar punts, trobar la seva equació, saber trobar el pendent,.....
Ho aplicarem en l'últim lliurament.
Si trobeu a faltar algun material no dubteu en preguntar en el fòrum de dubtes de l'aula i ho afegirem o indicarem on ho podeu trobar.
2. Punts i vectors
Punts en un sistema de coordenades cartesianes.

Vectors
Un vector és un segment orientat que va d'un punt A (origen) a un punt B (extrem
 Elements d'un vector:
Elements d'un vector:
Direcció: direcció de la recta que el conté.
Sentit: el que va de l'origen a l'extrem.
Mòdul: longitud del segment AB, es representa per
Components d'un vector
Si les coordenades dels punts A i B són:
Les components del vector són les coordenades de l'extrem menys les de l'origen.
Exemple
 Si les coordenades dels punts són:
Si les coordenades dels punts són:
Les components del vector són:
3. Qüestions bàsiques
Qüestió 1
Com sabem si un punt és d'una recta ax+by+c=0 ? Exemple: Donada la recta El punt (5,1) és de la recta r? substituïm els valors x=5, y=1 en l'equació de la recta: 3·5-2·1+1= 0 ? 15-2+1=0 ? NO El punt (3,5) és de la recta r? substituïm els valors x=3, y=5 en l'equació de la recta: 3·3-2·5+1= 0 ? 9-10+1=0 ? SI Questió 2 El punt (5,1) no és de la recta r
El punt (3,5) sí és de la recta r
Donats , quines són les components del vector
?
i el vector ?
són iguals els vectors i el
?
No, no són iguals ja que , tenen sentit oposat
Sí tenen la mateixa direcció. Per tant, com a vector director de la recta que passa per A i B podem agafar tant el vector com el
(ja que tenen la mateixa direcció)
Qüestió 3
Quin és el vector director de la recta ?
Recordem que el v.d. de la recta és
Per tant,
el v.d de és
i el pendent m de la recta ?
o bé aïllem y:
o també sabent que el vector director és
Qüestió 4
Quin és el vector director de la recta ?
Recordem que el v.d. de la recta és
Per tant,
el v.d de és
Observació:
Com a vector director de la recta també podem agafar el vector:
ja que té la mateixa direcció que el
, encara que sentit oposat
o el que té la mateixa direcció i sentit que el
, però el mòdul (la longitud) és la meitat.
4. Equacions de la recta
Rectes en el pla
Una recta ve determinada per:
- Dos punts: donats dos punts, existeix una única recta que passa per ells
o bé per:
- Un punt i una direcció: la direcció pot venir donada pel vector director, per l'angle d'inclinació o bé per el pendent de la recta.


Equacions de la recta
Una equació de la recta és una igualtat que verifiquen tots els punts de la recta i només aquests.
Hi ha diferents tipus d'equació de la recta. Depenent de les dades que tinguem, serà més pràctic utilitzar una o altra.
Equació general o implícita
Un vector director de la recta és
si el v.d. és , llavors l'equació de la recta és
Equació explícita
Si en l'equació general aïllem la variable y obtenim:
el coeficient de la x és el pendent de la recta
D'aquesta manera obtenim l'equació:
on m és el pendent de la recta
Observació:
hem dit que si el v.d. és , llavors l'equació de la recta és
aïllant la y tenim:
Per tant,
O sigui, que si el v.d. és
Equació contínua
Si tenim el v.d. i un punt
de la recta, l'equació contínua de la recta és:
Aquest tipus d'equació és molt pràctic quan sabem vector director i punt.
Si voleu més informació o exemples, podeu veure els webs:
Equacions de la recta (on diu "ecuaciones de la recta")
Tipus d'equacions de la recta (a la dreta teniu l'índex per veure els diferents tipus d'equació)
Hem dit que una recta amb vector director té pendent
El vector director ens dóna la direcció de la recta
El pendent de la recta ens dóna la "inclinació" de la recta.
Està clar que la relació entre vector director i pendent és molt estreta.
Si la recta passa pels punts , el seu v.d és el vector que va d'un punt a l'altre
 vector director:
vector director:
Pendent:
Si
el v.d. és
i el pendent és
(i , si recordeu de trigonometria, això és la tangent de l'angle α )
5. Gràfica d'una recta
Per dibuixar una recta, primer de tot heu de tenir clar com representem un punt P(x,y). En aquest enllaç podeu veure la representació de punts en uns eixos de coordenades: Punts i vectors
Com trobem punts d'una recta?
Volem obtenir punts (x,y), o sigui, parells de valors de x i y que satisfacin l'equació de la recta.
Una recta té infinits punts. Podem donar el valor qualsevol a una de les variable i trobar el valor de l'altre variable per tal es satisfaci l'equació.
Exemple 1
Trobem punts de la recta
Podem donar valors a la variable x i trobar el valor de y :
Si Punt
Si
Punt
O podem donar valors a la variable y i trobar el valor de x :
Si
Punt
Exemple 2
recta
Per exemple, podem trobar el punt amb x=0,
Substituïm aquest valor x=o en l'equació:
Per tant tenim el punt
De fet amb trobar dos punts tenim suficient per dibuixar la recta
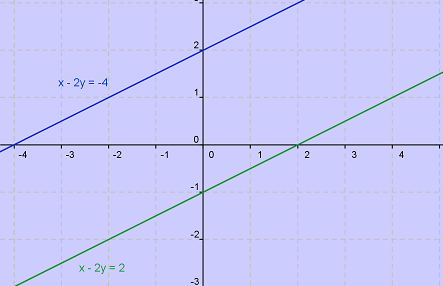
En la taula següent trobem diversos punts de cada recta, donant diferents valors a la x i trobant la y corresponent:

Amb aquest punts de cada recta, dibuixem les rectes:

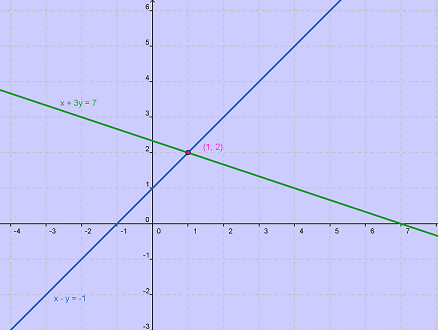
i en aquest enllaç podeu veure com, donat un sistema de dues equacions amb dues incògnites, podem trobar la solució gràficament dibuixant les dues rectes. El punt solució del sistema és el punt de tall (o punt intersecció) de les dues rectes:
6. Exemples trobar equació recta
Exemple 1 Equació general
Trobar la recta que passa pel punt i té vector director
Recordem: El vector director de la recta ax+by+c=0 és (-b,a)
o dit d'altra manera:
v.d. , l'equació general:
Per tant, si el vector director és l'equació de la recta serà de la forma:
I trobem c perquè la recta passi per , que vol dir que ha de complir l'equació:
Per tant l'equació de la recta és:
També podem posar tota l'equació canviada de signe:
Exemple 2 Equació contínua
Trobar la recta que passa pel punt i té vector director
Recordem: vector director , punt
Equació contínua:
Observació: d'aquesta equació podem passar fàcilment a l'equació general de l'exemple 1:
Exemple 3 Equació explícita
Trobar la recta que passa pel punt i té vector director
Recordem: v.d. és
Equació explícita:
Per tant, v.d
L'equació implícita serà de la forma:
Trobem la n sabent que el punt és de la recta:
Per tant:
Exemple 4
Trobar la recta que passa pel punt i té pendent 5.
En aquest cas l'equació més pràctica serà l'explícita:
Com que directament ens donen la dada del pendent, m=5, tenim:
Passa pel punt
Equació de la recta:
o també podem expressar l'equació general que, simplement, és igualant a zero:
7. Equació de la recta que passa per dos punts
Veurem diferents maneres de trobar l'equació de la recta que passa per dos punts:
Exemple 1
Trobeu l'equació de la recta que passa pels punts A(2,1) i B(-3,5)
Volem trobar l'equació del tipus
O sigui, hem de trobar m i n
Que els punts siguin de la recta vol dir que han de verificar l'equació:
Ara tenim plantejat un sistema d'equacions on les incògnites són m i n
Ho fem per reducció, simplement canviem el signe de la 2a equació i sumem les dues equacions:
(m és el pendent de la recta)
I substituint aquest valor en la primera equació 1=2m+n obtenim n:
Per tant, l'equació de la recta és:
Observacions:
- El pendent de la recta és m. Aquesta recta té pendent -4/5
- A partir d'aquesta equació podem obtenir l'equació general de la recta:
Exemple 2
Trobeu l'equació de la recta que passa pels punts A(2,1) i B(-3,5)
Un vector director de la recta serà
Ara amb el v.d i el punt
ja podem expressar l'equació continua:
O si volem l'equació general:
Observacions:
- Fixeu-vos que aïllant la variable y d'aquesta última equació, obtenim l'equació explícita trobada en l'exemple 1.
- Per expressar l'equació explícita hem agafat el punt A, també podríem haver agafat el punt B (el resultat seria el mateix).
8. Posició relativa de dues rectes
Posició relativa de dues rectes
9. Exemples. Posició relativa
Exemples. Posició relativa
EXEMPLE
Donades les rectes:
 que passa per A=(0,1) i B=(3,5)
que passa per A=(0,1) i B=(3,5)
Troba la posició relativa de les dues rectes, i si és el cas doneu les coordenades del punt de tall
I prenem el punt A=(0,1) per escriure l'equació contínua de la recta:
Passem a forma general o implícita.
Recta r, traurem denominadors i l'escriurem en forma ax+by+c=0
-
- Són coincidents?
Comprovarem si les dues rectes són coincidents
Hem de veure si es compleix que:
Observem que aquestes tres fraccions no són iguals i per tant no són coincidents les dues rectes
-
- Són paral·leles?
Són paral·leles si es compleix:
Com que llavors no són paral·leles.
-
- Són secants?
En els apartats anteriors hem vist que no són coincidents, ni paral·leles. Per tant, han de ser secants, o sigui que es tallen en un punt.
Per trobar el punt de tall, cal resoldre el sistema d'equacions format per les dues rectes:
Resolem el sistema d'equacions per qualsevol dels mètodes (substitució, reducció o igualació). Ho farem per reducció.
Multipliquem la segona equació per -2 amb l'objectiu que el coeficient de les x quedi canviat de signe per poder reduir fàcilment
Sumant les dues equacions tenim:
Substituïm aquest valor en la primera equació:
Per tant, les rectes es tallen en el punt
10. Rectes paral·leles, exemple.
Rectes paral·leles, exemple.
EXEMPLE
Donada la recta r, d'equació -3x+4y=11 , i el punt P=(0,-5), es demana:Trobar raonadament l'equació de la recta s , paral·lela a r , que passa per P.
Rectes paral·leles tenen el mateix vector director. Per tant l'equació de les rectes paral·leles a la recta r ha de ser de la forma:
-3x+4y+c=0
Trobem c per tal que la recta passi pel punt P(0,-5) :
Finalment l'equació general de la recta  és : -3x + 4y +20 =0 serviria també qualsevol múltiple d'aquesta equació.
és : -3x + 4y +20 =0 serviria també qualsevol múltiple d'aquesta equació.
Això ho hauríem pogut fer d'altres maneres, per exemple, si volíem obtenir primer l'equació contínua podríem haver fet:
- Trobem el vector director de la recta r, sabem que és (B, -A) és a dir (4, 3).
- Qualsevol recta paral·lela a aquesta té el mateix vector director, per tant la recta que cerquem té el vector director (4, 3) i passa per P=(0,-5)
11. Recta perpendicular
Recta perpendicular
RECTES PERPENDICULARS
Dues rectes són perpendiculars si ho són els seus vectors directors.
Si tenim un vector la forma més ràpida de trobar un vector perpendicular o ortogonal a ells és canviar l'ordre de les components i un d'ells canviar-lo de signe.
Així és perpendicular al vector anterior.
EXEMPLE
Donada la recta r , d'equació 2x+y=7 , i el punt P=(1,0), es demana:
Trobar raonadament l'equació de la recta s, perpendicular a r , que passa per P, i el punt Q on es tallen totes dues rectes.
A partir de l'equació general de r: 2x+y=7 i observant els coeficients de "x" i de "y" es poden obtenir les coordenades del vector normal de r
La recta s vindrà definida pel punt P=(1,0) i aquest vector director (2,1)
Equació contínua de la recta s
Fent càlculs en aquesta equació obtenim l'equació general de la recta s : x - 2y - 1 = 0
Trobem, ara, el punt Q d'intersecció entre la recta s i la recta r:
Es resol el sistema de les dues equacions generals de r i s, per obtenir Q
-
-
- 2x + y = 7
- x - 2y - 1 = 0
-
i resulta ser Q = (3,1)
12. llibre: equació de la recta
Per si voleu una mica més d'explicació de les diverses equacions de la recta i la posició relativa de les rectes.