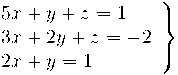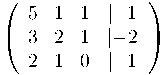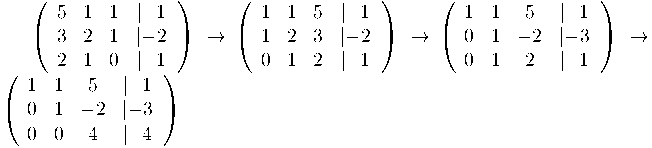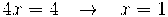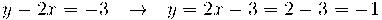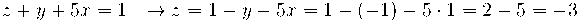LL3_Sistemes d'equacions II
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques aplicades a les C. socials II (Bloc 1) ~ gener 2020 |
| Llibre: | LL3_Sistemes d'equacions II |
| Imprès per: | Usuari convidat |
| Data: | dimecres, 26 de juny 2024, 10:02 |
Descripció
Dubtes freqüents Sistemes d'equacions
1. Classificació d'un sistema d'equacions: Teorema de Rouché-Frobenius
Donem un criteri per classificar un sistema d'equacions lineals.
Donat un sistema d'equacions lineals, sigui
M la matriu associada al sistema
M' la matriu ampliada
Donem un criteri per classificar un sistema d'equacions lineals.
Teorema de Rouché-Frobenius:
Exemples:
Classifiqueu el sistema:
Esglaonem la matriu ampliada per tal de calcular els rangs de la matriu associada i de l'ampliada:
Recordem que el rang d'una matriu, un cop esglaonada, és el nombre de files no nul·les:
Classifiqueu el sistema:
Esglaonem la matriu ampliada per tal de calcular els rangs de la matriu associada i de l'ampliada:
Recordem que el rang d'una matriu, un cop esglaonada, és el nombre de files no nul·les:
Per tant:
rango 2 < 3 nombre incógnites Sistema compatible indeterminat
2. Canvi de files o columnes en la matriu associada a un sistema d'equacions.
En la matriu associada a un sistema podem canviar l'ordre de les files sense cap repercussió (ja que l'ordre de les equacions en un sistema és irrellevant, si canviem d'ordre les equacions obtenim un sistema equivalent, és a dir, amb les mateixes solucions).
Si ens interessa també podem canviar l'ordre de les columnes però al fer això hem de pensar que estem canviat les incògnites que hi ha en cada columna. Vull dir, si per exemple tenim el sistema d'equacions:
Si volem fer un intercanvi de les columnes 1 i 3 ja que pensem que d'aquesta manera ens és més fàcil esglaonar la matriu, el podem fer però tenint en compte que ara en la 1a columna tindrem els coeficients de la z, i en la 3a columna els de la x (ho hem de recordar al acabar d'esglaonar):
ara al resoldre el sistema començant per l'última fila (recordem que amb el canvi fet en la 3a columna tenim les x), tenim:
en la 2a fila tenim:
i finalment substituint en la 1a fila:
Observació: el canvi de columnes es pot fer entre columnes de la
matriu de coeficients, no amb la columna dels termes independents de la
matriu ampliada.
3. Solucions d'un sistema compatible indeterminat
Discussió i resolució de sistema compatible indeterminat.
Exemple 1
Mètode de Gauss. Esglaonem:
Discussió (classificació):
(Teorema Rouché-Fröbenius)
rang matriu coeficients = rang matriu ampliada = 2 => compatible
rang = 2 < nombre d'incògnites = 3 => compatible indeterminat
les infinites solucions es poden expressar en funció d'1 paràmetre (ja que la diferència entre el nombre d'incògnites i el rang és 1)
Solució:
Començant per la 2a equació:
agafarem z com el paràmetre λ z= λ
substituint en la 1a equació tenim:
Per tant les solucions són
( es llegeix "per a tot
pertanyent als reals", vol dir simplement que
pot ser qualsevol nombre real)
Vídeo
En aquest vídeo podeu veure la resolució d'aquest mateix exercici:
4. Determinats d'ordre 2 o 3.
La forma més pràctica de calcular un determinant d'ordre 2 o 3 és aplicant la Regla de Sarrus.
(recordeu que només es pot calcular el determinant d'una matriu quadrada (igual nombre de files que columnes).
Determinant d'una matriu 2x2
Exemple
Determinant d'una matriu 3x3
Exemple:
Calcular el determinant de la matriu
vídeo on podreu veure més clarament com es calcula:
5. Matriu inversa
Calculem la inversa de la matriu
Ho fem de 3 maneres diferents.
(Per matrius 3x3 seria similar però quedarà una mica més llarg d'operacions)
- Utilitzant el determinant i els adjunts de la transposada.
Calcular la inversa de
Calculem el determinant
Considerem la transposada de la matriu A:
i la matriu d'adjunts de :
Per tant:
· Plantejant un sistema d'equacions:
Calcular la inversa de
Volem una matriu X tal que
És a dir:
Per tant:
· Pel mètode de Gauss-Jordan
Calcular la inversa de
De fet és el mateix que hem fet a dalt però ho expressem en forma matricial.
Es tracta de plantejar la matriu ampliada formada per la matriu i la matriu identitat. És a dir:
Hem de fer transformacions elementals fins que en la part esquerra ens quedi la matriu identitat:
Per tant: