Conceptes bàsics Anàlisis II
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques (autoformació IOC) |
| Llibre: | Conceptes bàsics Anàlisis II |
| Imprès per: | Usuari convidat |
| Data: | dissabte, 4 de maig 2024, 18:48 |
Taula de continguts
- 1. APLICACIONS DE LES DERIVADES
- 2. INTEGRALS. APLICACIONS
- 3. Introducció a la integració
- 4. Concepte de integració.
- 5. Taula integrals immediates
- 6. Integral indefinida. Primitives
- 7. Propietats de les integrals
- 8. Com aplicar les propietats anteriors
- 9. Funcions que es poden reduïr a potències
- 10. Integració per canvi de variable.
- 11. Mètode integració per parts
- 12. Com sabem en la integració per parts qui és u i qui dv
- 13. Integrals on hi ha un logaritme
- 14. Integrals definides
- 15. Càlcul d'integrals definides
- 16. Concepte d'integral definida
- 17. Càlcul d'àrees sota una corba
- 18. Exemple 2. Àrea sota una corba
- 19. Exemple 3. Integral definida
- 20. Càlcul àrea entre dos corbes
- 21. Càlcul àrea entre dos corbes. Exemple 2
- 22. Aplicacions en altres camps del coneixement
- 23. Dossier amb exercicis resolts
- 24. Exercicis PAU
- 25. Exercicis PAU
APLICACIONS DE LES DERIVADES
Optimitzar és trobar el màxim o el mínim d'una funció sotmesa a certes condicions imposades.
Per resoldre un problema d'optimització seguirem aquests passos:
- Identificar les variables del problema.
- Escriure algebraicament la funció que s'ha d'optimitzar
- Escriure algebraicament la relació entre les variables
- Aïllar de la relació anterior una variable i substituir en la funció. Cal aconseguir que la funció sigui d'una única variable.
- Trobar els extremes (màxims i mínims) de la funció, resolent l'equació f '(x) =0
- Comprovar si són màxims o mínims
- Analitzar la coherència de la solució dins del context de l'enunciat
Exemple 1
Aquest dipòsit en forma d'ortoedre, té un volum de 72 m3 i la llargada (a) és el doble que l'amplada (c). Deduir les dimensions del dipòsit per tal que la superfície sigui mínima
- Identificar les variables del problema.
a= llarg
b= ample
c= altura
- Escriure algebraicament la funció que s'ha d'optimitzar
Àrea(A)= 2 bases + 4 cares laterals = a·c + a·c + b·c + b·c +a·b +a·b = 2·a·c + 2·b·c + 2·a·b
- Escriure algebraicament la relació entre les variables
V=llarg·ample·altura = a·b·c
72 = a·b·c
A més la llargada (a) és el doble que l'amplada (c)
a = 2·c
De les dues equacions obtenim :
72 = 2c·b·c = 2bc2
null
- Aïllar de la relació anterior una variable i substituir en la funció.
A = 2·a·c + 2·b·c + 2·a·b = 2·(2c)·c + 2·b·c + 2·(2c)·b =4c2 + 2·b·c + 4bc =4c2 + 6·b·c
- Trobar els extremes (màxims i mínims) de la funció, resolent l'equació f '(x) =0
- Comprovar si són màxims o mínims
Es pot comprovar de dos formes.
En aquest exercici comprovarem en la segona derivada.
Si f ''(punt) >0 ---> el punt és mínim
Si f ''(punt) <0 ---> el punt és màxim
En el nostre cas, calcularem la segona derivada
Per tant en c= 3 la funció presenta un mínim
- Analitza
El resultat té sentit ja que hem obtingut un ortoedre de dimensions c= 3 cm, a=6 cm i b=36/c2= 36/9 =4 cm
Exemple 2
De tots els triangles rectangles d'hipotenusa 10 cm , trobeu la longitud dels catets del triangle que té perímetre màxim. Comproveu que la solució trobada correspon realment al de perímetre màxim.
- Identificar les variables del problema.
x= catet (base del triangle) y= catet (altura del triangle)
- Escriure algebraicament la funció que s'ha d'optimitzar
Perímetre màxim. Per tant la funció a maximitzar és el perímetre.
P = Perímetre = Suma de tots els costats = x+ y +10
- Escriure algebraicament la relació entre les variables
La relació entre les variables és el Teorema de Pitàgores: x2+ y2 = 102
- Aïllar de la relació anterior una variable i substituir en la funció. Cal aconseguir que la funció sigui d'una única variable.
- Trobar els extremes (màxims i mínims) de la funció, resolent l'equació f '(x) =0
Cal derivar la funció P(x) d'una variable
- Comprovar si són màxims o mínims
Els valors negatius no els tindrem en compte donat que no poden correspondre a la mida dels catets d'un triangle rectangle.
- Analitzar la coherència de la solució dins dels context de l'enunciat
El resultats
tenen sentit en el context del problema. Observeu que el triangle de màxim perímetre és el triangle isòsceles, que té el dos catets iguals.
Les vendes anuals S d'un nou producte s'expressen segons aquesta fórmula:
a) Completa la taula següent
| x | 0.5
|
1
|
1.5
|
2
|
2.5 | 3 |
|---|---|---|---|---|---|---|
| S |
b) En quin moment concret les vendes van ser les màximes?
Resposta
Ja es veu que a mida que va passant el temps, va creixent el nombre d'articles venuts. En l'interval [0,3] sembla que el màxim s'obtindrà en x=3
Estudiem la derivada per saber si hi ha un extrem en l'interval [0,3]. Si no hi ha cap extrem, vol dir que el mínim i màxim de la funció serà o en x=0 o en x=3
Veiem que si hi ha un extrem (màxim o mínim) relatiu ha d'estar en x=0
S(0) = 0 articles. Correspon al mínim
El màxim per tant està en x=3.
|
Exercici 1.
Aquesta expressió
a) Trobeu la funció B(x) que expressi el benefici obtingut per la venda de "x" unitats. Els Beneficis s'obtenen de restar els ingressos menys les despeses.
b) Calculeu el nombre d'unitats que cal fabricar per obtenir el màxim de beneficis. c) Quin és el preu per unitat òptim? |
Recordeu els passos:
- Identificar les variables del problema.
- Escriure algebraicament la funció que s'ha d'optimitzar
- Escriure algebraicament la relació entre les variables
- Aïllar de la relació anterior una variable i substituir en la funció. Cal aconseguir que la funció sigui d'una única variable.
- Trobar els extremes (màxims i mínims) de la funció, resolent l'equació f '(x) =0
- Comprovar si són màxims o mínims
- Analitzar la coherència de la solució dins del context de l'enunciat
- Pas 1. Identificar les variables x=nombre d'unitats venudes d'un producte. Només hi ha una variable.
- Pas 2. Escriure algebraicament la funció que s'ha d'optimitzar. Observeu que la funció f(x) no és la funció a optimitzar. S'ha d'optimitzar el benefici
- Pas 3 i Pas 4 no s'han de fer, ja que només hi ha una variable
- Pas 5 Trobar els extrems de la funció B(x)
- Pas 6 Comprovar si són és màxim o mínim. Podem usar la segona derivada.
- Analitzem la coherència del resultat. Encara que s'han obtingut dos resultats només el resultat positiu té sentit.
Exercici :
Trobeu les dimensions del rectangle inscrit en un cercle de radi 1m, que tingui l'àrea màxima.
Per tal de donar resposta us adjuntem la figura que il·lustra la situació.
També explicitem els passos a seguir:
- a) Assigneu incògnites. En aquesta cas ja les hem explicitat en el gràfic.
- b) Escriviu l'àrea del rectangle en funció de "x" i "y"
- c) Escriviu la relació entre les incògnites x, y, usant el Teorema de Pitàgores.
- d) Aïlleu "y" (es podria aïllar l'altra incògnita)
- e) Escriviu ara, l'àrea del rectangle en funció de només la incògnita "x"
- f) Calculeu el màxim, derivant la funció (d'una sola variable) obtinguda en l'apartat anterior.
Resolució:
a) x= alçada del rectangle i y= base del rectangle
b) Àrea del rectangle = x·y
c) Relació entre "x" "y" i la diagonal del cercle, tenint en compte que es pot aplicar el Teorema de Pitàgores, donat que la base, l'altura i la diagonal formen un triangle rectangle-->
d)
e)
f)
Faltaria argumentar per què aquests valors corresponen a l'àrea màxima i no a l'àrea mínima.
Establirem intervals i estudiarem el signe de la derivada i el creixement de la funció per saber si "x" és màxim o mínim
| valor x
|
|
|
|
| signe A '
|
A ' (1) = +
|
A '(2) = -
|
|
| creixement de
la funció A |
creixent | màxim | decreixent |
Per tant en x=
Solució : El rectangle d'àrea màxima que es pot inscriure en el cercle de radi 1, és un QUADRAT de costat
Trobar els valors de "a" i "b" per tal que la funció f(x) passi pels punts A(0,2) i B(2,0) i en A tingui un màxim :
Resolució:
Cal traduir les condicions del problema a equacions
a) f(x) passa per A --> f(0)=2 -->
b) f(x) passa per B --> f(2)=0 -->
c) f(x) té un màxim en A --> f ' (0)=0 -->
Calculeu els valors dels paràmetres: a, b i c per tal que la funció f(x) compleixi aquests requisits:
- Tingui un extrem relatiu en el punt d'abscissa x=1
- La recta tangent a la funció f(x) en x=0 sigui la recta
S'ha de traduir les condicions del problema a equacions.
Aquí cal veure que el pendent de la recta tangent coincideix amb la derivada en el punt x=0. La recta tangent té pendent m=1 per tant f ' (0)=m=1. Per una altra banda si x=0 el valor de y en la recta és y=0+3=3, per tant el punt on coincideixen la recta tangent i la funció f(x) és en el punt (0,3)
Introducció a la integració
La derivació i la integració són dos procediments matemàtics molt potents i útils en la resolució d'una infinitat de problemes. Aquests dos procediments són la base del Càlcul infinitesimal.
La integració permet calcular àrees i volums de cossos geomètrics i resoldre problemes d'altres àmbits, com ara l'Economia i la Física.
En aquest recurs trobareu un resum dels conceptes bàsics sobre integració i exemples d'aplicació.
S'explica com:
- Calcular la funció primitiva d'una funció
- Calcular integrals immediates i quasiimmediates
- Calcular integrals pels mètodes d'integració de substitució i parts
- Calcular integrals de funcions racionals senzilles
- Calcular integrals definides
- Calcular àrea de la regió del pla compresa entre dos funcions
- La integral permet resoldre situacions de la vida real.
Concepte de integració.
La integració.
La integració es pot definir com el procés invers a la derivació. Així doncs calcular la integral d'una funció f (x) és trobar una altra funció g (x) de forma que g ' (x) = f (x)
L'expressió: es
llegeix com la integral de la funció f(x) respecte la variable x.
Per calcular integrals, cal saber bé derivar, i tenir interioritzades les derivades de les funcions més usuals
Exemple
Posem aquesta K, que vol dir que qualsevol nombre va bé.
Dit d'una altra forma :
Observeu que si derivem la funció g(x) = x + k obtenim g ' (x) = 1
Per tant es compleix la idea de que fer la integral de f(x) és buscar una funció g(x) que al derivar-la dona g ' (x) = f(x)
Exemple
Observeu que si derivem la funció g(x) =
obtenim g ' (x) = x
Exemple
Observeu que si derivem la funció g(x) =
obtenim g ' (x) = x2
Exemple
Observeu que si derivem la funció g(x) =
obtenim g ' (x) = x3
Taula integrals immediates
Taula d'integrals immediates
Aquesta taula permet calcular les integrals immediates. La taula es construeix a partir de la taula de derivades.
| Primitives immediates | Primitives immediates
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Primitives immediates trigonomètriques |
|
Primitives immediates trigonomètriques
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Integral indefinida. Primitives
Integral indefinida. Primitiva. Diferències entre els dos conceptes.
La primitiva d'una funció és una única. La integral indefinida són moltes.
- Una funció F(x) és una primitiva d'una funció f(x) quan F '(x)=f(x)
- Integral indefinida d'una funció f(x) és el conjunt de totes les primitives de f(x)
Per exemple les funcions són primitives de la funció
ja que al derivar-les ens dona f(x):
Però hi ha moltíssimes més funcions que són primitives de f(x). Qualsevol funció que sigui del tipus on C pot ser qualsevol nombre real
serà una primitiva.
Al conjunt de totes les primitives de la funció f(x) l'anomenem integral indefinida i es representa
Per tant el conjunt de totes les primitives de la funció bé representat per la integral
definida
En aquest exemple us mostrarem la diferència entre trobar una primitiva d'una funció i trobar la integral indefinida de la funció.
Trobeu la integral indefinida de la funció f(x)
Trobeu la primitiva de la funció que passi pel punt A=(-1,6)
Fins aquí s'ha trobat la integral indefinida de la funció f(x), ja que hem trobat totes les funcions G(x) que en derivar-les dona f(x)
Ara es buscarà l'única primitiva que passa pel punt A=(-1,6)
G(x) ha de passar per A=(-1,6) per tant G(-1)=6
Conclusió:
La integral indefinida de la funció f(x) és:
La primitiva de la funció que passa pel punt A=(-1,6) és:
Propietats de les integrals
Quines propietats puc aplicar en el càlcul d'integrals i quines no?
Les úniques propietats que són vàlides i per tant podem utilitzar són :
En cap cas són vàlides les igualtats :
Com aplicar les propietats anteriors
Com puc aplicar les propietats anteriors?
Propietat 1:
Utilitat 1 : quan un nombre que està multiplicant a tota la funció ens interessa que no estigui dins la integral ja que la coneixem
Exemples :
Utilitat 2 : quan ens interessaria que hi hagi un nombre que està multiplicant a tota la funció perquè sapiguem resoldre la integral
Exemples :
En aquest cas ens interessava tenir un "5" dins de la integral ja que sabem que:
En aquest exemple ens interessava tenir un "2" dins de la integral ja que sabem que:
En aquest exemple ens interessava tenir un "3" dins de la integral ja que:
Propietat 2 i 3:
Utilitat : quan sabem resoldre la integral per separat de cada funció
Exemples :
I ara acabem amb exemples que combinen les tres propietats
Exemples :
Funcions que es poden reduïr a potències
Com puc fer més fàcil el càlcul d'algunes integrals?
Hi ha funcions que abans de integrar-les és millor que fem un petit retoc en la seva expressió. Aquest és el cas d'una funció que la seva expressió es pot reduir a una sola potència o a suma o resta de potències.
Si tenim expressada la funció de la manera sempre serà més fàcil ja que
Exemple 1:
Imagina que hem d'integrar la funció .
Fixem-nos que
Aleshores
Exemple 2:
Ens demanen .
La manera més senzilla de fer aquesta integral és primer arreglant l'expressió de la funció abans d'integrar
Ara resolem ja la integral
Exemple 3:
També podem utilitzar aquesta tècnica per integrar funcions racionals quan el denominador estigui format per un sols monomi
És per exemple el cas de la funció .
Primer separem l'expressió en tants trossos com termes te el numerador i després reduïm cada tros a una potència
Ara resolem ja la integral
Integració per canvi de variable.
Exemple 1.
Ara substituïm en la integral inicial :
Observeu que aquesta integral es podria plantejar com quasi immediata, obtenint el mateix resultat.
Mètode integració per parts
Mètode d'integració per parts
És un mètode molt útil en la integració de funcions que són el producte (multiplicació) d'altres funcions. Consisteix en separar la funció a integrar en dues parts. Una part s'anomenarà u i l'altra dv. I s'aplicarà la següent fórmula:
Mètode
Encara que és un mètode simple cal aplicar-lo correctament. Observeu que després d'aplicar el mètode d'integració per parts, cal resoldre una segona integral, que necessàriament ha de ser més fàcil que la primera i si no és així, és que s'han triat
incorrectament les parts.
Passos a seguir:
-
L'integrant (funció inicial) ha de ser producte (multiplicació) de dues funcions (factors).
-
Un dels factors serà u i l'altra dv.
-
S'ha de calcular du derivant l'expressió u
-
S'ha de calcular v integrant dv.
-
S'ha d'aplicar la fórmula.
- S'ha de resoldre la integral que queda.
Pas 2, 3, 4.Triar quina funció serà la que faci de u (funció a derivar) i la que faci de dv (funció a integrar)
Aquesta no és una decisió fàcil. Cal pensar que integrar és més difícil i per tant s'ha de triar pensant en quina funció és millor integrar i si en coneix la integral.
En aquest cas la funció Logaritme (Ln(x)) es pot derivar fàcilment però no és immediat trobar la serva integral. Això fa pensar que les parts han de ser:
Pas 5,6. Aplicar la fórmula i resoldre la integral que queda després d'aplicar la fórmula.
Com sabem en la integració per parts qui és u i qui dv
En la integració per parts com sabem quin dels dos membres és u i quin és dv? u és sempre el primer?
No és sempre u el primer factor. L'ordre no determina l'elecció. Normalment procedim de la següent manera:
- Si els dos factors que s'estan multiplicant els se integrar i un dels dos és un polinomi, llavors agafem com a u el polinomi. D'aquesta manera en la integral que queda surt el grau rebaixat i per tant una integral més senzilla. per exemple:
Ara tornaríem a fer el mateix amb la integral que ens queda que com veus és del mateix estil però on el polinomi és d'un grau menor
- Si sols sabem integrar un dels dos factors llavors, aquest és dv. Per exemple
- De vegades no en sap integrar cap i sols hi ha un factor. En aquest cas afegim la funció 1 multiplicant i aquesta serà la funció a derivar. Per exemple
- Si se sap integrar les dues funcions, en principi s'ha de provar de les dues maneres i escollir la que doni lloc a una integral més senzilla.
Integrals on hi ha un logaritme
Si quan busquem la primitiva d'una funció en aquesta hi ha un In x (logaritme neperià de x) aquest té alguna integral indefinida immediata? Com es resol?
No hi ha un mètode directe. Depèn de la integral si és quasi immediata o si es fa per canvi de variable, o per parts o altres mètodes que no estudiareu en aquest curs.
Abans heu vist un exemple que contenia un logaritme i que s'ha resolt per parts. Ara us mostrem un exemple on aplicarem canvi de variable i integral quasi-immediata.
Exemple:
Com a integral quasi-immediata:
Fixeu-vos que si s'arregla l'expressió de la funció a integrar s'adequa a aplicar que
Hem inserit un 2 que necessitava ja que .
De fet s'ha multiplicat per 1 =2/2 I PER TANT queda igual .
Ara ja podem finalitzar la integral
Per canvi de variable:
Integrals definides
- Càlcul d'integrals definides
- Concepte d'integral definida
- Càlcul d'àrees sota una corba
Càlcul d'integrals definides
Com es calcula una integral definida?
Si f(x) és contínua en [a,b] i G(x) és una primitiva seva, aleshores:
Exemple 1:
Exemple 2:
Primer busquem una primitiva de la funció.
Observem que i per tant és una integral immediata
Ara ja podem resoldre la integral definida
Exemple 3:
Primer busquem una primitiva de la funció.
Observem que i per tant és una integral immediata
Ara ja podem resoldre la integral definida
Concepte d'integral definida
Què representa fer una integral definida?
La integral definida representa fer una suma i restes d'àrees compreses entre la gràfica de la funció, l'eix d'abscisses i les rectes x=a i x=b, tenint en compta que si l'àrea queda per sota de l'eix de les X és resta i si queda per sobre es suma
Per exemple si tenim una funció la gràfica de la qual és la de sota, tindríem que
Comprovem això amb un exemple concret
Exemple 1:
Calculem primer la integral definida de la funció f(x)=x-1 amb límits d'integració x=-2 i x=3 (per la regla de Barrow)
Ara comprovem aquest resultat amb el càlcul de la suma o resta d'àrèes
Càlcul d'àrees sota una corba
Com trobar l'àrea compresa entre la gràfica d'una funció, l'eix OX i dues abscisses?
Per trobar una àrea compresa entre la gràfica d'una funció f(x), l'eix d'abscisses i les rectes x=a i x=b cal seguir els passos
1. Trobar els punts de tall de la gràfica de la funció amb l'eix d'abscisses resolent l'equació f(x)=0
2. Seleccionar d'entre els punts de tall obtinguts, aquells que es trobin en l'interval [a,b]. Imaginem que aquests són x1, x2 , x3 i x4
3. L'interval [a,b] queda dividit en altres intervals si col·loquem els valors anteriors : [a, x1], [x1, x2], [x2, x3], [x3, x4] i [x4, b]
4. Per a cada interval trobat hem d'esbrinar si la gràfica de la funció queda per sobre l'eix OX o per sota
5. En funció de si l'àrea obtinguda queda per sobre o per sota caldrà agafar la integral definida o canviar-li el signe.
Per exemple en el cas:
Exemple 1 :
Anem a trobar l'àrea compresa entre la gràfica de la funció , l'eix d'abscisses i les rectes x = -2 i x = 1'5
1.
2. Dels valors obtinguts agafem els valors x = -1 i x = 1
3. L'interval [-2,1'5] queda dividit en 3 intervals: [-2,-1], [-1,1] i [1,1'5] i per tant tindrem 3 àrees també:
4. Per a cada interval trobat hem d'esbrinar si la gràfica de la funció queda per sobre l'eix OX o per sota. Per això busquem la imatge d'un valor de cada interval:
5. Calculem el valor de les diferents àrees i finalment les sumem: Per fer els càlculs el més exacte possible posarem 1,5= 3/2
Exemple 2. Àrea sota una corba
Exercici:
Calculeu l'àrea del recinte entre la corba i l'eix d'abscisses (eix OX)
Resolució:
Per trobar una àrea compresa entre la gràfica d'una funció f(x), i l'eix d'abscisses , cal seguir els passos
1. Trobar els punts de tall de la gràfica de la funció amb l'eix d'abscisses resolent l'equació f(x)=0
2. Suposem que els punts de tall corresponen a x1, x2 , x3 i x4
3. Els intervals on treballarem seran: [x1, x2], [x2, x3], [x3, x4]
4. Per a cada interval trobat hem d'esbrinar si la gràfica de la funció queda per sobre l'eix OX o per sota
5. En funció de si l'àrea obtinguda queda per sobre o per sota caldrà agafar la integral definida o canviar-li el signe.
Anem a trobar l'àrea compresa entre la gràfica de la funció , i l'eix d'abscisses.
1.
2. Els 2 intervals, en els que treballarem són: [-1,0], [0,1] i per tant tindrem 2 àrees també:
3. Per a cada interval trobat hem d'esbrinar si la gràfica de la funció queda per sobre l'eix OX o per sota. Per això busquem la imatge d'un valor de cada interval:
- f(-0,5) = negatiu --> f(x) és negativa en l'interval [-1,0)
- f(0) = 0
- f(0,5) = negatiu --> f(x) és negativa en l'interval (0,1]
Àrea =
Com és una àrea cal prendre el resultat en valor absolut. Per tant
Exemple 3. Integral definida

Càlcul àrea entre dos corbes

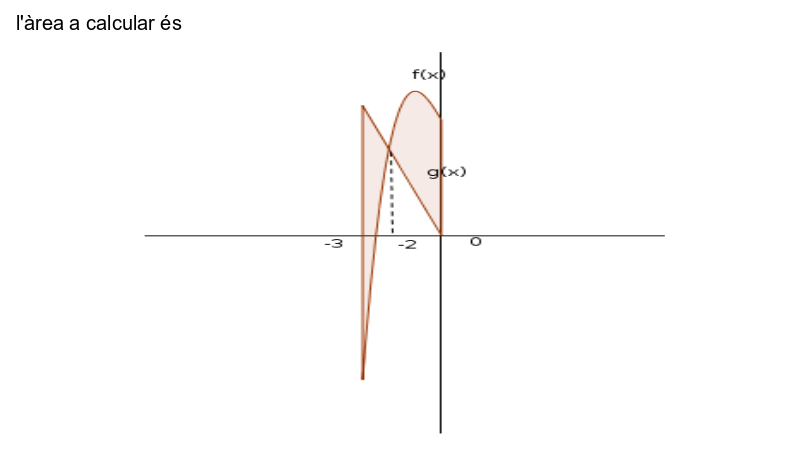
El primer pas que s'ha de fer és trobar els punts d'intersecció entre les dues corbes, resolent el sistema d'equacions:
Àrea = [Àrea compresa entre les dues funcions i x=-3 i x=-2] + [Àrea compresa entre les dues funcions i x=-2 i x=0]
Recordant que un àrea ha de ser sempre positiva.
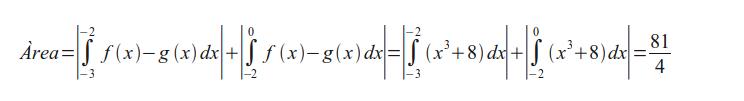
Càlcul àrea entre dos corbes. Exemple 2
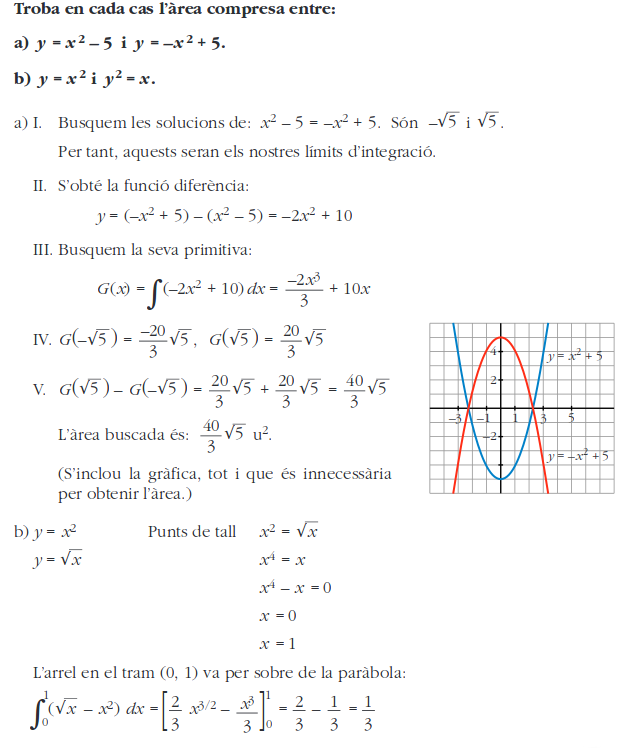
Aplicacions en altres camps del coneixement
Aplicació en el medi ambient
S'anomena "cabal" a la velocitat que porta l'aigua d'un riu. En general, el cabal va en funció dels mesos de l'any. A l'hivern els rius porten més aigua que a l'estiu.
La quantitat d'aigua que passa per un riu durant un període de temps és igual a l'àrea compresa entre la corba , l'eix X i l'interval de temps corresponent.
En aquest exemple imaginem que el cabal de riu segueix aquesta funció:
on :
ve donat en milers de hectolitres per segon i
ve donat en mesos
Quina quantitat d'aigua passa pel riu durant 1 any?
Resposta:
La gràfica de la funció f(t) és aquesta:

Trobar el cabal del riu al llarg de tot l'any, significa calcular l'àrea sota aquesta corba. Per tant cal integrar la funció donada.
Cabal anual =
a) Primer cal calcular la integral indefinida (sense tenir en compte els límits d'integració)
b) Després substituir la funció obtinguda en els límits d'integració
c) Restar els valors i veure si té sentit el resultat.
a)
b)
c) Restem F(12)-F(0)
Per tal de tenir una idea de la quantitat d'aigua 34.88 milers de hl per segon = 34880 hl/s = 3 488 000 l/s (litres per cada segon, durant 1 any) Guau !
Dossier amb exercicis resolts
Exercicis PAU
Exercici|
Sigui la funció
a) La primitiva de la funció
b) L'àrea limitada per la funció |
Recordeu els passos:
- Integrar la funció, pel mètode que es trobi més oportú.
- Aplicar la Regla de Barrow per calcular la integral definida.
- Analitzar la coherència de la solució. Recordeu que les àrees no poden ser negatives i en aquests casos cal fer el valor absolut de la solució.
Resolució:
a) Aquesta integral es pot fer pel mètode del canvi de variable.
Podeu provar diversos canvis, però el que millor funciona és:
Apliquem el canvi a la integral:
b) La funció sin(x) i la funció cos2(x) són positives en l'interval , per tant no talla l'eix OX, i per això l'àrea correspon a aquesta integral definida:
Exercicis PAU
|
Exercici 1.
Considereu les funcions:
a) Feu un esbós de la regió limitada per les seves gràfiques i l'eix de les abscisses i la recta x=e=2,7. Calculeu el punt de tall entre les dues funcions.
b) Calculeu l'àrea de la regió descrita en l'apartat anterior. |
Recordeu els passos:
- Trobar els punts de tall entre les gràfiques de f(x) i g(x).
- Integrar la funció f(x) i la funció g(x).
- Aplicar la Regla de Barrow per calcular la integral definida entre els valors trobats.
- Analitzar la coherència de la solució dins del context de l'enunciat.