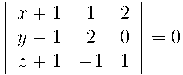Dubtes freqüents sobre geometria
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques (autoformació IOC) |
| Llibre: | Dubtes freqüents sobre geometria |
| Imprès per: | Usuari convidat |
| Data: | diumenge, 5 de maig 2024, 00:00 |
Descripció
.
Taula de continguts
- VECTORS
- GEOMETRIA AFÍ
- Rectes en l'espai
- Punt i vector d'una recta donada en forma implícita
- Components d'un vector
- Equacions d'un pla
- Vector normal d'un pla
- Feix de plans
- Posicions relatives entre dos plans
- Posició relativa entre recta i pla
- Com trobar el punt d'intersecció d'una recta i un pla (en cas que es tallin)
- Posició relativa entre dues rectes
- MÈTRICA A L'ESPAI
VECTORS
.
Punts alineats
Com sé si 3 punts formen un triangle o estan alineats?
"3 punts A, B, C no formen un triangle si estan alineats".
Si dibuixem 3 punts A, B i C que estan alineats (o sigui, sobre una mateixa recta), i dibuixem els vectors podem veure que aquests vectors tenen la mateixa direcció (o sigui, són paral·lels).
Recordem la condició de paral·lelisme (en qualsevol dimensió):
La condició de paral·lelisme de dos vectors és que les components dels vectors siguinón proporcionals, o sigui, que els vectors són linealment dependents:
Això ho llegim així : dos vectors són paral·lels si i només si les seves components són proporcionals, o si i només si són linealment dependents
o bé: dos vectors són paral·lels és equivalent a dir que les seves components són proporcionals i equivalent a dir que són linealment dependents.
(Aquesta condició és la mateixa per components de vectors del pla, amb 2 components).
El que volem és que els 3 vectors siguin paral·lels, o sigui dependents dos a dos, per tant el rang dels 3 vectors ha de ser 1.
o en dimensió 3 també podem dir:
Angle entre vectors
Angle que formen dos vectors
Per trobar l'angle que formen dos vectors
donats per les seves components, utilitzem el producte escalar:
i tenint el valor de del cosinus, amb la funció arc cosinus trobem l'angle
(la funció encara que molts de vosaltres escriviu cos-1, és més correcte escriure arccos)
El que vull destacar és que prenem el producte escalar amb el signe que surti.
Angle que formen dues rectes de vectors directors
És diferent quan calculem l'angle entre dues rectes (ho farem en els següents lliuraments), perquè llavors si és pren l'angle més petit que formen, i llavors en la fórmula agafem el valor absolut del producte escalar.
Vectors perpendiculars
La condició perquè dos vectors siguin perpendiculars és que el seu producte escalar sigui 0.
(ho llegim així: dos vectors són perpendiculars és equivalent a dir que el seu producte escalar és 0)
Aquesta condició surt directament de la fórmula per trobar l'angle que formen 2 vector, ja que si són perpendiculars, l'angle que formen és de 90º, i cos 90l' = 0 però la destaco aquí per la importància de la condició.
Dependència-independència entre vectors
Referent a dependència- independència de vectors, base de l'espai,...... tingueu clares aquestes proposicions:
----------------------------------------------------------------------------------------------------------------------------------------------
Siguin 3 vectors v1, v2, v3 de l'espai
v1, v2, v3 linealment independents rang {v1, v2, v3} = 3
det(v1,v2,v3)
0
O, el que és mateix:
v1, v2, v3 linealment dependents rang {v1, v2, v3} < 3
det(v1,v2,v3)=0
----------------------------------------------------------------------------------------------------------------------------------------------
Siguin v1, v2, v3 vecors de l'espai
v1, v2, v3 formen base de R3 v1, v2, v3 linealment independents
rang {v1, v2, v3} = 3 det(v1,v2,v3)
0
O, el que és mateix:
v1, v2, v3 no formen base de R3 v1, v2, v3 linealment dependents
rang {v1, v2, v3} < 3
det(v1,v2,v3)=0
----------------------------------------------------------------------------------------------------------------------------------------------
4 vecors de l'espai (de R3) sempre són linealment dependents
Més general:
En l'espai, un conjunt de més de 3 vectors sempre és linealment dependents.
--------------------------------------------------------------------------------------------------------------------------------------------------
Qualsevol base de R3 està formada per 3 vecors linealment independents
-------------------------------------------------------------------------------------------------------------------------------------------------
Repàs vectors de 2 i 3 dimensions
Els vectors de (2 dimensions, geometria en el pla) s'han estudiat en cursos anteriors.
Aquí teniu uns enllaços en cas que vulgueu repassar alguna cosa dels vectors:
Vectors de :
Vectors de
GEOMETRIA AFÍ
.
Rectes en l'espai
Donats
vector director
Punt
Equació vectorial
Equació paramètrica
Equació contínua
Equació implícita
Exemple
Equacions de la recta que passa pel punt i té vector director
Equació vectorial:
Equació paramètrica
Equació contínua:
Equació implícita
l'obtenim de l'anterior:
Observació: si tenim l'equació implícita d'una recta, per saber punt i vector director veieu:
Punt i vector d'una recta donada en forma implícita
Veiem diferents maneres de trobar un punt i un vector director d'una recta donada en equació implícita
</p>
<p><br />Una de les maneres més senzilles de trobar un vector director de la recta és fent el producte vectorial dels vectors normals dels plans que determinen la recta. O sigui:</p>
<p>vector director:
</p>
<p>i per trobar un punt, donem un valor qualsevol a una variable i, resolem el sistema per trobar les altres dues variables.</p>
<p></p>
<p><span style="text-decoration: underline;"><strong>Exemple.</strong></span></p>
<p>recta</p>
<p>
</p>
<p></p>
<p><strong>vector director:</strong>
</p>
<p>Fem aquest producte vectorial:</p>
<p>
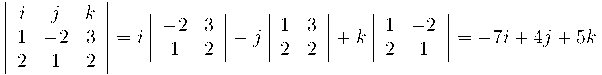
Per tant, un vector director de la recta és (-7,4,5)
Fixeu-vos que tant podem agafar el vector (-7,4,5) com el (7,-4,-5)
Punt.
Donem un valor qualsevol a una de les variables.
Agafem, per exemple z=0
Per trobar les coordenades x, y hem de resoldre el sistema:
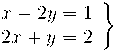
la solució d'aquest sistema és x=1, y=0
Per tan, un punt de la recta és (1,0,0)
-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Podeu veure en aquest vídeos dos mètodes més per trobar un punt i un vector director de la recta:
a) Trobant dos punts de la recta:
b) Trobant l'equació paramètrica de la recta:
Components d'un vector
Podem multiplicar per un nombre les components d'un vector ?
Depèn. Depèn de que ens interessi del vector.
Per exemle, si hem obtingut com a vector director d'una recta el vector , per tal de no treballar amb fraccions, en comptes del vector
podem agafar el vector
, no són iguals però tenen la mateixa direcció i tant el
com el 4
són vectors directors de la recta i es pot agafar qualsevol dels dos com a vector director d'una recta.
Però si, per exemple, ens interessa el mòdul del vector, evidentment no serà el mateix agafar el vector que el 4
. Si tenen el mateix mòdul el vector
i el vector -
Atenció:
Les coordenades d'un punt mai es poden multiplicar o dividir per un nombre. Un punt té les coordenades que té i si les modifiquem obtenim altre punt. El punt (2,2,4) és un punt diferent al (1,1,2)
Equacions d'un pla
Donats
vectors directors
Punt
Equació vectorial
Equació paramètrica
Equació general o implícita
Exemple 1
Equacions del pla que passa pel punt i té vectors directors
Equació vectorial:
Equació paramètrica:
Equació implícita
la podem obtenir fent
Exemple 2
Com trobar punts d'un pla?
Trobar un punt d'un pla és molt senzill: es donen valors qualssevol a dues variables i es calcula l'altravariable. Exemple:
Volem un punt qualsevol del pla 2x-y+3z+5=0
Agafem, per exemple
Vector normal d'un pla
Donat el pla
el vector normal o vector característic del pla és .
En el llibre d'Edebé, en el tema 6 (lliurament 4) no l'utilitza. Ho utilitza i ho explica en el tema 7 (lliurament 5). Però és molt pràctic utilitzar-ho i us pot anar molt bé en molts casos per trobar fàcilment l'equació general del pla.
Aquest vector és molt important. És un vector que és perpendicular al pla. O sigui, que és perpendicular als dos vectors directors del pla.
Per tant, si sabem els vectors directors del pla, fent el producte vectorial dels plans obtenim aquest vector normal i, per tant, obtenim els coeficients del pla.
Exemple 1.
Trobeu l'equació general del pla que té vectors director normal i passa pel punt P(5,-1,0).
L'equació general del pla serà de la forma :
I si el punt (5,-1,0) ha de ser del pla, s'ha de complir:
L'equació general del pla és:
Exemple 2.
Trobeu l'equació general del pla que té vectors directors , i
i passa pel punt P(1,-1,-1).
El seu vector normal serà
Fem aquest producte vectorial:
Per tant, l'equació general del pla serà de la forma:
I trobem D per tal que passi pel punt (-1,1,-1):
L'equació general del pla és:
Observació: aquesta equació del pla també la podem trobar fent el determinant:
Feix de plans
Exercici de feix de plans.
Exemple.
Donades les rectes
Trobar el pla que conté r i és paral·lel a la recta s.
El procediment de a resolució que dóna el llibre és:
1) Considerar el feix de plans (secants) que contenen a la recta r.
2) D'aquests plans volem el que sigui paral·lel a la recta r
Aquesta condició es pot posar de diferents maneres.
a) La que fa en el llibre (aquest és l'exercici36 de la unitat 6) :
Considerar el sistema format per l'equació del pla i la recta.
Llavors, condició de paral·lelisme : recta i pla són paral·lels si el ran de la matriu de coeficients és 2 i el rang de l'ampliada és 3
b) Una condició més directe:
Condició de paral·lelisme de recta i pla:
Una recta de vector director és paral·lela a un pla de vector normal
si
és perpendicular a
, o sigui si el producte escalar d'aquest dos vectors és 0
És a dir:
 Es veu la condició en aquest petit dibuix (al vector director de la recta li ha posat
Es veu la condició en aquest petit dibuix (al vector director de la recta li ha posat )
En geometria en l'espai és molt important que us feu un petit dibuix com aquest. O que agafeu un llapis (recta) i un full (pla) ,.... i imagineu
Si ho fem amb aquesta condició.
vector normal del pla:
Vector director de la recta s:
Condició:
El pla del faig, amb és
-----------------------------------------------------------------------------------------------------------------------------------------------------
Quan expressem el feix de plans importa quin pla multipliquem per λ?
En la majoria de cassos no importa. En quins cassos importa?. Veiem un exemple.
Exemple:
Vull el pla que conté la recta i passa pel punt P(2,0,-1)
La solució seria justament el pla (ja que aquest pla passa pel punt P i, evidentment, conté a la recta)
En aquest cas, no podríem agafar el faig amb en el primer pla.
Veiem que passa si agafem:
O sigui,
ho podem posar a qualsevol dels dos plans excepte en el cas que justament el pla solució sigui un dels que defineixen la recta. En aquest cas
s'ha de posar a l'altre pla.
És per això que moltes vegades s'usen dos paràmetres diferents, un per a cada cada pla, encara que en la majoria de cassos amb un és suficient (i queda més senzill).
Bé, és una mica subtil però espero que ho entengueu.
Posicions relatives entre dos plans
Donats els plans
Coincidents

(tots els coeficients són proporcionals)
Paral·lels

(els coeficients de les variables són proporcionals però no els termes independents)
Secants

Posició relativa entre recta i pla
Donats la recta i el pla d'equacions:
O podem veure de dues maneres:
a) Considerant les matrius
Llavors:
| rang M | rang M' | |
| Recta continguda en el pla | 2 | 2 |
| Recta i pla paral·lels | 2 | 3 |
| Recta i pla secants | 3 | 3 |
b) A partir del vector director i un punt de la recta y el vector normal del pla:
recta r: vector director , punt A
pla Π: vector normal
Recta continguda en el pla

Recta i pla paral·lels

Recta i pla secants

Com trobar el punt d'intersecció d'una recta i un pla (en cas que es tallin)
Si tinc una recta i un pla que es tallen en un punt, com trobo aquest punt d'intersecció?
Hem de trobar la intersecció però aquesta intersecció la podem trobar de diferents maneres depenent de quin tipus d'equació tenim de la recta. Aconsello:
a) Si tenim l'equació implícita de la recta
recta pla
Podem resoldre el sistema d'equacions format per les equacions de la recta i el pla
Resolem aquest sistema (per exemple, per Gauss), la solució és (1,1,1)
b) Si sabem un punt i el vector director de la recta (o sigui, equació contínua o paramètrica)
recta r. punt (-1,0,4), vector director (2,1,-3)
O sigui, tindríem l'equació paramètrica de la recta:
Pla:
En aquest cas, per fer la intersecció substituïm directament la x, y, z de la recta en l'equació del pla. O sigui:
I substituint aquest valor de λ en l'equació paramètrica obtenim el punt:
Posició relativa entre dues rectes
Donades dues rectes de l'espai veiem com trobar la seva posició relativa depenent de:
- Si tenim les equacions implícites:
r:
considerarem la matriu de coeficients i la matriu ampliada del sistema format per les equacions de les dues rectes:
i mirarem els rangs de M i M'
Rectes coincidents rang M = rang M' = 2
Rectes paral·leles rang M = 2, rang M' = 3
Rectes secants rang M = rang M' = 3
Rectes que es creuen: rang M = 3, rang M' = 4
- Si sabem un punt i un vector director de cada recta.
estudiarem els vectors i els punts A i B segons els cassos
Rectes coincidents:
Rectes paral·leles:
Rectes secants:
(les dues rectes estan contingudes en un pla)
Rectes que es creuen:
(les dues rectes no estan contingudes en un pla)
MÈTRICA A L'ESPAI
.
Angles entre diferents elements de l'espai
Angle α entre dues rectes
vector director de la recta r
vector director de la recta s
Angle α entre dos plans
vector normal del pla
vector normal del pla
Angle α entre recta i pla
vector director de la recta r
vector normal del pla
Distància entre diferents elements de l'espai
Distància entre dos punts A i B
Punts i
Distància d'un punt P a una recta r
Q punt qualsevol de la recta
vector director de la recta r
Distància d'un punt P a un pla
Distància entre dues rectes r i s
a) Rectes coincidents o secants.
b) Rectes paral·leles
Es calcula la distància d'un punt qualsevol d'una recta a l'altra recta.
Sigui P punt qualsevol de la recta r
c) Rectes que es creuen
P punt de r
Q punt de s
(on indica el producte mixte)
Distància entre dos plans
a) Plans coincidents o secants.
b) Plans paral·lels
Es calcula la distància d'un punt qualsevol d'un pla a l'altre pla.
Sigui P punt qualsevol del pla
O bé:
Donats dos plans paral·lels:
Llavors:
Atenció: fixeu-vos que per poder aplicar aquesta fòrmula, els dos plans han d’estar donats amb
els mateixos coeficients de x, y, z. Això sempre serà possible si els plans són paral·lels.
Per exemple, els plans
són paral·lels, d'acord?
llavors si l'equació del pla la dividim tota entre 3, ens queda:
Distància entre recta r i pla Π
a) Recta continguda en pla o recta i pla secants
b) Recta paral·lela al pla
Es calcula la distància d'un punt qualsevol de la recta al pla.
P punt qualsevol de la recta r