Gràfica funcions
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques aplicades a les Ciències socials (autoformació IOC) |
| Llibre: | Gràfica funcions |
| Imprès per: | Usuari convidat |
| Data: | dimecres, 1 de maig 2024, 19:22 |
Descripció
Resum Lliurament 4
1. Creixement i extrems relatius
Creixement d'una funció en un punt
 |
 |
 |
|
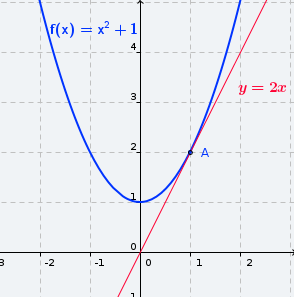
f(x) és estrictament creixent en el punt A ( en x = 1) i |
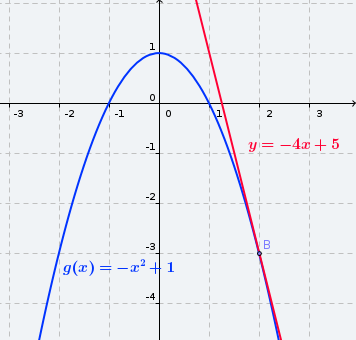
g(x) és estrictament decreixent en el punt B ( en x = 2) i |
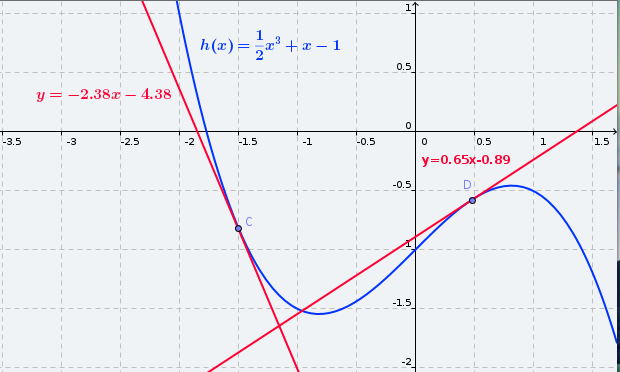
h(x) és estrictament decreixent en el punt C ( en x = -1.5) i h(x) és estrictament creixent en el punt D ( en x = 0.5) i |
Extrems relatius
Com trobar els intervals de monotonia
Per trobar els intervals de creixement i decreixement d'una funció f(x) seguim els següents passos :
1. Calcular f'(x) i resoldre l'equació f'(x) = 0 (possibles extrems).
2. Determinar els punts de discontinuïtat de la funció
3. Considerar els intervals limitats per les solucions de l'equació f'(x)=0 (trobats en el pas 1) i els punts de discontinuïtat (trobats en el pas 2).
4. Esbrinar el signe de f' en cadascun dels intervals anteriors calculant el signe de f' en un punt qualsevol d'aquest intervals. Amb el signe de f' sabrem si cada interval és de creixement o decreixement.
Com trobar els extrems relatius
Són punts on s'anul·la la derivada: f'(a)=0
(fixeu-vos que en un extrem la recta tangent sempre és horitzontal, o sigui té pendent 0)
Per saber si en x=a tal que f'(a)=0 hi ha un màxim o un mínim relatiu ho podem fer de dues maneres diferents:
a) substituïm en la derivada segona
si f''(a) > 0 => el punt (a,f(a)) és un mínim relatiu
si f''(a) < 0 => el punt (a,f(a)) és un màxim relatiu
b) (quan dibuixem funcions normalment ho farem d'aquesta manera)
si en l'interval a l'esquerra del punt la funció és creixent i en el de la dreta és decreixent => (a,f(a)) és màxim.
si en l'interval a l'esquerra del punt la funció és decreixent i en el de la dreta és creixent => (a,f(a)) és mínim.
Exemple molt senzill (sense discontinuïtats)
Estudiem el creixement, decreixement i extrems de la funció .
Procediment
-
- Calcular f ' (x). En aquest exemple f ' (x) = 2x
-
- Resoldre l'equació f ' (x)=0. Obtindrem els possibles extrems. En aquest cas seria 2x=0→ x=0. Aquí a=0
-
- Trobar els punts de discontinuïtat de la funció. La funció no té punts de discontinuïtat, ja que els polinomis són funcions contínues sempre.
-
- Ordenats de forma creixent els punts trobats, determinarem uns intervals. En el nostre cas només s'haurien format dos intervals: (-∞,0)(0,+∞)
-
- Estudiem els signe de la derivada en cada un dels intervals
En l'interval (-∞,0) podem triar per exemple x=-2. Calcularem f ' (-2). Que vol dir substituir x=-2 en f ' (x). Encara que el que importa només és el seu signe (+ o -).
f ' (-2) = 2·(-2) = -4 Per tant la funció f(x) és decreixent en tot l'interval al que pertany x = -2
En l'interval (0,+∞) podem triar per exemple x = 2. Calcularem f ' (2). Que vol dir substituir x=-2 en f ' (x). Encara que el que importa només és el seu signe (+ o -).
f ' (2) = 2·(2) = 4 Per tant la funció f(x) és creixent en tot l'interval al que pertany x=2
Resumint :
| Intervals | signe de f'(x) | f(x) és... |
| (-∞,0) | – | decreixent |
| (0,+∞) | + | creixent |
-
- Calculem l'ordenada dels punts estacionaris o extrems. Calculem la imatge de x=0, substituint x=0 en la funció f(x)→ f(0)=02=0
Com la funció a l'esquerra de x=0 és decreixent i a la dreta és creixent, necessàriament el punt x=0 és un mínim. La funció en el punt (0,0) té un mínim.
2. Extrems
Quan parlem d'extrems (màxims o mínims) en una gràfica, generalment parlem d'extrems relatius, no d'extrems absoluts.
Un mínim relatiu vol dir que és mínim en un interval.
Exemple 1

En aquesta funció tenim:
dos mínims relatius: un pròxim a x=-2 (en un entorn d'aquesta x sí és el valor mínim) i l'altre pròxim a x=1
dos màxims relatius: un pròxim a x=-1 i altre pròxima x=2
No hi ha extrems absoluts ja que la funció pren valors tan petits i tan grans com vulguem.
Exemple 2:

De fet en el punt A que posa màxim absolut, també és relatiu.
O sigui, podríem dir que aquesta funció té dos màxims relatius: A i B i un màxim absolut: A
I té un mínim relatiu en (0,0) i no té cap mínim absolut.
---------------------------------------------------------------------------------------------------------------------
El que demanem en les gràfiques (si no s'especifica) és els extrems relatius, que són els que trobem amb la condició f'(x)=0 i que són els punts on hi ha un canvi de creixement de la funció.
En l'exemple 2 veiem que en el punt B la funció passa de creixent a decreixent (sempre mirant com avança d'esquerra a dreta), encara que desprès torna a haver un canvi de decreixent a creixent (en el mínim (0,0)), i desprès en el punt A torna a canviar de creixent a decreixent (en el màxim B).
Exemple 3:
Sigui la funció .
 |
f(x) és derivable i té un mínim relatiu en x=2 Fixa-t'hi que en x=2 la recta tangent és horitzontal (pendent=0) |
Exemple 4:
Sigui la funció .
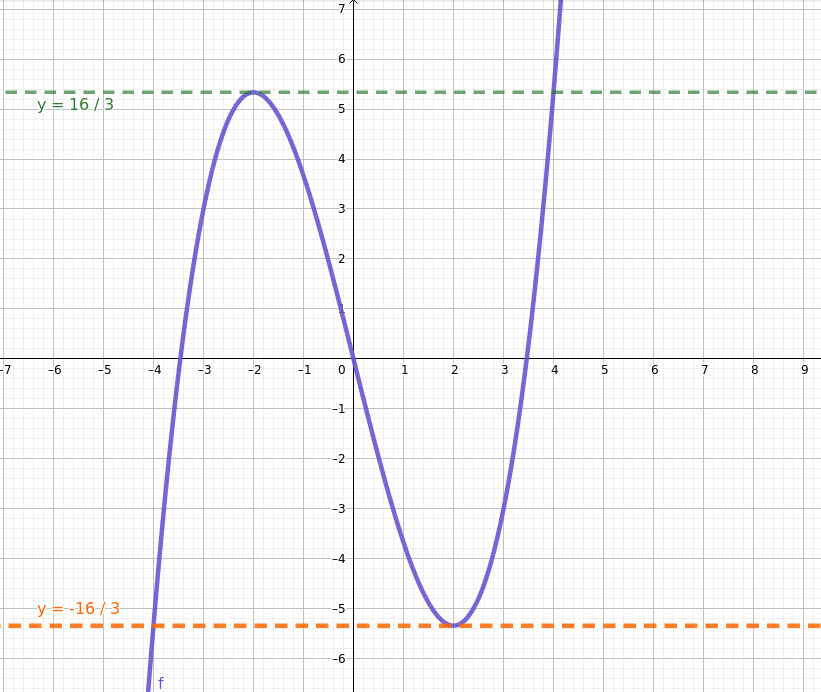 |
f(x) és derivable i té un màxim relatiu en x = -2 f(x) és derivable i té un mínim relatiu en x = 2 Fixa-t'hi que en x= -2 i en x = 2 la recta tangent és horitzontal (pendent=0) |
3. Representació gràfica
Per fer la representació gràfica d'una funció, ens limitarem a l'estudi de:
- Domini
Estudiat en la secció anterior.
- Punts de tall amb els eixos de coordenades
Talls amb l'eix x:
les "x" dels punts de tall amb l'eix x són les solucions de l'equació f(x)=0
- Asímptotes verticals i horitzontals
- Asímptotes verticals
- Asímptotes horitzontals
En la secció anterior vam veure com es trobaven.
(No estudiarem funcions amb asímptota obliqua)
- Extrems relatius
- Intervals de creixement i decreixement
- Gràfica
Aquest que hem mencionat són els conceptes més importants per estudiar una funció i fer la seva gràfica. Altres característiques són: la periodicitat, les simetries, els punts d'inflexió, la concavitat-convexitat,... però, per centra-nos en els que hem dit que són més bàsics, no els estudiarem aquí.
4. Errors i indicacions en gràfica de funcions
Comento alguns errors freqüents en els apartats per fer la gràfica de funcions que he detectat corregint la gràfica del lliurament 4 (i ara heu de fer també una en la tramesa del lliurament 5).
Domini
En general ho calculeu bé però a vegades no ho expresseu bé.
Exemple
A vegades poseu però fixeu-vos que justament aquests són els punts que no són del domini.
I a vegades poseu però això voldria dir que el domini són tots els reals excepte tots els nombres de l'interval (-1,1)
Per exemple, el domini de la funció sí és
Altre error és que quan feu l'equació només contempleu la solució positiva x=1
Talls amb els eixos
Tall amb l'eix x: f(x)=0
Per exemple, en la funció si fem
aquesta funció no talla a l'eix x.
Fixeu-vos que sempre que un quocient s'iguala a 0, ha de ser el numerador 0. Sempre:
Asímptotes verticals
En general les trobeu bé però a vegades quan feu els límits laterals feu errors de signe en l'infinit.
Atenció: si els límits laterals no es demanen explícitament, no cal calcular-los. Aquesta informació no és imprescindible per dibuixar la gràfica.
És suficient amb fer els límits globals i veure que donen infinit (i deixarem l'infinit sense concretar el signe). Farem:
I no direm l'asímptota vertical és 1 sinó que direm "l'asímptota vertical és x=1 (una asímptota no és un nombre, és una recta)
Asímptotes horitzontals
Un cop fet bé el límit, un error freqüent és dir l'asímptota horitzontal és k. Hem d'escriure: l'asímptota horitzontal és y=k
Altra error típic és quan, en el cas que sigui una funció que el seu límit a infinit sigui 0, dir que no té asímptota horitzontal. Si el límit dona 0 sí tindria i l'A.H. seria y=0
Creixement-decreixement i extrems
Aquí l'error més freqüent és en el càlcul de la derivada. Heu de repassar molt la derivada ja que si està malament ja estarà malament el creixement, els extrems i, per tant, el gràfic.
Especialment quan la funció és un quocient, molta cura amb els signes.
Exemple:
Fixeu-vos molt bé en els signes i en els parèntesis. Tots els que he posat són necessaris!. I no és una qüestió de gustos sinó de correcte o incorrecte.
Gràfica
- Comenceu marcant els talls amb els eixos que heu trobat . Un error freqüent és dibuixar la gràfica tallant als eixos en altres punts (impossible!). Dibuixeu (en línia discontinua les asímptotes)
- Tingueu en compte que la gràfica mai talla a una asímptota vertical. Sí pot tallar a una asímptota horitzontal.
- Quan dibuixeu la gràfica que s'apropa cada cop més a una asímptota, tingueu en compta que no l'arriba a tocar.
- Dibuixeu tota la gràfica, no només un tros. Vull dir que, a vegades, per exemple només la dibuixeu fins a l'asímptota vertical o,....
- Mireu que tot quadra. Especialment el creixement que heu trobat (amb la derivada) comproveu que correspon amb el de la gràfica. El creixement el mirem sempre d'esquerra a dreta, vuul dir que sempre hem de mirar la funció com avança quan les x són cada cop més grans.
Per exemple (encara que el dibuix és una mica dolent):
aquesta gràfica té:
asímptota horitzontal l'eix x y=0
asímptota vertical l'eix y x=0
la funció és decreixent fins a l'eix y decreixent en (-∞,0)
la funció és creixent a partir de l'eix y creixent en (0,+∞)
Qualsevol dubte participeu en el fòrum de Dubtes.
5. Vídeos representació gràfica
Us recomanem aquests vídeos (en castellà):
Vídeo de domini i asímptotes:
Vídeos de creixement-decreixement i extrems:
Vídeo de representación gràfica (amb tots els passos):