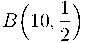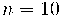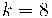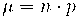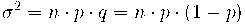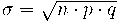Resum i dubtes més freqüents lliurament 4
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques aplicades a les C. socials I (Bloc 2) ~ gener 2020 |
| Llibre: | Resum i dubtes més freqüents lliurament 4 |
| Imprès per: | Usuari convidat |
| Data: | dimecres, 26 de juny 2024, 19:18 |
Descripció
Resum lliurament 4
1. Distribució o llei binomial
Un experiment es pot modelar amb una distribució binomial si compleix que:-
Només hi ha dos possibles successos resultants de l'experiment:
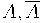 (èxit i fracàs).
(èxit i fracàs). -
Les probabilitats de cada succés
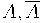 són les
mateixes en qualsevol realització de l'experiment (
són les
mateixes en qualsevol realització de l'experiment (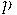 i
i 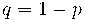 ,
respectivament). És a dir, si es tira una moneda diverses vegades, no
canvia la probabilitat d'obtenir cara.
,
respectivament). És a dir, si es tira una moneda diverses vegades, no
canvia la probabilitat d'obtenir cara. - Tota realització de l'experiment és independent de la resta.
Una variable aleatòria binomial ens donarà el nombre d'èxits en realitzar un nombre determinat d'experiments.
Per exemple, és útil per analitzar el nombre de vegades que s'obté
cara al llançar una moneda 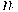 vegades.
vegades.
La distribució binomial se sol representa per 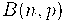 , amb:
, amb:
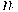 : nombre de realitzacions de l'experiment aleatori.
: nombre de realitzacions de l'experiment aleatori.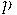 : probabilitat d'èxit en realitzar un experiment.
: probabilitat d'èxit en realitzar un experiment.
És a dir, si es vol estudiar la distribució binomial que modela
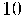 llançaments d'una moneda (en la qual la cara és igual de
probable que la creu) es té:
llançaments d'una moneda (en la qual la cara és igual de
probable que la creu) es té:
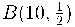
La funció de probabilitat de la distribució binomial és: 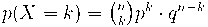
El nombre combinatori es defineix: 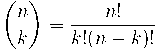
Exemple
Calculeu la probabilitat d'obtenir 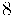 cares tirant una moneda
perfecta deu vegades.
cares tirant una moneda
perfecta deu vegades.
probabilitat de cada èxit i de cada fracàs: 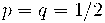
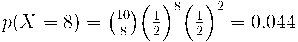 el que es pot interpretar com el producte de les combinacions possibles
de
el que es pot interpretar com el producte de les combinacions possibles
de 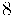 cares i
cares i 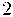 creus, per la probabilitat de treure
creus, per la probabilitat de treure 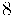 cares, per la probabilitat de treure
cares, per la probabilitat de treure 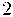 creus.
creus.
2. Distribució o llei normal
La variable aleatòria contínua segueix una distribució normal
segueix una distribució normal  , és a dir de mitjana
, és a dir de mitjana  i desviació típica
i desviació típica  , si compleix que:
, si compleix que:- Pot prendre qualsevol valor real:

- La funció densitat de probabilitat (fpd o pdf de l'anglès) segueix una corba gaussiana:

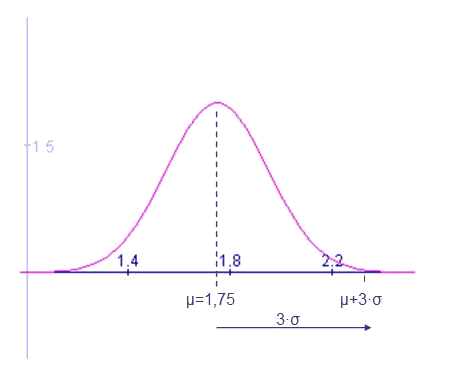
La distribució normal estàndard
La distribució normal estàndard és la que té mitjana  i desviació típica
i desviació típica  ,
, 
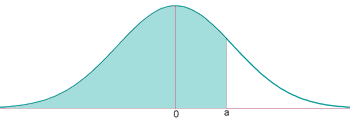
En la següent gràfica veiem la seva representació:
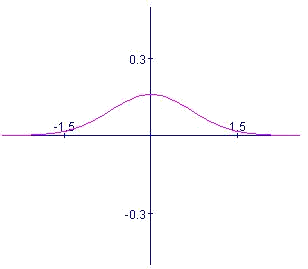
A continuació, es pot veure la taula corresponent als valors de la funció distribució de probabilitat, és a dir: 
La primera posició de la taula indica la probabilitat que el resultat de l'experiment d'un valor inferior a zero (la mitjana), i es pot observar que aquesta probabilitat és  . La taula mostra que la probabilitat d'un resultat menor que un determinat valor
. La taula mostra que la probabilitat d'un resultat menor que un determinat valor  creix a mesura que creix
creix a mesura que creix  .
.
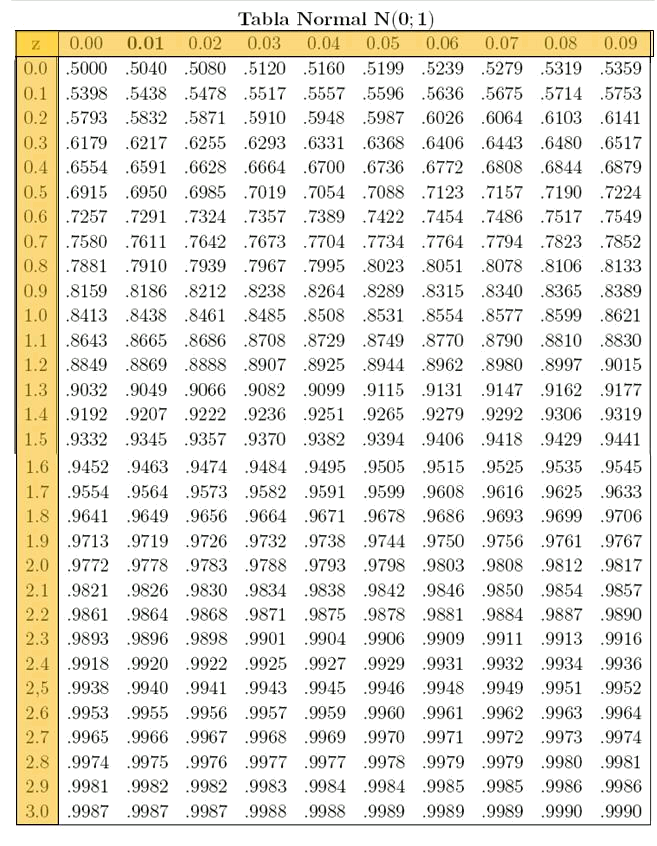
Per interpretar la taula s'ha de veure que la fila indica la unitat i la desena de  , mentre que la columna indica el segon decimal (la centèsima). És a dir, a la primera casella de la primera fila es veu la probabilitat
, mentre que la columna indica el segon decimal (la centèsima). És a dir, a la primera casella de la primera fila es veu la probabilitat 
mentre que en la darrera casella de la primera fila es veu: 
Es pot observar que la taula només dóna les probabilitats per a valors positius de  . Per als valors de
. Per als valors de  s'utilitzarà la simetria.
s'utilitzarà la simetria.
Val a dir que a partir de  (
( vegades la desviació típica) la probabilitat és molt propera a 1
vegades la desviació típica) la probabilitat és molt propera a 1  . Per simetria per a valors menors a
. Per simetria per a valors menors a  , la probabilitat serà pràcticament nul·la.
, la probabilitat serà pràcticament nul·la.
Exemple
Trobar la probabilitat que una variable aleatòria  que es modela com
que es modela com  tingui un valor menor que
tingui un valor menor que  .
.
3. Nombres combinatoris. Com es calculen.
En la distribució binomial apareixen els nombres combinatoris.
Quan escrivim no volem dir 15 dividit per 3 , si no que volem dir el nombre combinatori 15 sobre 3.
Com es calcula el nombre combinatori:

on el símbol d'admiració vol dir el següent : 6!= 6·5·4·3·2·1
Les calculadores fan aquests nombres combinatoris. Estan en una tecla nCr
Si vols calcular cliques 15 (shift) nCr 3 = i obtens : 455
Aquests nombres el que compten són les diferents combinacions
4. Problema resolt de llei binomial
|
Un agent d'assegurances ven pòlisses a cinc persones de la mateixa edat i amb bona salut. Segons les taules actuals, la probabilitat de que una persona en aquestes condicions visqui 30 anys o més es 2/3. Calculeu la probabilitat de que passats 30 anys, visquin: a) les 5 persones b) al menys tres persones c) Exactament dues persones |
Soluciones:
a) les 5 persones
B(5, 2/3) p = 2/3 q = 1/3

b) al menys tres persones
![]()

c) Exactament dues persones

5. Problema resolt de llei normal (I)
|
La mitjana dels pesos de 500 estudiants d'una escola és de 70 kg de pes i la desviació típica o estàndard és de 3kg. Suposant que el pes és una variable Normal, calculeu quants estudiants pesen: a) Entre 60 kg i 75 kg b) Més de 90 kg c) Menys de 64 kg |
a) Entre 60 kg i 75 kg
![]()
![]()
![]()
Aquesta és la probabilitat, és a dir el 95,21 % dels estudiants estan entre 60kg i 75 kg
Ara cal aplicar aquest % sobre 500 estudiants
0,9521 · 500 = 476
Resposta 476 alumnes estan entre 60 kg i 75 kg.
b) Més de 90 kg
![]()
=1-P(Z<6,67) = 1-1=0
El valor 6,67 no surt a la taula
El 0% pesa més de 90 kg
"0" alumnes pesen més de 90 kg
c) Menys de 64 kg
![]()
= 1- 0,9772 = 0,0228
El 2,28 % dels alumnes pesen menys de 64 kg.
0,0228 · 500 = 11,4
11 alumnes pesen menys de 64 kg
6. Problema resolt de llei normal (II)
|
Suposem que el pes dels atletes de marató segueix una distribució normal N(62, 3,4).
a) Calcula la probabilitat que un atleta pesi més de 65 kg. b) El 70 % dels atletes no supera un pes. Quin? |
a) Calcula la probabilitat que un atleta pesi més de 65 kg.
X= N(62, 3,4)
Per poder utilitzar la taula de la N(0,1) cal tipificar la variable X
Cal buscar en la taula de la Normal (0,1) el nombre 0,88.
b) El 70 % dels atletes no supera un pes. Quin?
70% → 0,70 →
Hem de buscar dins de la taula de la Normal (0,1) el valor més aproximat a 0,70:

Hem triat 0,7019 que dóna un valor de 0,53. Per tant, .
Aïllem "" →
.
7. Procediment abreujat problemes de Normal
Pautes per realitzar un problema sobre distribució Normal.
1r. Comprovar que en l'enunciat del problema es parla de distribució Normal, identificar la mitjana aritmètica (μ) i la desviació (σ). X=N(μ,σ)2n. Tipificar la variable.
3r. Buscar en la taula de la Normal (0,1) el valor oportú. A vegades no és fàcil saber quin és el valor oportú. Veiem alguns exemples. La taula dóna els valors P(Z<a) amb "a" un valor positiu:
3.1 Si es vol calcular P(Z<2,58) . Basta buscar 2,58 en la taula i obtindrem: P(Z< 2,58) = 0,9951.
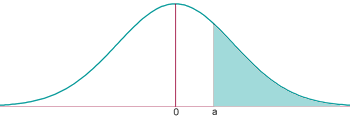
3.2 Si es vol calcular P(Z>2,58). Aquesta probabilitat no la dóna la taula, i per tant cal anar en compte. P(Z>2,58) = 1- (Z<2,58) = 1- 0,9951 = 0,0049.
3.3 Si es vol calcular P(Z<–2,58). Aquesta probabilitat no la dóna la taula, per què és un nombre negatiu i per tant cal anar en compte. P(Z<–2,58) = 1- (Z<2,58) = 1- 0,9951 = 0,0049.
3.4 Si es vol calcular P(Z>–2,58)=P(Z<2,58) = 0,9951.
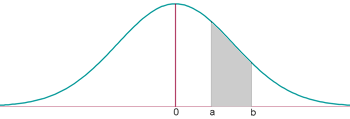
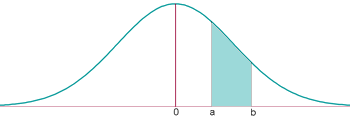
3.5 Si es vol calcular P(a<Z<b) = P(Z<b)- P(Z<a).
Resumint la taula dóna una probabilitat P(Z<a) amb a positiu:
P(Z<a) la dóna la taula, buscant el valor "a"

P(Z>a) = 1 - (el que diu la taula en "a")

P(Z<–a)= 1 - (el que diu la taula en "a")

P(Z>–a) = el que diu la taula en "a"
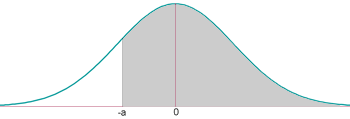
P(a<Z<b) = P(Z<b)- P(Z<a) = (el que diu la taula en "b") - (el que diu la taula en "a")