Resum Geometria i Programació lineal
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques aplicades a les Ciències socials (autoformació IOC) |
| Llibre: | Resum Geometria i Programació lineal |
| Imprès per: | Usuari convidat |
| Data: | divendres, 3 de maig 2024, 15:54 |
Descripció
Programació lineal
Taula de continguts
- 1. Punts i vectors
- 2. Equacions de la recta
- 3. Qüestions bàsiques de geometria
- 4. Exemples trobar equació recta
- 5. Gràfica d'una recta
- 6. Equació de la recta que passa per dos punts
- 7. Inequacions lineals amb una incògnita
- 8. Inequacions lineals amb dues incògnites
- 9. Sistemes d'inequacions
- 10. Problema d'optimització
1. Punts i vectors
Punts en un sistema de coordenades cartesianes.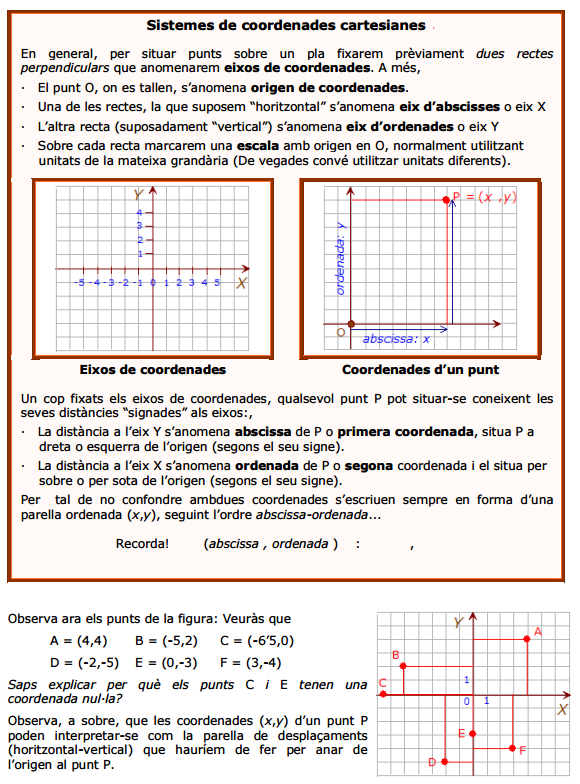
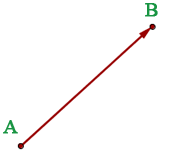 Elements d'un vector:
Elements d'un vector:
Direcció: direcció de la recta que el conté.
Sentit: el que va de l'origen a l'extrem.
Mòdul: longitud del segment AB, es representa per
Components d'un vector
Si les coordenades dels punts A i B són:
Les components del vector són les coordenades de l'extrem menys les de l'origen.
Exemple
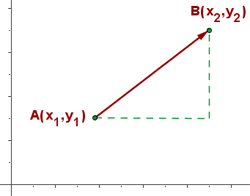 Si les coordenades dels punts són:
Si les coordenades dels punts són:
Les components del vector són:
2. Equacions de la recta
Rectes en el pla
Una recta ve determinada per:
- Dos punts: donats dos punts, existeix una única recta que passa per ells
o bé per:
- Un punt i una direcció: la direcció pot venir donada pel vector director, per l'angle d'inclinació o bé per el pendent de la recta.


Equacions de la recta
Una equació de la recta és una igualtat que verifiquen tots els punts de la recta i només aquests.
Hi ha diferents tipus d'equació de la recta. Depenent de les dades que tinguem, serà més pràctic utilitzar una o altra.
Equació general o implícita
Un vector director de la recta és
si el v.d. és , llavors l'equació de la recta és
Equació explícita
Si en l'equació general aïllem la variable y obtenim:
el coeficient de la x és el pendent de la recta
D'aquesta manera obtenim l'equació:
on m és el pendent de la recta
Observació:
hem dit que si el v.d. és , llavors l'equació de la recta és
aïllant la y tenim:
Per tant,
O sigui, que si el v.d. és
Equació contínua
Si tenim el v.d. i un punt
de la recta, l'equació contínua de la recta és:
Aquest tipus d'equació és molt pràctic quan sabem vector director i punt.
Si voleu més informació o exemples, podeu veure els webs:
Equacions de la recta (on diu "ecuaciones de la recta")
Tipus d'equacions de la recta (a la dreta teniu l'índex per veure els diferents tipus d'equació)
Hem dit que una recta amb vector director té pendent
El vector director ens dóna la direcció de la recta
El pendent de la recta ens dóna la "inclinació" de la recta.
Està clar que la relació entre vector director i pendent és molt estreta.
Si la recta passa pels punts , el seu v.d és el vector que va d'un punt a l'altre
 vector director:
vector director:
Pendent:
Si
el v.d. és
i el pendent és
(i , si recordeu de trigonometria, això és la tangent de l'angle α )
3. Qüestions bàsiques de geometria
Qüestió 1
Com sabem si un punt és d'una recta ax+by+c=0 ?
Exemple:
Donada la recta
El punt (5,1) és de la recta r?
substituïm els valors x=5, y=1 en l'equació de la recta:
3·5-2·1+1= 0 ?
15-2+1=0 ? NO El punt (5,1) no és de la recta r
El punt (3,5) és de la recta r?
substituïm els valors x=3, y=5 en l'equació de la recta:
3·3-2·5+1= 0 ?
9-10+1=0 ? SI El punt (3,5) sí és de la recta r
Questió 2
Donats , quines són les components del vector
?
i el vector ?
són iguals els vectors i el
?
No, no són iguals ja que , tenen sentit oposat
Sí tenen la mateixa direcció. Per tant, com a vector director de la recta que passa per A i B podem agafar tant el vector com el
(ja que tenen la mateixa direcció)
Qüestió 3
Quin és el vector director de la recta ?
Recordem que el v.d. de la recta és
Per tant,
el v.d de és
i el pendent m de la recta ?
o bé aïllem y:
o també sabent que el vector director és
Qüestió 4
Quin és el vector director de la recta ?
Recordem que el v.d. de la recta és
Per tant,
el v.d de és
Observació:
Com a vector director de la recta també podem agafar el vector:
ja que té la mateixa direcció que el
, encara que sentit oposat
o el que té la mateixa direcció i sentit que el
, però el mòdul (la longitud) és la meitat.
4. Exemples trobar equació recta
Exemple 1 Equació general
Trobar la recta que passa pel punt i té vector director
Recordem: El vector director de la recta ax+by+c=0 és (-b,a)
o dit d'altra manera:
v.d. , l'equació general:
Per tant, si el vector director és l'equació de la recta serà de la forma:
I trobem c perquè la recta passi per , que vol dir que ha de complir l'equació:
Per tant l'equació de la recta és:
També podem posar tota l'equació canviada de signe:
Exemple 2 Equació contínua
Trobar la recta que passa pel punt i té vector director
Recordem: vector director , punt
Equació contínua:
Observació: d'aquesta equació podem passar fàcilment a l'equació general de l'exemple 1:
Exemple 3 Equació explícita
Trobar la recta que passa pel punt i té vector director
Recordem: v.d. és
Equació explícita:
Per tant, v.d
L'equació implícita serà de la forma:
Trobem la n sabent que el punt és de la recta:
Per tant:
Exemple 4
Trobar la recta que passa pel punt i té pendent 5.
En aquest cas l'equació més pràctica serà l'explícita:
Com que directament ens donen la dada del pendent, m=5, tenim:
Passa pel punt
Equació de la recta:
o també podem expressar l'equació general que, simplement, és igualant a zero:
5. Gràfica d'una recta
Per dibuixar una recta, primer de tot heu de tenir clar com representem un punt P(x,y). En aquest enllaç podeu veure la representació de punts en uns eixos de coordenades: Punts i vectors
Com trobem punts d'una recta?
Volem obtenir punts (x,y), o sigui, parells de valors de x i y que satisfacin l'equació de la recta.
Una recta té infinits punts. Podem donar el valor qualsevol a una de les variable i trobar el valor de l'altre variable per tal es satisfaci l'equació.
Exemple 1
Trobem punts de la recta
Podem donar valors a la variable x i trobar el valor de y :
Si Punt
Si
Punt
O podem donar valors a la variable y i trobar el valor de x :
Si
Punt
Exemple 2
recta
Per exemple, podem trobar el punt amb x=0,
Substituïm aquest valor x=o en l'equació:
Per tant tenim el punt
De fet amb trobar dos punts tenim suficient per dibuixar la recta
En la taula següent trobem diversos punts de cada recta, donant diferents valors a la x i trobant la y corresponent:
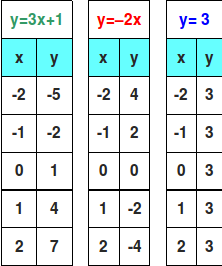
Amb aquest punts de cada recta, dibuixem les rectes:
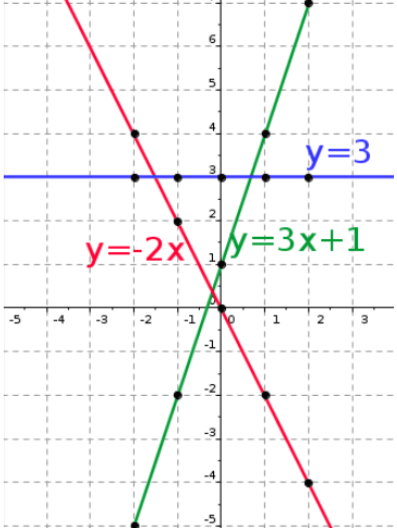
i en aquest enllaç podeu veure com, donat un sistema de dues equacions amb dues incògnites, podem trobar la solució gràficament dibuixant les dues rectes. El punt solució del sistema és el punt de tall (o punt intersecció) de les dues rectes:
6. Equació de la recta que passa per dos punts
Veurem diferents maneres de trobar l'equació de la recta que passa per dos punts:
Exemple 1
Trobeu l'equació de la recta que passa pels punts A(2,1) i B(-3,5)
Volem trobar l'equació del tipus
O sigui, hem de trobar m i n
Que els punts siguin de la recta vol dir que han de verificar l'equació:
Ara tenim plantejat un sistema d'equacions on les incògnites són m i n
Ho fem per reducció, simplement canviem el signe de la 2a equació i sumem les dues equacions:
(m és el pendent de la recta)
I substituint aquest valor en la primera equació 1=2m+n obtenim n:
Per tant, l'equació de la recta és:
Observacions:
- El pendent de la recta és m. Aquesta recta té pendent -4/5
- A partir d'aquesta equació podem obtenir l'equació general de la recta:
Exemple 2
Trobeu l'equació de la recta que passa pels punts A(2,1) i B(-3,5)
Un vector director de la recta serà
Ara amb el v.d i el punt
ja podem expressar l'equació continua:
O si volem l'equació general:
Observacions:
- Fixeu-vos que aïllant la variable y d'aquesta última equació, obtenim l'equació explícita trobada en l'exemple 1.
- Per expressar l'equació explícita hem agafat el punt A, també podríem haver agafat el punt B (el resultat seria el mateix).
7. Inequacions lineals amb una incògnita
Definició.
Una inequació és una desigualtat entre dues expressions algebraiques, anomenades membre de la inequació.
Els valors de les incògnites que fan que sigui certa la desigualtat són les solucions de la inequació.
Diem que dues inequacions són equivalents si tenen el mateix conjunt solució.
Una inequació lineal amb una incògnita és una equació equivalent a
Propietats.
- Si sumem o restem una mateixa expressió polinòmica al dos membre de la inequació, obtenim una inequació equivalent.
- Si multipliquem o dividim per un nombre positiu els dos membres d'una inequació, obtenim una inequació equivalent.
Exemple:
- Si multipliquem o dividim per un nombre negatiu els dos membres d'una inequació, per obtenir una inequació equivalent hem d'invertit el sentit de la desigualtat.
Exemple:
Solucions.
El conjunt de solucions el podem expressar en forma d'interval o fent la representació gràfica.
Exemple:
8. Inequacions lineals amb dues incògnites
És una expressió equivalent a
amb qualsevol de les desigualtats <, ≤, >, ≥
Solucions
La solució és un semiplà. Hem de representar gràficament aquest semiplà.
Exemple:
Dibuixem la recta
Per dibuixar-la trobem dos punts qualssevol de la recta:
Aquesta recta divideix al pla en dos semiplans. La recta és la frontera d'aquests semiplans.
Els punts de la recta verifiquen y=-2x+3
Els punts d'un semiplà verifiquen y<-2x+3 i els de l'altre semiplà verifiquen y>-2x+3
Per saber quin semiplà correspon a cada inequació agafem un punt de cada semiplà i veiem quina desigualtat compleix.
Veiem, per exemple, que el punt (-3,1) compleix y<-2x+3. Tots els punts que es troben en el mateix semiplà que el (-3,1)
compliran y<-2x+3
Tots els punts de l'altre semiplà compliran la desigualtat y>-2x+3. Per exemple, ho podem veure amb el punt
És molt pràctic mirant-ho amb el punt (0,0):
Substituïm el (0,0) en la inequació i mirem si la compleix o no :
En aquest cas veiem que el (0,0) compleix 2·0+0 < 3, per tant compleix la inequació.
Per tant, el semiplà solució és el semiplà que conté al punt (0,0). En el dibuix ho hem indicat en groc.
Quan la desigualtat sigui estricta vol dir que la solució no inclou als punts de la recta i, llavors, la dibuixarem amb un traç continu.
Indiquem en groc el semiplà solució de les corresponents inequacions.
Casos particulars.
Si estem treballant amb dues variables però tenim desigualtats amb una única variable, veiem gràficament el semiplà solució:
Exemples:
x < 2 x 2 x > 2 x
2
y < 3 y 3 y > 3 y
2
9. Sistemes d'inequacions
Un sistema d'inequacions lineal amb dues variables és de la forma
(amb qualsevol de les desigualtats
Ho resolem gràficament.
Dibuixem, en uns mateixos eixos de coordenades, el semiplà solució de cada inequació
La solució del sistema serà la regió intersecció dels dos plans.
Observeu que pot ser que un sistema d'inequacions no tingui solució. Això passarà quan els dos semiplans no tinguin cap punt en comú.
9.1. Exemple
Exemple
Hem de dibuixar les dues rectes 2x+3y=1 i x-y=3 en uns mateixos eixos de coordenades.
Per dibuixar-les trobem dos punts de cada recta.
Recta
Recta
Ratllem en verd la solució de la inequació
Podem veure que el punt (0,0) SÏ compleix la inequació, ja que
Per tant el semiplà solució és en el qual es troba el (0,0)
Ratllem en blau la solució de la inequació
Podem veure que el punt (0,0) NO compleix la inequació, ja que
Per tant el semiplà solució és en el qual no es troba el (0,0)
La regió solució és la regió ratllada
tant de blau com de vermell.
veiem que en aquest cas és una regió oberta.
9.2. Problema
Passos a seguir per resoldre un problema mitjançant un sistema d'inequacions:
- Llegir atentament l'enunciat.
- Escollir les incògnites.
- Traduir cada condició (o restricció) del problema en una inequació, obtenint un sistema d'inequacions.
- Resoldre el sistema d'inequacions indicant la regió solució.
- Obtenir les solucions i comprovar-les.
Exemple
Disposem d'un màxim de 55€ i hem de comprar al menys 5 bolígrafs i 5 carpetes. Cada bolígraf costa 3€ i cada carpeta 5€.
Troba totes les opcions de compra.
Solució
bolígràfs: x
carpetes: y
Hem de dibuixar, en uns mateixos eixos de coordenades, les tres rectes 3x+5y=55, x=5 (recta vertical) i y=5 (recta horitzontal) i
veure amb quin semiplà ens quedem.
La intersecció d'aquest semiplans és la regió solució. En aquest cas és un triangle.
els vèrtexs del qual són els punts d'intersecció de les rectes
dos a dos.
Les solucions de x, y seran els punts (x,y) que es troben dins del triangle solució.
En general, per indicar la solució del sistema serà suficient amb marcar la regió solució en el dibuix.
--------------------------------------------------------------------------------------------------------------------------------------------------------------
En aquest cas hem d'afinar més si tenim en compte que, com que parlem de nombre de bolígrafs (x) i nombre de capetes (y),
les solucions han de ser nombres naturals:
Trobem els vèrtex de la regió solució. Són els punts d'intersecció de les rectes
dos a dos.
En aquest cas els vèrtex A i C no són solució ja que la desigualtat és estricta (els punts de la recta 3x+5y=55 no són solució.
Els punts amb coordenades enteres que estan en ela regió solució són:
(5,5), (6,5), (7,5), (8,5), (9,5) 5 carpetes i entre 5 i 9 bolígrafs
(5,6), (6,6), (7,6) 6 carpetes i entre 5 i 7 bolígrafs
(5,7), (6,7) 7 carpetes i 5 o 6 bolígrafs
(5,8) 8 carpetes i 5 bolígrafs.
10. Problema d'optimització
Resoldre un problema de programació lineal consisteix a optimitzar (maximitzar o minimitzar) una funció lineal, anomenada funció objectiu, subjecta a unes restriccions expressades mitjançant un sistema d'inequacions lineal.
Passos a seguir:
- Llegir atentament l'enunciat i escollir les incògnites.
- Resoldre el sistema d'inequacions format per les restriccions. A la regió solució del sistema l'anomenem regió factible.
- Obtenir els vèrtexs de la regió factible.
- Calcular el valor de la funció objectiu en cadascun dels vèrtexs per tal de determinar en quin pren el valor màxim o mínim.
10.1. Exemple 1
Una empresa fabrica ordinadors portàtils i de sobretaula i ven tots els que fabrica. L'empresa té capacitat per a fabricar 3000 ordinadors. Per qüestions de mercat, el nombre d'ordinadors de sobretaula no pot ser inferior a la meitat del nombre de portàtils, però tampoc pot superar el nombre de portàtils. L'empresa guanya 100 € per cada ordinador de sobretaula, i un 20% més en la venda de cada portàtil.
a) Escriu el sistema d'inequacions que satisfà les restriccions del problema.
Anomenarem x al nombre d'ordinadors de sobretaula, i y al de portàtils.
Restriccions:
- L'empresa té capacitat per a fabricar 3000 ordinadors
- El nombre d'ordinadors de sobretaula no pot ser inferior a la meitat del nombre de portàtils.
- El nombre d'ordinadors no pot superar el nombre de portàtils.
Sistema d'inequacions:
b) dibuixa la regió factible i troba els seus vèrtex.
Dibuixem les rectes
Cadascuna d'aquestes rectes divideix al pla en dos semiplans. Hem de mirar quins semiplans compleixen les inequacions.
Podem veure que el (0,0) compleix la inequació. Per tant és el semiplà on es troba el (0,0)
En aquest cas com que el (0,0) és de la recta, agafem altre punt. Per exemple, el (1000,0).
Veiem que Per tant, és el semiplà on es troba el punt (1000,0)
Agafem, per exemple, el (1000,0).
Com que 1000 > 0, no compleix la inequació. El pla solució no és el pla on es troba el punt (100,0)
En aquest cas la regió factible és l'interior d'aquest triangle. Trobem els seus vèrtexs.
I l'altre vèrtex serà òbviament el
c) Quants ordinadors de cada classe ha de fabricar per tal de maximitzar els seus beneficis?
La funció objectiu és:
En aquest cas volem un màxim d'aquesta funció.
Avaluem aquesta funció en cadascun dels vèrtexs:
Per tant el màxim benefici s'obté fabricant 1000 ordinadors portàtils i 2000 de sobretaula.
10.2. Exemple 2
Una empresa de confecció produeix abrics i vestits. Per a la confecció de cada abric es necessiten 6 hores de treball i 2m de roba i per a la confecció d'un vestit 3 hores de treball i 4 m de roba. cada abric produeix un benefici de 80 € i cada vestit un benefici de 50 €. L'empresa disposa de 2850 hores de treball i de 1700 m de roba.
a) Escriu el sistema d'inequacions que satisfà les restriccions del problema.
| hores de treball | metres de roba | benefici | |
| abrics | 6 | 2 | 80 |
| vestits | 3 | 4 | 50 |
| 2850 | 1700 |
Anomenarem x al nombre d'abrics, i y al de vestits.
Sistema d'inequacions:
b) Dibuixa la regió factible i troba els seus vèrtex.
Dibuixem les rectes
Cadascuna d'aquestes rectes divideix al pla en dos semiplans. Hem de mirar quins semiplans compleixen les inequacions.
Podem veure que el (0,0) compleix la inequació. Per tant és el semiplà on es troba el (0,0)
Podem veure que el (0,0) compleix la inequació. Per tant és el semiplà on es troba el (0,0)
En aquest cas la regió factible és l'interior d'aquest polígon. Trobem els seus vèrtexs.
Veient el dibuix els altres vèrtexs són obvis. Per tant tenim que els vèrtex de la regió factible són:
A(0,425), B(350,250), C(475,0), D(0,0)
c) Quants abrics i vestits cal fabricar per obtenir el benefici màxim?
La funció objectiu és:
En aquest cas volem un màxim d'aquesta funció.
Avaluem aquesta funció en cadascun dels vèrtexs:
Per tant el màxim benefici s'obté fabricant 350 abrics i 250 vestits.
10.3. Exemple 3
Exemple en vídeoVídeo
Problema de programació lineal