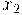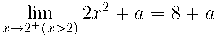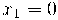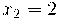Resum conceptes bàsics del lliurament 2

lloc:	Cursos IOC - Batxillerat
Curs:	Matemàtiques II (Bloc 2) ~ gener 2020
Llibre:	Resum conceptes bàsics del lliurament 2

Imprès per:	Usuari convidat
Data:	divendres, 10 de maig 2024, 06:54

Descripció

Resum

Taula de continguts

1. Continuïtat
2. Funcions amb valor absolut
3. Teorema de Bolzano
- 3.1. Aplicació T. Bolzano en la resolució d'equacions

Continuïtat

Una funció és contínua si la poden dibuixar sense aixecar el llapis de paper. Els punts on sigui necessari aixecar el llapis de paper serà discontínua.

Si de la funció es coneix la gràfica és fàcil respondre a les preguntes: És una funció contínua? I si és discontínua, en quins punts és discontínua? Quins tipus de discontinuïtat té la funció?

Però en la majoria de les ocasions volem saber si la funció és contínua sense tenir la seva representació gràfica. És més, necessitem saber la continuïtat de la funció per tal de trobar de manera més fàcil la seva gràfica.

És per això que estudiarem la continuïtat de la funció o bé a partir de la seva gràfica o bé a partir de l'equació i amb l'ajut dels límits.

Procediment per estudiar la continuïtat d'una funció coneixent la seva expressió algebraica

S'ha de calcular el domini de la funció, per detectar possibles punts de discontinuïtat.
S'han de calcular límits laterals en aquest punts.
Cal calcular les imatges d'aquests punts si existeixen.
Si la funció es definida a trossos, cal estudiar també els límits laterals i la imatge dels punts de transició (on es passa d'un tros a l'altra). I esbrinar si compleix aquesta igualtat de límits que determina si una funció és contínua:

$límit quan x fletxa dreta obre parèntesis x subíndex 0 tanca parèntesis elevat a menys de espai espai f parèntesi esquerre x parèntesi dret espai igual límit quan x fletxa dreta obre parèntesis x subíndex 0 tanca parèntesis elevat a més de espai espai f parèntesi esquerre x parèntesi dret igual f parèntesi esquerre x subíndex 0 parèntesi dret$

Observeu aquests exemples:

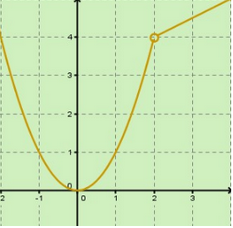
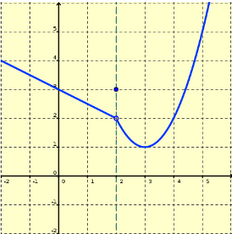
Funció contínua	Funció discontínua en x₀amb discontinuïtat evitable
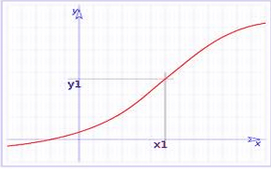
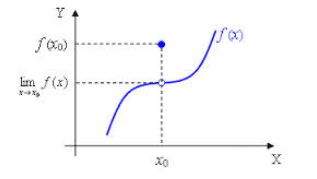
Aquesta funció és contínua ja que: $límit quan x fletxa dreta obre parèntesis x subíndex 0 tanca parèntesis elevat a menys de espai espai f parèntesi esquerre x parèntesi dret espai igual límit quan x fletxa dreta obre parèntesis x subíndex 0 tanca parèntesis elevat a més de espai espai f parèntesi esquerre x parèntesi dret igual f parèntesi esquerre x subíndex 0 parèntesi dret$	Aquesta funció no és contínua. Ell punt (x₀, f(x₀)) fa que sigui discontínua. Els límits laterals (les dues branques) coincideixen. 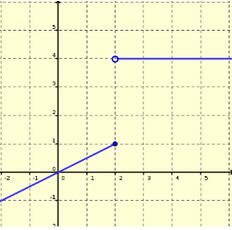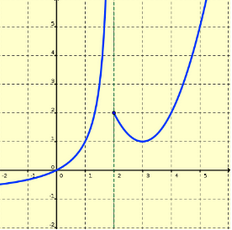$límit quan x fletxa dreta obre parèntesis x subíndex 0 tanca parèntesis elevat a menys de espai espai f parèntesi esquerre x parèntesi dret espai igual límit quan x fletxa dreta obre parèntesis x subíndex 0 tanca parèntesis elevat a més de espai espai f parèntesi esquerre x parèntesi dret no igual f parèntesi esquerre x subíndex 0 parèntesi dret$
Funció discontínua en x₀amb discontinuïtat de salt	Funció discontínua en x₀amb discontinuïtat asimptòtica
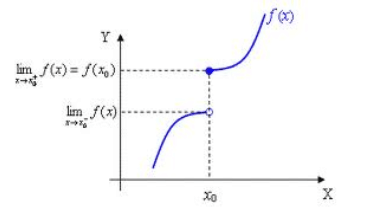
Aquesta funció no és contínua. Les dues branques no es troben. Això fa que la funció sigui discontínua. I ell punt (x₀, f(x₀)) està situat sobre una de les dues branques. Hi ha un salt. 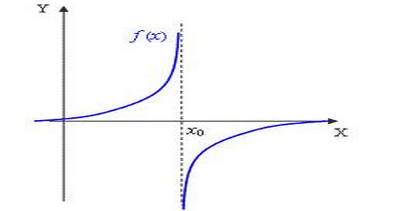$límit quan x fletxa dreta obre parèntesis x subíndex 0 tanca parèntesis elevat a menys de espai espai f parèntesi esquerre x parèntesi dret espai no igual límit quan x fletxa dreta obre parèntesis x subíndex 0 tanca parèntesis elevat a més de espai espai f parèntesi esquerre x parèntesi dret igual f parèntesi esquerre x subíndex 0 parèntesi dret$	Aquesta funció no és contínua. Ell punt (x₀, f(x₀)) no existeix, no és del domini de la funció. Les dues branques no es troben i s'enfilen cap al ∞. Tot això fa que sigui discontínua. $límit quan x fletxa dreta obre parèntesis x subíndex 0 tanca parèntesis elevat a menys de espai espai f parèntesi esquerre x parèntesi dret espai no igual límit quan x fletxa dreta obre parèntesis x subíndex 0 tanca parèntesis elevat a més de espai espai f parèntesi esquerre x parèntesi dret$ i a més $f parèntesi esquerre x subíndex 0 parèntesi dret espai n o espai e x i s t e i x$

Com distingir entre els diferents tipus de discontinuïtat

Una funció és contínua en x=a si es compleix: $espai espai espai espai pila l i m amb x fletxa dreta a elevat a menys a sota f parèntesi esquerre x parèntesi dret espai igual pila l i m amb x fletxa dreta a elevat a més a sota f parèntesi esquerre x parèntesi dret espai igual f parèntesi esquerre a parèntesi dret$

Si hi ha discontinuïtat i cal classificar-la, heu de conèixer que hi ha tres tipus de discontinuïtat:

evitable
de salt finit i
de salt infinit o asimptòtica.

Depèn de la/ les condicions que no es compleixin tindrem un tipus de discontinuïtat o un altre

Cas 1: Discontinuïtat evitable en x=a

Per tal que la discontinuïtat sigui evitable, s'ha de donar la situació següent: els límits laterals en x=a coincideixen (límit per l'esquerra i per la dreta ) i són un nombre finit (no infinit) però no coincideix amb la imatge f(a) ( ja sigui perquè no n’hi ha o bé perquè és un nombre diferent).

Exemple 1:

obre taula atributs alineació columna right fin atributs fila cel·la obre taula atributs alineació columna right fin atributs fila cel·la límit quan x fletxa dreta 2 elevat a més de espai f parèntesi esquerre x parèntesi dret igual 4 fi cel·la fila cel·la límit quan x fletxa dreta 2 elevat a menys de espai f parèntesi esquerre x parèntesi dret igual 4 fi cel·la fi taula tanca claus fletxa dreta límit quan x fletxa dreta 2 de espai f parèntesi esquerre x parèntesi dret igual 4 P e r ò espai f parèntesi esquerre 2 parèntesi dret espai n o espai e x i s t e i x fi cel·la fila blank fi taula tanca claus fletxa doble dreta f parèntesi esquerre x parèntesi dret espai t é espai u n a espai d i s c o n t i n u ï t a t espai e v i t a b l e espai e n espai x igual 2

Exemple 2:

obre taula atributs alineació columna right fin atributs fila cel·la obre taula atributs alineació columna right fin atributs fila cel·la límit quan x fletxa dreta 2 elevat a més de espai f parèntesi esquerre x parèntesi dret igual 2 fi cel·la fila cel·la límit quan x fletxa dreta 2 elevat a menys de espai f parèntesi esquerre x parèntesi dret igual 2 fi cel·la fi taula tanca claus fletxa dreta límit quan x fletxa dreta 2 de espai f parèntesi esquerre x parèntesi dret igual 2 f parèntesi esquerre 2 parèntesi dret igual 3 espai p e r ò espai n o espai c o i n c i d e i x espai fi cel·la fila cel·la a m b espai e l espai l í m i t espai espai espai espai espai espai fi cel·la fi taula tanca claus fletxa doble dreta f parèntesi esquerre x parèntesi dret espai t é espai u n a espai d i s c o n t i n u ï t a t espai e v i t a b l e espai e n espai x igual 2

Cas 2: Discontinuïtat de salt finit en x=a

El límits laterals són diferents. I a més són finits.

La imatge f(a) pot existir o no (no importa)

Exemple 3:

obre taula atributs alineació columna right fin atributs fila cel·la obre taula atributs alineació columna right fin atributs fila cel·la límit quan x fletxa dreta 2 elevat a més de espai f parèntesi esquerre x parèntesi dret igual 4 fi cel·la fila cel·la límit quan x fletxa dreta 2 elevat a menys de espai f parèntesi esquerre x parèntesi dret igual 1 fi cel·la fi taula tanca claus fletxa dreta límit quan x fletxa dreta 2 de espai f parèntesi esquerre x parèntesi dret igual no existeix f parèntesi esquerre 2 parèntesi dret igual 1 espai fi cel·la fila blank fi taula tanca claus fletxa doble dreta f parèntesi esquerre x parèntesi dret espai t é espai u n a espai d i s c o n t i n u ï t a t espai d e espai s a l t espai f i n i t espai e n espai x igual 2

Cas 3: Discontinuïtat asimptòtica o de salt infinit en x=a

Un dels límits laterals en x=a o els dos dóna ∞

La imatge f(a) pot existir o no (no importa)

Exemple 4:

$obre taula atributs alineació columna right fin atributs fila cel·la obre taula atributs alineació columna right fin atributs fila cel·la límit quan x fletxa dreta 2 elevat a més de espai f parèntesi esquerre x parèntesi dret igual 2 fi cel·la fila cel·la límit quan x fletxa dreta 2 elevat a menys de espai f parèntesi esquerre x parèntesi dret igual més infinit fi cel·la fi taula tanca claus fletxa dreta límit quan x fletxa dreta 2 de espai f parèntesi esquerre x parèntesi dret igual no existeix f parèntesi esquerre 2 parèntesi dret igual 2 espai fi cel·la fila blank fi taula tanca claus fletxa doble dreta f parèntesi esquerre x parèntesi dret espai t é espai u n a espai d i s c o n t i n u ï t a t espai a s i m p t ò t i c a espai e n espai x igual 2$

Exemple d'estudi de funcions

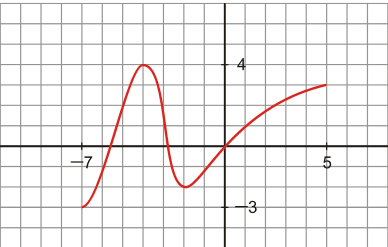
Aquí es mostren unes gràfiques, a partir de les quals, us demanem observar les següents característiques: domini, punts de talls, límits i continuïtat.

Gràfica 1

Aquesta gràfica comença en x=-7 i finalitza en x=5

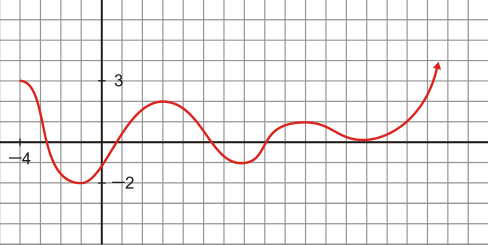
Gràfica 2

Aquesta gràfica comença en x=-4 i segueix indefinidament

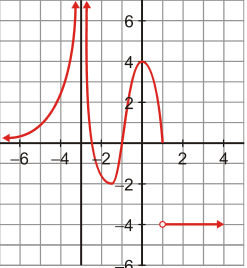
Gràfica 3

Aquesta gràfica segueix indefinidament per les dues puntes

Gràfica 4

Aquesta gràfica segueix indefinidament per les dues puntes

Resposta:


Característiques	Gràfica 1	Gràfica 2	Gràfica 3	Gràfica 4
Dom f(x)	Interval [-7,5]	[-4,+∞]	Tots els reals = R	R - {-3}
Punts tall eix X	(0,0) (-2.9 , 0) (5.5 , 0)	(13,0) (8,0) (5.5, 0) (1.5, 0) (-2.5, 0)	(2,0) (4,0) (-3,0)	(1,0) (-1,0) (-2.5 , 0)
Punts tall Eix Y	(0,0)	(0,-1)	(0,3)	(0,4)
$límit quan x fletxa dreta més infinit de f parèntesi esquerre x parèntesi dret$	= no existeix	$igual més infinit$	$igual menys infinit$	= 4
$límit quan x fletxa dreta menys infinit de f parèntesi esquerre x parèntesi dret$	= no existeix	= no existeix	$igual més infinit$	= 0
Altres límits				$límit quan x fletxa dreta menys 3 elevat a menys de f parèntesi esquerre x parèntesi dret igual més infinit$ $límit quan x fletxa dreta 1 elevat a menys de f parèntesi esquerre x parèntesi dret igual 0$ $límit quan x fletxa dreta 1 elevat a més de f parèntesi esquerre x parèntesi dret igual menys 4$ $límit quan x fletxa dreta menys 3 elevat a més de f parèntesi esquerre x parèntesi dret igual més infinit$
És contínua?	Sí	Sí	Sí	És discontínua en: x=-3 i en x=1

Exercici:
Donada la funció : $f parèntesi esquerre x parèntesi dret igual fracció numerador 2 x al quadrat més k x entre denominador x més 2 k fi fracció espai$ es demana:
Explicar raonadament quin valor ha de tenir el paràmetre k per tal que la funció sigui discontínua en x=6.

Classifiqueu aquesta discontinuïtat.

Solució:

Una funció és contínua en un punt (x=6) si es compleix aquesta igualtat: $límit quan x fletxa dreta 6 elevat a més de f parèntesi esquerre x parèntesi dret espai igual límit quan x fletxa dreta 6 elevat a menys de f parèntesi esquerre x parèntesi dret espai igual f parèntesi esquerre 6 parèntesi dret$

Aquesta no és una funció a trossos per tant basta calcular el límit quan x tendeix a 6.

$límit quan x fletxa dreta 6 de f parèntesi esquerre x parèntesi dret espai igual límit quan x fletxa dreta 6 de fracció numerador 2 x al quadrat més k x entre denominador x més 2 k fi fracció espai igual parèntesi esquerre c a l espai s u b s t i t u i r espai x espai p e r espai 6 parèntesi dret igual límit quan x fletxa dreta 6 de fracció numerador 2 per 6 al quadrat més k parèntesi esquerre 6 parèntesi dret entre denominador 6 més 2 k fi fracció igual fracció numerador 72 més 6 k entre denominador 6 més 2 k fi fracció igual fracció numerador ratllat diagonal cap amunt 2 per parèntesi esquerre 36 més 3 k parèntesi dret entre denominador ratllat diagonal cap amunt 2 per parèntesi esquerre 3 més k parèntesi dret fi fracció igual fracció numerador 36 més 3 k entre denominador 3 més k fi fracció$

Es vol que la funció sigui discontínua, o sigui es vol que aquest límit no sigui un nombre real.

Això passarà quan el denominador sigui zero. Per tant : $3 més k igual 0 espai espai espai espai fletxa doble dreta envoltori caixa k igual menys 3 fi envoltori$

Observeu que :

$límit quan x fletxa dreta 6 de f parèntesi esquerre x parèntesi dret espai igual límit quan x fletxa dreta 6 de fracció numerador 2 x al quadrat més k x entre denominador x més 2 k fi fracció espai igual fracció numerador 36 més 3 k entre denominador 3 més k fi fracció igual parèntesi esquerre a r a espai s u b s t i t u i m espai k igual menys 3 parèntesi dret igual fracció numerador 36 més 3 parèntesi esquerre menys 3 parèntesi dret entre denominador 3 més parèntesi esquerre menys 3 parèntesi dret fi fracció igual fracció 27 entre 0 igual infinit$

La funció en x=6 té una discontinuïtat asimptòtica, si k= - 3

Funció definida a trossos.

Donada la funció

$f (x) = \{\begin{cases} - 3 x + 1 s i x < 1 \\ x^{2} + a s i x \geq 1 \end{cases}$

a) Calculeu el domini de la funció $f (x)$

b) Calculeu el valor d' a per tal que la funció sigui contínua en x = 1

c) Calculeu $\lim_{x \to + \infty} f (x)$ prenent com a valor de "a" el que has obtingut en l'apartat anterior.

d) Calculeu $\lim_{x \to - \infty} f (x)$ prenent com a valor de "a" el que has obtingut en l'apartat anterior.

e) Calculeu les imatges de x=-1 , de x=1 i de x=3 i preneu el valor de "a" el que has obtingut en l'apartat b)

f) Feu la gràfica de la funció

Resposta :

a) Domini de la funció f(x).

Cal estudiar cada una de les dues parts de la funció per separat i també els punts de transició d'una funció a l'altra.


Part I	Part II	Punt de transició entre la part I i la II
$g (x) = - 3 x + 1$	$p (x) = x ² + a$	En el punt x=1 hi ha imatge. $f (1) = 1^{2} + a = a + 1$
g(x) és funció polinòmica de 1r grau. És, per tant, una recta. És contínua.	p(x) és una funció polinòmica de 2n grau. És una paràbola. És contínua.
Dom g(x) = Reals	Dom p(x) = Reals	x =1 és del domini

Per tant Dom f(x) = Reals

b) Estudia la continuïtat de la funció en x= 1 i en cas que la funció sigui discontínua, digues de quin tipus.

Recordeu que una funció és contínua en un punt x₀ si es compleix :_{$\lim_{x \to {x_{0}}^{+}} f (x) = \lim_{x \to {x_{0}}^{-}} f (x) = f (x_{0})$}

Estudiarem el comportament de la funció en x=1

$\lim_{x \to 1^{-}} f (x) = \lim_{x \to 1^{-}} (- 3 x + 1) = - 3 (1) + 1 = - 2$	A l'esquerra de 1 li correspon la funció de la part I
$\lim_{x \to 1^{+}} f (x) = \lim_{x \to 1^{+}} (x ² + a) = (1 ²) + a = 1 + a$	A a dreta de 1 li correspon la funció de la part II
$f (1) = 1 + a$	Tal i com està definida la funció, la imatge de x=1 es busca en la funció de la part II

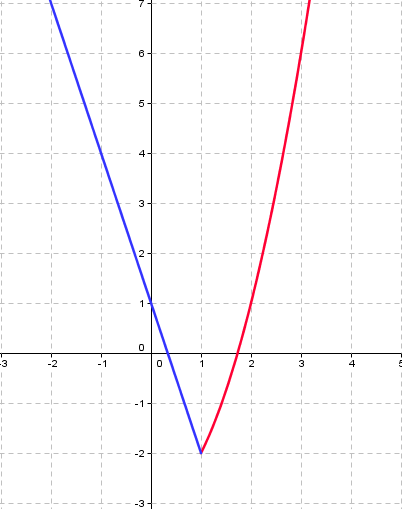
Per tal que els tres valors coincideixen, cal que 1+a =-2 → a= -3

Per tant la funció serà contínua per a=-3 i discontínua si a≠-3

c) Calcula

$\lim_{x \to + \infty} f (x) = \lim_{x \to + \infty} (x ² + a) = + \infty$

d) Calcula

$\lim_{x \to - \infty} f (x) = \lim_{x \to - \infty} (- 3 x + 1) = + \infty$

e) Calculeu les imatges de x=-1 de x=1 i de x=3 i "a" pren el valor obtingut en l'apartat b

$f (- 1) = - 3 (- 1) + 1 = 4$
$f (1) = 1^{2} + a = 1 - 3 = - 2$
$f (3) = 3^{2} - 3 = 6$

f) Gràfica

Donada la funció f(x) definida a trossos: $f parèntesi esquerre x parèntesi dret espai igual espai obre claus taula atributs alineació columna left fin atributs fila cel·la 4 dividit per x espai espai espai espai espai espai espai espai espai espai espai espai espai espai s i espai espai espai espai espai espai x menor o igual que 2 fi cel·la fila cel·la 2 x al quadrat espai més negreta espai bold italic a espai espai espai espai espai espai espai s i espai espai espai espai x major que 2 fi cel·la fi taula tanca$ , trobeu: a) El domini de la funció. b) El valor d' a per tal que la funció sigui contínua en x= 2. c) Els punts on és discontínua la funció f (x) i classifiqueu les discontinuïtats. Si obriu el programa geogebra en línia que teniu disponible a l'aula podeu representar aquesta funció i comprovar els resultats que heu obtingut. Per introduir la fórmula de la funció en el geogebra cal escriure en la línia d'entrada la funció en aquest format Funció[4/x,-∞,2] i doneu a la tecla "intro". Us sortirà la primera part de la funció Ara introduïu en la línia d'entrada Funció[2x^2+a,1,∞] i doneu a la tecla "intro". I us sortirà la segona part de la funció. Però cal posar el valor concret de "a" que heu trobat al resoldre l'apartat b). Aquest apartat no és imprescindible, però us ajudarà a interpretar els límits. </td> </tr> </tbody> </table> Aquesta és una funció definida a trossos. a) Domini de la funció f (x) Hi ha algun punt on no es pugui calcular la seva imatge? La funció està formada per dues parts. Caldrà estudiar cada una de les funció i també què passa en el punt de transició d'una funció a l'altra. <table class="generaltable" id="yui_3_17_2_1_1527787602083_2784" style="width: 90%;"> <caption></caption> <thead id="yui_3_17_2_1_1527787602083_3057"> <tr style="background-color:#EEEEEE" id="yui_3_17_2_1_1527787602083_2871"> <th scope="col" id="yui_3_17_2_1_1527787602083_2879">Part I</th> <th scope="col" id="yui_3_17_2_1_1527787602083_2883">Part II</th> <th scope="col">Punt de transició entre la part I i la II</th> </tr> </thead> <tbody id="yui_3_17_2_1_1527787602083_2783"> <tr id="yui_3_17_2_1_1527787602083_2866"> <td id="yui_3_17_2_1_1527787602083_2880"> $h parèntesi esquerre x parèntesi dret espai igual fracció 4 entre x$ </td> <td id="yui_3_17_2_1_1527787602083_2884"> $g parèntesi esquerre x parèntesi dret igual 2 x al quadrat més a$ </td> <td>x=2</td> </tr> <tr id="yui_3_17_2_1_1527787602083_2782"> <td id="yui_3_17_2_1_1527787602083_2881"> En la funció h(x) no que es pot calcular la imatge de x=0. Per trobar les "x" que no pertanyen al domini, s'ha d'igualar a zero l denominador $fletxa doble dreta$ x=0 I s'obté que el punt que no és del domini és x1=0. </td> <td id="yui_3_17_2_1_1527787602083_2832">g(x) és una funció polinòmica de 2n grau. És una paràbola. No cal fer res. El domini són tots els reals.</td><td id="yui_3_17_2_1_1527787602083_2781">Per obtenir la imatge de x=2, hem triat la primera funció, ja que: La funció $h parèntesi esquerre x parèntesi dret espai igual espai fracció 4 entre x$ correspon a l'interval x≤2 (inclou x=2) La funció $g parèntesi esquerre x parèntesi dret espai igual 2 x al quadrat més a$ correspon a l'interval dels valors x>2 (no inclou x=2) </td> </tr> <tr id="yui_3_17_2_1_1527787602083_2875"> <td id="yui_3_17_2_1_1527787602083_2882"> Dom(h) = tots els reals menys el zero = R - {0}

Domg(x)=Reals

x=2 és del domini

Per tant Dom f(x) = Reals - {0}

Els dos valors x₁= 0 ix₂ =2 obtinguts en aquest apartat, són els valors on caldrà estudiar els límits i on es comprovarà que hi ha discontinuïtat.

b) Continuïtat de la funció

Recordeu que una funció f(x) és contínua en $x=a$ , i a és del domini de f(x) i $\small {\lim }\limits_{x \to a^-} = {\lim }\limits_{x \to a^+}= f(a)$

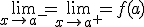
Totes les funcions presenten discontinuïtats per totes aquelles 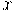$x$ que no pertanyen al domini ( les funcions definides a trossos també poden presentar discontinuïtats als punts de separació entre els trossos).

- - - Càlcul de límits laterals en x₁=0 punt que no és del domini

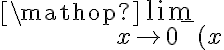$\mathop {\lim }\limits_{x \to 0^ - (x$	-∞
$\mathop {\lim }\limits_{x \to 0^+ (x>0)} \frac{{4}}{{x}} = \frac{{4}}{{0^+}} =$	+∞

La imatge en aquest punt no existeix, donat que no és un punt del domini

En x₁=0 el límits laterals obtinguts han donat infinit, per tant la funció 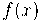$f(x)$ presenta una discontinuïtat asimptòtica.

- - - Càlcul de límits laterals i la imatge en x₂=2 punt de transició

$\mathop {\lim} \limits_{x \to 2^- (x$	Per calcular aquest límit cal substituir el valor $x_2$ en la funció
$\mathop {\lim} \limits_{x \to 2^+ (x>2)}{2x^2+a}=8+a$	Per calcular aquest límit cal substituir el valor $x_2$ en la funció
Imatge f(2)=4/2 = 2	Per calcular la imatge del punt, cal substituir el valor $x_2$ en la funció

Aquests tres valors haurien de coincidir per ta que la funció sigui contínua.

Hem de trobar el valor de "a" per tal que els tres valors siguin iguals: 2= 8+a → a = - 6

c) Punts de discontinuïtat

Ho hem esbrinat en l'apartat anterior

$x_1=0$ el límits laterals obtinguts han donat infinit, per tant la funció

$f(x)$ presenta una discontinuïtat asimptòtica

La funció

$f(x)$ és contínua en

$x_2=2$ si a= -6

Estudia la continuïtat de la funció:

f parèntesi esquerre x parèntesi dret igual obre claus taula atributs alineació columna left left fin atributs fila cel·la menys x fi cel·la cel·la espai espai espai espai s i espai x menor que menys 1 fi cel·la fila cel·la x menys 1 fi cel·la cel·la espai espai espai espai s i espai menys 1 menor o igual que x menor que 3 fi cel·la fila cel·la menys x al quadrat més 2 x més 5 fi cel·la cel·la espai espai espai espai s i espai x major o igual que 3 fi cel·la fi taula tanca

Resposta :

a) Domini de la funció f(x).

Cal estudiar cada una de les tres parts de la funció per separat i també els punts de transició d'una funció a l'altra.


Part I	Part II	Part III	Punt de transició entre la part I i la II	Punt de transició entre la part II i la III
g(x)=-x	p(x)=x-1	h(x)=-x²+2x+5	x=-1	x=3
g(x) és funció polinòmica de 1r grau És una recta No cal fer res	p(x) és una funció polinòmica de 1r grau És una recta No cal fer res	h(x) és una funció polinòmica de 2n grau És una recta No cal fer res
Dom g(x) = Reals	Dom p(x) = Reals	Dom h(x) = Reals	x=-1 és del domini	x=3 és del domini

Per tant Dom f(x) = Reals

b) Estudiarem la continuïtat de la funció en x= -1 i en x=3 i classificarem la discontinuïtat, cas que n'hi hagi:

Recordeu que una funció és contínua en un punt x_{0 :}

Estudiarem el comportament de la funció en x=-1

$pila l i m amb x fletxa dreta parèntesi esquerre menys 1 parèntesi dret elevat a menys a sota f parèntesi esquerre x parèntesi dret espai igual pila l i m amb x fletxa dreta parèntesi esquerre menys 1 parèntesi dret elevat a menys a sota menys x espai igual espai menys parèntesi esquerre menys 1 parèntesi dret espai igual espai 1 espai$	A l'esquerra de -1 li correspon la funció de la part I
$pila l i m amb x fletxa dreta parèntesi esquerre menys 1 parèntesi dret elevat a més a sota f parèntesi esquerre x parèntesi dret espai igual pila l i m amb x fletxa dreta parèntesi esquerre menys 1 parèntesi dret elevat a més a sota x menys 1 espai igual espai parèntesi esquerre menys 1 parèntesi dret menys 1 espai igual espai menys 2$	A a dreta de -1 li correspon la funció de la part II
	x=-1 per tany a la part II

Veiem que aquest tres valors NO coincideixen per tant la funció és discontínua en x=-1 i és una discontinuïtat de SALT FINIT

c) Estudiarem la continuïtat de la funció en x=3 i la classificarem, cas que n'hi hagi

$pila l i m amb x fletxa dreta parèntesi esquerre 3 parèntesi dret elevat a menys a sota f parèntesi esquerre x parèntesi dret espai igual pila l i m amb x fletxa dreta parèntesi esquerre 3 parèntesi dret elevat a menys a sota x menys 1 espai igual espai 3 menys 1 espai igual espai 2$	A l'esquerra de 3 li correspon la funció de la part II
$pila l i m amb x fletxa dreta parèntesi esquerre 3 parèntesi dret elevat a més a sota f parèntesi esquerre x parèntesi dret espai igual pila l i m amb x fletxa dreta parèntesi esquerre 3 parèntesi dret elevat a més a sota menys x al quadrat més 2 x més 5 espai igual menys espai parèntesi esquerre 3 parèntesi dret al quadrat més 2 parèntesi esquerre 3 parèntesi dret més 5 espai igual espai 2$	A a dreta de 3 li correspon la funció de la part III
	x=3 per tany a la part III

Veiem que aquest tres valors SI coincideixen per tant la funció és contínua en x=3

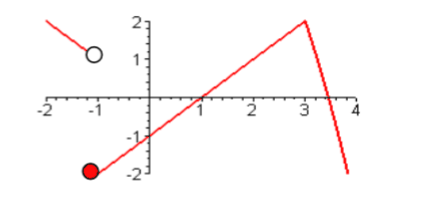
Com puc expressar una funció amb valors absoluts com una funció a trossos?

Per poder trobar l'expressió d'una funció amb valors absoluts com una funció a trossos i sense valors absoluts cal seguir bàsicament els següents passos:

1. Esbrinar per a cada valor absolt quan l'expressió de dins és positiva i quan és negativa

2. Els valors on l'expressió doni positiva podem treure el valor absolut doncs queda igual

3. Els valors on l'expressió doni negativa podem treure el valor absolut canviat el signe de tota aquesta expressió

4. Escriure la funció a trossos equivalent amb el nombre de trossos que haguem trobat.

Exemple1

Sigui la funció $f parèntesi esquerre x parèntesi dret igual obre barra vertical 6 menys 2 x tanca barra vertical$

Anem a seguir les passes descrites abans:

1r pas:

$6 menys 2 x major o igual que 0 espai espai fletxa dreta 6 major o igual que 2 x espai fletxa dreta fracció 6 entre 2 major o igual que x espai fletxa dreta 3 major o igual que x p e r espai tan t espai s i espai x pertany parèntesi esquerre menys infinit coma 3 claudàtor dret espai l l a v o r s espai 6 menys 2 x espai major o igual que 0 espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai espai s i espai x pertany parèntesi esquerre 3 coma més infinit parèntesi dret espai l l a v o r s espai 6 menys 2 x espai menor que 0$

2n pas:

$s i espai x pertany parèntesi esquerre menys infinit coma 3 claudàtor dret espai l l a v o r s espai 6 menys 2 x espai major o igual que 0 espai espai i espai p e r espai tan t espai l a espai f u n c i ó espai q u e d a espai i g u a l espai espai f parèntesi esquerre x parèntesi dret igual 6 menys 2 x$

3r pas:

$s i espai x pertany parèntesi esquerre 3 coma més infinit parèntesi dret espai l l a v o r s espai 6 menys 2 x espai menor que 0 espai espai i espai p e r espai tan t espai l a espai f u n c i ó espai q u e d a espai c a n v i a d a espai d e espai s i g n e espai espai f parèntesi esquerre x parèntesi dret igual menys parèntesi esquerre 6 menys 2 x parèntesi dret igual menys 6 més 2 x$

4t pas:

$f parèntesi esquerre x parèntesi dret igual obre claus taula atributs alineació columna left fin atributs fila cel·la 6 menys 2 x espai espai espai s i espai x menor o igual que 3 fi cel·la fila cel·la menys 6 més 2 x espai espai espai s i espai x major que 3 fi cel·la fi taula tanca$

Exemple2

Sigui la funció $f parèntesi esquerre x parèntesi dret igual 3 espai obre barra vertical x al quadrat menys 4 tanca barra vertical$

Observem en primer lloc que entre el 3 i el valor absolut hi ha un producte (implícit) $f parèntesi esquerre x parèntesi dret igual 3 per espai obre barra vertical x al quadrat menys 4 tanca barra vertical$

Anem a seguir les passes descrites abans:

1r pas:

$x al quadrat menys 4 major o igual que 0 fletxa dreta x al quadrat igual 4 fletxa dreta espai espai x igual més-menys 2 A r a espai c o l per l o q u e m espai e l s espai n o m b r e s espai menys 2 espai i espai 2 espai i espai v e i e m espai q u e espai l a espai r e c t a espai r e a l espai q u e d a espai d i v i d i d a espai e n espai t r e s espai t r o s s o s.$

Haurem de mirar per cada tros si x²-4 és positiu o negatiu. Per això agafem un valor dins de cada tros i substituïm

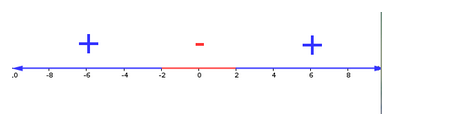
2n pas:

$s i espai x pertany parèntesi esquerre menys infinit coma menys 2 claudàtor dret espai l l a v o r s espai x al quadrat menys 4 espai major o igual que 0 espai espai i espai p e r espai tan t espai l a espai f u n c i ó espai q u e d a espai i g u a l espai espai f parèntesi esquerre x parèntesi dret igual 3 per parèntesi esquerre x al quadrat menys 4 parèntesi dret igual 3 x al quadrat menys 12 s i espai x pertany claudàtor esquerre 2 coma més infinit parèntesi dret espai l l a v o r s espai x al quadrat menys 4 espai major o igual que 0 espai espai i espai p e r espai tan t espai l a espai f u n c i ó espai q u e d a espai i g u a l espai espai f parèntesi esquerre x parèntesi dret igual 3 per parèntesi esquerre x al quadrat menys 4 parèntesi dret igual 3 x al quadrat menys 12$

3r pas:

$s i espai x pertany parèntesi esquerre menys 2 coma 2 parèntesi dret espai espai l l a v o r s espai x al quadrat menys 4 espai menor que 0 espai espai i espai p e r espai tan t espai l a espai p a r t espai d e l espai v a l o r espai a b s o l u t espai q u e d a espai c a n v i a t espai d e espai s i g n e espai espai f parèntesi esquerre x parèntesi dret igual 3 per parèntesi esquerre menys parèntesi esquerre x al quadrat menys 4 parèntesi dret parèntesi dret igual menys 3 x al quadrat més 12$

4t pas:

$f parèntesi esquerre x parèntesi dret igual obre claus taula fila cel·la 3 x al quadrat menys 12 espai espai espai s i espai espai x menor o igual que menys 2 fi cel·la fila cel·la menys 3 x al quadrat més 12 espai espai espai s i espai espai menys 2 menor que x menor que 2 fi cel·la fila cel·la 3 x al quadrat menys 12 espai espai espai s i espai espai x major o igual que 2 espai espai espai fi cel·la fi taula tanca$

Perquè no puc aplicar Bolzano si la funció no és contínua en l'interval tancat?

El teorema de Bolzano diu que si una funció f (x) és contínua en un interval tancat [a,b] i en els extrems d'aquests pren valors de diferent signe $obre parèntesis f parèntesi esquerre a parèntesi dret per f parèntesi esquerre b parèntesi dret menor que 0 tanca parèntesis$ , aleshores hi ha almenys un valor $c pertany parèntesi esquerre a coma b parèntesi dret$ tal que $f parèntesi esquerre c parèntesi dret igual 0$

Dit de forma més planera, si una funció contínua, té una part de la seva gràfica per sota de l'eix horitzontal i una part per sobre, vol dir que en algun punt talla a l'eix, i per tant hi ha algun punt de la funció tindrà y=0, o sigui hi haurà un zero de la funció.

Exemple 1:

Ara considerem la funció f(x) que té per gràfica

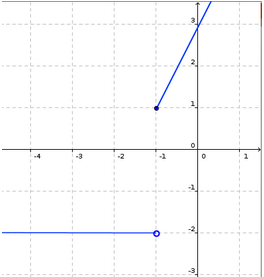
Veiem que $f parèntesi esquerre 0 parèntesi dret per f parèntesi esquerre menys 2 parèntesi dret igual 3 per parèntesi esquerre menys 2 parèntesi dret menor que 0$ però en canvi no existeix cap arrel en l'interval (-2,0).

Això és degut a que la funció no és contínua en [-2,0] doncs en x = -1 presenta una discontinuïtat de salt.

Per tant al no complir-se una de les condicions o hipòtesis del teorema no podem garantir que existeixi un zero de la funció entre -2 i 0

Exemple 2:

Ara considerem la funció f(x) que té per gràfica

Veiem que $f parèntesi esquerre 1 parèntesi dret per f parèntesi esquerre 3 parèntesi dret igual parèntesi esquerre menys 1 parèntesi dret per 2 menor que 0$ però en canvi no existeix cap arrel en l'interval (1,3).

Això és degut a que la funció no és contínua en [1,3] doncs en x = 1 presenta una discontinuïtat de salt.

Per tant al no complir-se una de les condicions o hipòtesis del teorema no podem garantir que existeixi un zero de la funció entre 1 i 3

Però observeu en la mateixa funció anterior que si fem l'estudi en l'interval [-2,1]. Veiem que:

f(-2)=2 => positiva. O sigui la funció en x=-2 està per sobre de l'eix X (del nivell horitzontal)

f(1)=-1=> negativa. O sigui la funció en x=1 està per sota de l'eix X (del nivell horitzontal)

Per tant f(-2) · f(1) <0

La funció és contínua en l'interval [-2,1]

Podem concloure (pel Teorema de Bolzano) que en algun punt de l'interval [-2,1] es complirà f(c)=0. I si veiem el dibuix és cert que en f(0)=0

Justifiqueu que la funció polinòmica f(x) = x³ + x + 1 té un zero comprés entre −1 y 0.

O sigui que aquesta equació x³ + x + 1=0 té una solució, el valor de la qual està entre -1 i 0

Aproximeu aquest valor a 1 decimal.

Resposta:

Buscar el zero d'una funció f(x) és equivalent a resoldre l'equació f(x)=0 i trobar la solució.

A vegades trobar una solució d'una equació és difícil, per això en ocasions es pot usar el T. de Bolzano, i tractar de "cercar-la"

De l'enunciat es pot pensar que la solució està en [-1,0], i per tant serà aproximadament : x= -1 o bé x≈-0,9 o bé x≈-0,8 o bé x≈-0,7 .... o bé x≈-0,1 o bé x=0

Apliquem el T. de Bolzano en l'interval [-1,0]

$estil mida 12px espai espai espai obre taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la f parèntesi esquerre x parèntesi dret espai é s espai u n a espai f u n c i ó espai p o l i n ò m i c a espai i espai p e r espai t a n t espai é s espai c o n t i n u a espai e n espai e l espai i n t e r v a l espai claudàtor esquerre menys 1 coma espai 0 claudàtor dret fi cel·la fila cel·la f parèntesi esquerre menys 1 parèntesi dret espai igual espai parèntesi esquerre menys 1 parèntesi dret al cub espai més espai parèntesi esquerre menys 1 parèntesi dret espai més espai 1 espai igual espai menys 1 espai menor que espai 0 fi cel·la fila cel·la f parèntesi esquerre 0 parèntesi dret espai igual espai 0 espai més espai 0 espai més espai 1 major que 0 fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula tanca claus fletxa doble dreta P e l espai T. B o l z a n o espai e x i s t e i x espai u n espai v a l o r espai " c " espai q u e espai espai c espai pertany espai parèntesi esquerre menys 1 coma espai 0 parèntesi dret espai t a l espai q u e dos punts espai f parèntesi esquerre c parèntesi dret espai igual espai 0 fi estil$

Per tant segur que hi ha (al menys) un valor que és solució de l'equació i que aquest valor és x≈-0,9 o bé x≈-0,8 o bé x≈-0,7 .... o bé x≈-0,1

Per afinar més i saber el primer decimal de la solució hem de fer el punt mig de l'interval [−1, -0.5]

$estil mida 12px espai espai espai obre taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la f parèntesi esquerre x parèntesi dret espai é s espai u n a espai f u n c i ó espai p o l i n ò m i c a espai i espai p e r espai t a n t espai é s espai c o n t i n u a espai e n espai e l espai i n t e r v a l espai claudàtor esquerre menys 1 coma espai menys 0.5 claudàtor dret fi cel·la fila cel·la f parèntesi esquerre menys 1 parèntesi dret espai igual espai parèntesi esquerre menys 1 parèntesi dret al cub espai més espai parèntesi esquerre menys 1 parèntesi dret espai més espai 1 espai igual espai menys 1 espai menor que espai 0 fi cel·la fila cel·la f parèntesi esquerre menys 0.5 parèntesi dret espai igual espai parèntesi esquerre menys 0.5 parèntesi dret al cub espai més espai parèntesi esquerre menys 0.5 parèntesi dret espai més espai 1 igual 0.375 major que 0 fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula tanca claus fletxa doble dreta P e l espai T. B o l z a n o espai e x i s t e i x espai u n espai v a l o r espai " c " espai q u e espai espai c espai pertany espai parèntesi esquerre menys 1 coma menys 0.5 parèntesi dret espai t a l espai q u e dos punts espai f parèntesi esquerre c parèntesi dret espai igual espai 0 fi estil$

Per tant x≈-0,9 o bé x≈-0,8 o bé x≈-0,7 .... o bé x≈-0,5

Seguim, tornem a dividir l'interval en dues parts i provarem en l'interval [−1, -0.8]. I si no funciona buscarem en l'interval [−0,8, -0.5]

$estil mida 12px espai espai espai obre taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la f parèntesi esquerre x parèntesi dret espai é s espai u n a espai f u n c i ó espai p o l i n ò m i c a espai i espai p e r espai t a n t espai é s espai c o n t i n u a espai e n espai e l espai i n t e r v a l espai claudàtor esquerre menys 1 coma espai menys 0.8 claudàtor dret fi cel·la fila cel·la f parèntesi esquerre menys 1 parèntesi dret espai igual espai parèntesi esquerre menys 1 parèntesi dret al cub espai més espai parèntesi esquerre menys 1 parèntesi dret espai més espai 1 espai igual espai menys 1 espai menor que espai 0 fi cel·la fila cel·la f parèntesi esquerre menys 0.8 parèntesi dret espai igual espai parèntesi esquerre menys 0.8 parèntesi dret al cub espai més espai parèntesi esquerre menys 0.8 parèntesi dret espai més espai 1 igual menys 0.312 menor que 0 fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula tanca claus fletxa doble dreta N o espai p o d e m espai a p l i c a r espai e l espai T. espai d e espai B o l z a n o fi estil$

Provem en [-0,8,-0.5]

estil mida 12px espai espai espai obre taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la f parèntesi esquerre x parèntesi dret espai é s espai u n a espai f u n c i ó espai p o l i n ò m i c a espai i espai p e r espai t a n t espai é s espai c o n t i n u a espai e n espai e l espai i n t e r v a l espai claudàtor esquerre menys 0.8 coma espai menys 0.5 claudàtor dret fi cel·la fila cel·la f parèntesi esquerre menys 0.8 parèntesi dret espai igual espai parèntesi esquerre menys 0.8 parèntesi dret al cub espai més espai parèntesi esquerre menys 0.8 parèntesi dret espai més espai 1 igual menys 0.312 menor que 0 fi cel·la fila cel·la f parèntesi esquerre menys 0.5 parèntesi dret espai igual espai parèntesi esquerre menys 0.5 parèntesi dret al cub espai més espai parèntesi esquerre menys 0.5 parèntesi dret espai més espai 1 igual 0.375 major que 0 fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula tanca claus fletxa doble dreta P e l espai T. B o l z a n o espai e x i s t e i x espai u n espai v a l o r espai &quot; c &quot; espai q u e espai espai c espai pertany espai parèntesi esquerre menys 0.8 coma menys 0.5 parèntesi dret espai t a l espai q u e dos punts espai f parèntesi esquerre c parèntesi dret espai igual espai o fi estil

Per tant x≈-0,7 o bé x≈-0,6 o bé x≈-0,5

Provem en [-0,8,-0.6]

estil mida 12px espai espai espai obre taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la f parèntesi esquerre x parèntesi dret espai é s espai u n a espai f u n c i ó espai p o l i n ò m i c a espai i espai p e r espai t a n t espai é s espai c o n t i n u a espai e n espai e l espai i n t e r v a l espai claudàtor esquerre menys 0.8 coma espai menys 0.6 claudàtor dret fi cel·la fila cel·la f parèntesi esquerre menys 0.8 parèntesi dret espai igual espai parèntesi esquerre menys 0.8 parèntesi dret al cub espai més espai parèntesi esquerre menys 0.8 parèntesi dret espai més espai 1 igual menys 0.312 menor que 0 fi cel·la fila cel·la f parèntesi esquerre menys 0.6 parèntesi dret espai igual espai parèntesi esquerre menys 0.6 parèntesi dret al cub espai més espai parèntesi esquerre menys 0.6 parèntesi dret espai més espai 1 igual 0.184 major que 0 fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula tanca claus fletxa doble dreta P e l espai T. B o l z a n o espai e x i s t e i x espai u n espai v a l o r espai &quot; c &quot; espai q u e espai espai c espai pertany espai parèntesi esquerre menys 0.8 coma menys 0.6 parèntesi dret espai t a l espai q u e dos punts espai f parèntesi esquerre c parèntesi dret espai igual espai o fi estil

Per tant x≈-0,7 o bé x≈-0,6

Encara hauríem de provar en un interval [-0,8,-0.7]

$estil mida 12px espai espai espai obre taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la f parèntesi esquerre x parèntesi dret espai é s espai u n a espai f u n c i ó espai p o l i n ò m i c a espai i espai p e r espai t a n t espai é s espai c o n t i n u a espai e n espai e l espai i n t e r v a l espai claudàtor esquerre menys 0.8 coma espai menys 0.7 claudàtor dret fi cel·la fila cel·la f parèntesi esquerre menys 0.8 parèntesi dret espai igual espai parèntesi esquerre menys 0.8 parèntesi dret al cub espai més espai parèntesi esquerre menys 0.8 parèntesi dret espai més espai 1 igual menys 0.312 menor que 0 fi cel·la fila cel·la f parèntesi esquerre menys 0.7 parèntesi dret espai igual espai parèntesi esquerre menys 0.7 parèntesi dret al cub espai més espai parèntesi esquerre menys 0.7 parèntesi dret espai més espai 1 igual menys 0.043 menor que 0 fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula tanca claus fletxa doble dreta E l espai T. B o l z a n o espai n o espai f u n c i o n a fi estil$

Hauríem de provar en un interval [-0,7,-0.6]

estil mida 12px espai espai espai obre taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la taula fila cel·la f parèntesi esquerre x parèntesi dret espai é s espai u n a espai f u n c i ó espai p o l i n ò m i c a espai i espai p e r espai t a n t espai é s espai c o n t i n u a espai e n espai e l espai i n t e r v a l espai claudàtor esquerre menys 0.7 coma espai menys 0.6 claudàtor dret fi cel·la fila cel·la f parèntesi esquerre menys 0.7 parèntesi dret espai igual espai parèntesi esquerre menys 0.7 parèntesi dret al cub espai més espai parèntesi esquerre menys 0.7 parèntesi dret espai més espai 1 igual menys 0.043 menor que 0 fi cel·la fila cel·la f parèntesi esquerre menys 0.6 parèntesi dret espai igual espai parèntesi esquerre menys 0.6 parèntesi dret al cub espai més espai parèntesi esquerre menys 0.6 parèntesi dret espai més espai 1 igual 0.184 major que 0 fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula fi cel·la fi taula tanca claus fletxa doble dreta P e l espai T. B o l z a n o espai e x i s t e i x espai u n espai v a l o r espai &quot; c &quot; espai q u e espai espai c espai pertany espai parèntesi esquerre menys 0.7 coma menys 0.6 parèntesi dret espai t a l espai q u e dos punts espai f parèntesi esquerre c parèntesi dret espai igual espai o fi estil

Per tant x≈-0,6