Recordem conceptes bàsics funcions
| Site: | Cursos IOC - Batxillerat |
| Course: | Matemàtiques II (Bloc 2) ~ gener 2020 |
| Book: | Recordem conceptes bàsics funcions |
| Printed by: | Usuari convidat |
| Date: | Saturday, 18 May 2024, 3:10 PM |
Description
Resum
CONCEPTE DE FUNCIÓ
Una funció és una relació de dependència entre dues magnituds, de manera que a cada valor de la primera magnitud li correspon un únic valor de la segona.
La segona variable depèn del valor de la primera i d'aquí que la primera s'anomena variable independent i la segona variable dependent.
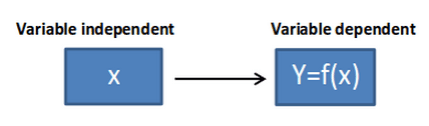
Hi ha moltes maneres d'expressar una funció, per exemple:
-
-
- Mitjançant un enunciat
- Mitjançant una taula
- Mitjançant un gràfic
- Mitjançant una expressió algebraica o fórmula
-
IMATGES I ANTIIMATGES
Quan tenim una funció i un nombre x es relaciona amb un altre nombre y ho expressem dient y=f(x)
Això ho llegiríem dient que y és la imatge de x per la funció f i també que x és una antiimatge de y per la funció f.
Si coneixem l'expressió algebraica de la funció:
-
- Si volem calcular una imatge, f(a), coneixem la x i hem de trobar la y. Haurem de substituir la x per a a l'expressió de la funció i fer els càlculs. Tots els valors del domini tenen una i només una imatge.
- Si volem calcular una antiimatge f-1(b), coneixem la y i volem calcular la x. En aquest cas igualarem l'expressió algebraica a b i aïllarem la x. Pot ser que un valor no tingui antiimatge o més d'una.
Exemples:
Donada la funció calculem la imatge de 2 i l'antiimatge de 0.
Per calcular la imatge de 2, substituirem la x per 2 a l'expressió:
Per tant, podem dir que la imatge de 2 per la funció f és 3/4, i per tant la funció passa pel punt (2, 3/4)
Per calcular la antiimatge de 0 per f, igualarem a 0 l'expressió i aïllarem la x.
Recordeu que una fracció és 0, si ho és el numerador
Això vol dir que 0, té dues antiimatges que són 1 i -1 i per tant la funció passa per (1,0) i (-1,0)
DOMINI
El domini d'una funció f està el formen els valors de la variable independent x que tenen imatge per f. Els representem per Dom f.
Si tenim una funció definida de forma algebraica, per calcular el seu domini haurem de trobar els valors reals on té sentit aplicar la fórmula algebraica, bàsicament caldrà vigilar:
- El domini de les funcions polinòmiques són tots els reals: R
- No podem dividir per zero.
- Les arrels quadrades només es poden aplicar als nombres positius i el zero.
- Els logaritmes només es poden aplicar a nombres positius (el zero no).
Gràficament són els valors horitzontals per on passa el gràfic.
RECORREGUT
El recorregut o rang d'una funció f és el conjunt format per totes les imatges de f, és a dir són tots els valors y que són imatge d'alguna x. El denotem Im f.
Gràficament són tots els valors verticals del gràfic.
Exemple
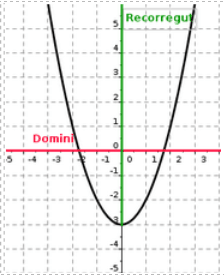 |
A l'esquerra tenim el gràfic d'una funció f(x)=x²-3 En tractar-se d'una funció polinòmica el domini està format per tots els nombres reals, és a dir: Dom f= R Per altra banda observant el gràfic per trobar el recorregut veiem que verticalment pren valors entre -3 i fins a infinit (les branques seguirien creixent, tot i que aquí només en posem un tros), per tant Im f = [-3, +∞) |
Aquest vídeo és interactiu. Conté exemples del càlcul de dominis de funcions i activitats amb les que podreu comprovar si heu entès l'explicació. Per visualitzar-lo bé, cliqueu a sobre del símbol de pantalla completa
|
Exemple: Calculeu el domini de la funció:
|
|---|
Resposta:
En substituir "x" per un nombre real en l'expressió algebraica de la funció, el resultat no sempre és un nombre real.
En aquesta funció concreta, si volem calcular la imatge de per exemple x=0 es veu que
, no és un nombre real.
Com es troba el domini d'aquesta funció que conté una arrel quadrada?
En el cas de funcions amb arrels quadrades o d'índex parell, cal saber que l'arrel quadrada de nombres negatius no dóna un nombre real.
Per tant el domini el componen els valors de "x" que fan que:
Observeu que només per a valors de "x"majors o iguals que 3 es pot calcular la imatge.
En la imatge la línia verda correspon la gràfica de la funció i la part vermella remarca que els valors més grans o iguals que 3 són valors de la "x" que tenen imatge.

FUNCIONS QUE TENEN PER GRÀFICA UNA RECTA
Les funcions que tenen per gràfica una recta són de tipus f(x)=y=mx+n . Aquestes funcions es diuen funcions afins.
El Domf= R i el recorregut també, és a dir Imf=R.
La m es el pendent de la recta i ens indica la inclinació d'aquesta.
- Si la m≥0 la recta és creixent
- Si la m≤0 la recta és decreixent
La n es diu ordenada a l'origen i ens indica el punt de tall de la recta amb l'eix vertical (de les y)
En el cas que la n=0 , la recta té equació f(x)=y=mx aquestes funcions es diuen funcions lineals i tenen la peculiaritat que passen totes elles per l'origen de coordenades.
En el cas que la m=0 la funció queda de tipus f(x)=y=n i en aquest cas la funció és constant, sempre val el mateix i el seu gràfic és horitzontal.
Si coneixem l'expressió d'aquestes funcions per dibuixar-ne el gràfic farem una taula de valors (tot i que amb 2 en tenim prou millor fer-ne 3 o 4 per garantir que no ens hem equivocat), llavors situem els punts als eixos coordenats i els unim formant una recta.
Exemples:
|
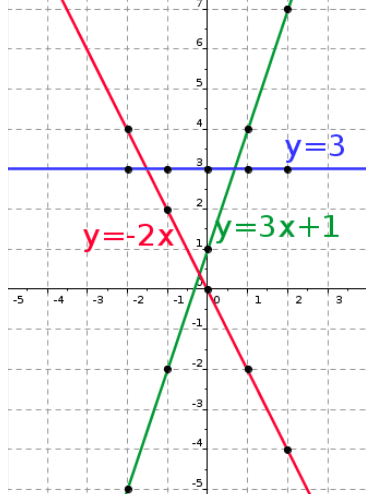 |
||||||||||||||||||||||||||||||||||||||||||||||||||
Si voleu més informació sobre aquest tema podeu llegir aquest document anomenat Funcions afins
FUNCIONS QUADRÀTIQUES
L'expressió algebraica d'una funció quadràtica és un polinomi de grau 2:
Com totes les funcions polinòmiques el Domini està format per tots els nombres reals R
La gràfica sempre és una paràbola de manera que:
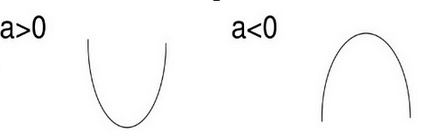
Quan més gran és el coeficient "a" en valor absolut més tancades són les branques de la paràbola.
El vèrtex de la paràbola ve donat per les coordenades :
FUNCIONS RACIONALS
Són aquelles que tenen com a expressió algebraica el quocient de dos polinomis :
El domini d'aquestes funcions està format per R–{x| Q(x)=0} . És a dir el domini són tots els valors reals menys aquells que anul·len el denominador.
Un cas particular d'aquestes funcions són les funcions de proporcionalitat inversa amb k una constant. La seva gràfica és una hipèrbola.
Exemples:
el domini seria en aquest cas R–{3}
el domini seria tot R, perquè en aquest cas per què el denominador no s'anul·la mai.
FUNCIONS IRRACIONALS
Són aquelles en que la x es troba sota el signe de radical.
Ens limitarem a estudiar les que son de tipus amb g(x) una funció racional.
A l'hora de calcular el domini cal tenir en compte:
-
- Si la n és parell Dom f={x| g(x)≥0}
- Si la n és imparell Dom f= Dom g
Exemples:
el domini és tot R perquè l'índex és senar el la funció de dins del radicand és polinòmica, per tant no té problemes de domini
en tenir índex parell, el domini estarà format pels punts que x+2 ≥0, és a dir x ≥-2, els reals més grans o iguals a -2. Dom f=[-2, +∞)
FUNCIONS EXPONENCIALS
Son de tipus f(x)= ax amb "a" un nombre real positiu i diferent de 1.
Les característiques d'aquestes funcions són:
-
- El domini són tots els R
- El recorregut són tots els R positius
- Totes tallen a l'eix de les y en el punt (0,1) perquè a⁰=1 per tot valor del coeficient a
- Si a>1 el gràfic és creixent i quan x pren valors molt petits el gràfic s'acosta a l'eix horitzontal
- Si 0<a<1 el gràfic és decreixent i quan x es fa molt gran el gràfic s'acosta a l'eix horitzontal.

FUNCIONS DEFINIDES A TROSSOS
Diem que una funció està definida a trossos si la seva expressió algebraica no és sempre la mateixa, sinó que varia en funció del valor de la x.
Per trobar el domini hem de calcular el domini de cadascuna de les funcions que la formen, tenint en compte l'interval on aquestes estan definides.
Si volem calcular-ne imatges, haurem de vigilar quina expressió ens cal mirar.
Exemple:
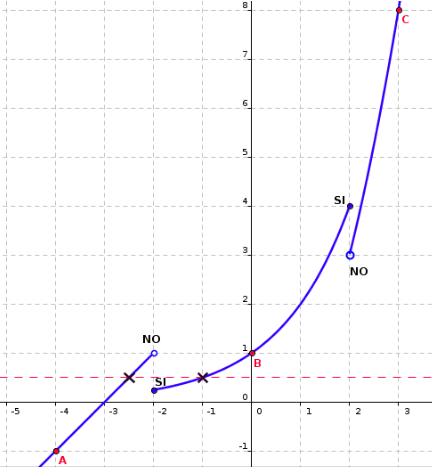
Observa la següent funció, amb la seva expressió algebraica a l'esquerra i el seu gràfic a la dreta amb uns punts assenyalats.
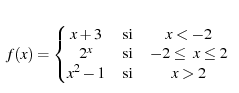 |
 |
Aquesta funció està definida en tres trossos.
Pels valors de x més petits que -2, l'expressió de la funció és la funció afí x+3.
Pels valors de x que estan a l'interval [-2, 2] l'expressió de la funció és l'exponencial 2x.
Pels valors de x més grans que dos la funció té l'expressió quadràtica x²-1
Els punts del gràfic que estan assenyalats com un punt obert o vol dir que no formen part del gràfic.
Així per exemple per calcular la imatge del -2, quina expressió caldria agafar?
La segona, 2x, és per això que el punt (-2, 1) que correspondria a la recta de l'esquerra està assenyalat obert o en canvi el punt (-2, 0.25) que correspon al gràfic exponencial està assenyalat tancat ·.
Com calcularíem la imatge de -4?
Com -4 és més petit que -2, cal agafar la primera expressió x+3 i substituir la x per -4. (-4+3=-1).
Així diríem que la imatge per f de -4 és -1. (punt A)
Com calcularíem la imatge de 0?
Com 0 és més gran que -2 i més petit que 2, cal agafar la segona expressió 2x i substituir la x per 0. (20=1).
Així diríem que la imatge per f de 0 és 1. (punt B)
Com calcularíem la imatge de 3?
Com 3 és més gran que 2, cal agafar la darrera expressió x²-1 i substituir la x per 3. (32-1=8).
Així diríem que la imatge per f de 3 és 8. (punt C)
Té antiimatges 0.5 per la funció f?
Per calcular antiimatges, el millor és mirar el gràfic.
Fixeu-vos que al gràfic s'ha dibuixat una línia puntejada, aquesta és y=0.5. Mirarem si el gràfic talla aquesta recta.
Veiem que sí, dues vegades assenyalades a la imatge amb una creu x. Per tant 0.5 té dues antiimatges -2.5 i -1.
|
1.-Observeu el gràfic següent, d'una funció polinòmica de tercer grau i indiqueu les qüestions següents:
a) Calculeu la imatge de x = 1, i de x = 2 b) Calculeu les coordenades dels punts de tall de la funció amb l'eix X. c) Calculeu les coordenades dels punts de tall de la funció amb l'eix Y. c) Doneu les coordenades del màxim i del mínim relatius de la funció |
Resposta I :
En aquest problema coneixem la gràfica de la funció, per tant podem deduir totes les respostes simplement observant la gràfica
a) Observant la gràfica:
f(1) =0
f(2) =4
b) Punts de tall (-2,0) i (1,0). Són els punts en els que la gràfica toca l'eix X
c) Punts de tall (0,2) . És el punt en el que la gràfica toca l'eix Y
d) Màxim (-1,4) i Mínim (1,0)
Resposta II
Si de la funció només es coneix la seva expressió algebraica ( y= x3-3x+2) i no la seva gràfica, podríem trobar algunes de les respostes.
a) f(1) = 13-3(1)+2=0
f(2) = 23-3(2)+2=4
b) Punts de tall amb l'eix X es resoldria el sistema d'equacions següent :
I s'obté com a solucions x=1 doble, i x=.2. Per tant els punts de tall són (1,0) i (-2,0)
d) Punts de tall amb l'eix Y es resoldria el sistema d'equacions següent :
d) Els màxims i mínims es poden trobar usant la derivada, concepte que encara no hem explicat.
| Una empresa de lloguer de cotxes ofereix dues modalitats de lloguer amb dos tipus de tarifes: TARIFA A: 35€ per dia sense límit de km TARIFA B: 10€ per dia i 0,20€ per km recorregut Un turista vol llogar un cotxe per una setmana, a partir de quants km l'interessa una o l'altra modalitat? |
Resposta
La solució es pot trobar de diferents formes, però una d'elles, seria fer una gràfica de cada una de les situacions, i en els mateixos eixos fet que ens permetrà fer comparacions.
El temps de lloguer és una setmana, per tant les variables a relacionar són x=km recorreguts i y=€ (preu)
Farem una taula de valors que després representarem en us eixos de coordenades.
| Tarifa A | Tarifa B | |||
| x(km) | y(€) | x(km) | y(€) | |
| 200 km | 35·7 =245€ | 200 km | 10·7+0,2·200=110 € | |
| 500 km | 35·7 =245€ | 500 km | 10·7+0,2·500=170 € | |
| 1000 km | 35·7 =245€ | 1000 km | 10·7+0,2·1000=270 € | |
| 2000 km | 35·7 =245€ | 2000 km | 10·7+0,2·2000=470 € | |
| 3000km | 35·7 =245€ | 3000 km | 10·7+0,2·3000=670 € | |
| x km | 35·7 =245€ | x km | 10·7+0,2·x € |
Els valors de "x" els hem triat a l'atzar. Però ens permeten observar que la resposta estarà entre 500 km i 1000km. Provant amb valors entre 500 i 1000 trobarien el nombre de Km a partir dels qual podem deduir quina tarifa és més interessant.
Per calcular exactament aquests km , sens e anar provant, cal resoldre els sistema format per les dues equacions algebraiques de les funcions:
La interpretació d'aquest càlcul és la següent:
Si el client fa menys de 875 km, l'interessa la tarifa A (línia vermella de la gràfica)
SI el client fa exactament 875 km, les dues tarifes representarien el mateix cost.
Si el client fa més de 875 km, l'interessa més la tarifa B (línia blava de la gràfica)
Gràfica: