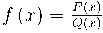Resum de continguts sobre funcions
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques I (Bloc 2) ~ gener 2020 |
| Llibre: | Resum de continguts sobre funcions |
| Imprès per: | Usuari convidat |
| Data: | divendres, 19 d’abril 2024, 04:14 |
Descripció
Resum
Taula de continguts
El concepte de funció
En contextos quotidians i científics ens trobem molt sovint amb la relació de variables: l'espai que recorre una partícula depèn del temps, la pressió de l'aigua del mar depèn de la profunditat, el preu que paguem per una carrera amb taxi depèn dels km recorreguts, ...
Anomenem funció a una relació de dependència entre dues magnituds, de manera que a cada valor de la primera magnitud li correspon un únic valor de la segona.
La segona variable depèn del valor de la primera i d'aquí que la primera s'anomena variable independent i la segona variable dependent.
Hi ha moltes maneres d'expressar una funció, per exemple:
-
-
- Mitjançant un enunciat
- Mitjançant una taula
- Mitjançant un gràfic
- Mitjançant una expressió algebraica o fórmula

-
Imatge de 2
La imatge de 2 per la funció f és 3/4, i per tant la funció passa pel punt (2, 3/4).
I podem dir que la antiimatge de 3/4 és 2.
Antiimatge de 0
Per calcular la antiimatge de 0 per f, igualarem a 0 l'expressió i aïllarem la x.
Una fracció és 0, si ho és el numerador:
Per tant, el 0 té dues antiimatges: 1 i -1
i la funció passa pels punts (1,0) i (-1,0)
El domini d'una funció f el formen els valors de la variable independent x que tenen imatge per f. Els representem per Dom f.
És a dir, són els punts on té sentit definir la funció.
Els dominis s'expressen de diferents formes segons convingui: com a conjunt de punts o com a intervals de la recta real.
Càlcul del domini
Si tenim una funció definida de forma algebraica, és a dir com una fórmula, per calcular el seu domini haurem de trobar els valors reals on té sentit aplicar l'expressió algebraica. Bàsicament caldrà vigilar:
- Si la funció és polinòmica
el domini estarà format per tots els nombres reals
- Si la funció és racional, és a dir és quocient de dos polinomis:
, el domini seran tots els valors reals excepte aquells que anul·len el denominador.
- Si la funció té arrels amb índex parell
, sabem que no està definides en els negatius, per tant caldrà trobar quins valors fan que el radicand sigui negatiu i treure'ls del domini.
- Si la funció té una arrel amb índex senar,
no té cap problema de definició. Per tant
.
- Si la funció és logarítmica (les treballarem més endavant)
, tindrem que
- Per trobar el domini de funcions definides a trossos haurem de calcular el domini de cadascun dels trossos i unir-los. Cal tenir en compte en quina regió està definida cada tros.
- Si la funció és l'operació de diverses funcions (suma, resta, multiplicació, etc) caldrà calcular el domini de cada terme i pel domini final s'hauran de tenir en compte totes les restriccions que surtin de cada tros.
- Si la funció és composició de diversos tipus de funcions, s'haurà de vigilar que totes les components estiguin ben definides així com la composició final.
- Si treballem amb una funció en un context, caldrà imposar també que tingui sentit la funció dins del context.
El recorregut o rang d'una funció f és el conjunt format per totes les imatges de f, és a dir són tots els valors y que són imatge d'alguna x.
El denotem
Gràficament la imatge o recorregut de f la formen tots els valors verticals del gràfic.
Exemples
|
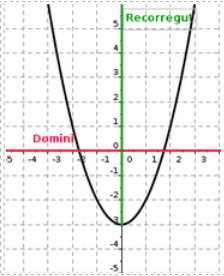
A l'esquerra tenim el gràfic d'una funció f(x)=x²-3 En tractar-se d'una funció polinòmica el domini està format per tots els nombres reals, és a dir: Dom f= R Per altra banda observant el gràfic per trobar el recorregut veiem que verticalment pren valors entre -3 i fins a infinit (les branques seguirien creixent, tot i que aquí només en posem un tros), per tant Im f = [-3, +∞) |
|
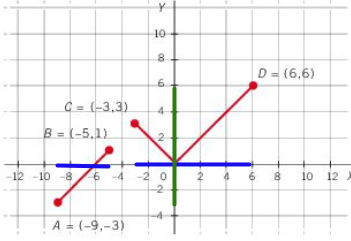
A l'esquerra tenim el gràfic d'una funció a trossos. Per trobar-ne el domini cal veure quins valors de l'eix horitzontal tenen imatge, hem assenyalat en color blau els punts que ho compleixen: Dom f= [-9,-5] U [-3,6] Per altra banda observant el gràfic per trobar el recorregut veiem que verticalment pren valors entre -3 i fins a 6, per tant Im f = [-3, 6] |
A l'hora de calcular el domini i recorregut d'una funció, caldrà tenir en compte si la funció està definida en un context real i llavors restringir-los allà on aquest tingui sentit.
Per exemple, en considerar la funció f(x)= 2x podríem dir que tant el domini com el recorregut d'aquesta funció són tots els reals.
Ara bé, la funció que ens associa l'àrea d'un rectangle de base 2 en funció de l'altura, també seria f(x)=2x en canvi hauríem de pensar que tant el domini com el recorregut són els reals positius, doncs no té sentit pensar en una altura o àrea negatives.
Calculeu el domini de las funcions:
a)
f(x) és una funció polinòmica i per tant (tots els nombres reals).
b)
El denominador és x
El denominador s'anul·la en x=0
c)
El denominador s'anul·la en:
d)
Mirem on s'anul·la el denominador:
e)
Mirem on s'anul·la el denominador:
g)
g(x) és una funció racional. Domini de la funció = R-{valors que anul·len el denominador}
Calculem doncs els valor s que anul·len el denominador:
Per tant:
h)
h(x) és una funció irracional d'índex parell, ja que l'arrel és quadrada.
Domini de la funció = {valors de "x" que fan que el radicand ≥ 0} Cal resoldre la inequació:
podríem posar també
podríem posar també
f(x) és una funció racional, el domini serà tots els nombres excepte els que anul·len el dominador.
Trobem les solucions de l'equació (x-2)·(x+3)=0.
Per tant,
o)
Només hem de tenir en compte que sigui del domini de 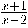
Per tant,
p)
Per tant el domini de f, és el conjunt solució de la inequació
En aquest cas per tal que el radicant sigui positiu també, com en el cas anterior, cal que
però com que a més està en el denominador,
Per tant ha de ser
Expressat en forma d'interval:
(fixeu-vos la diferència de l'interval de l'esquerra tancat en l'exercici anterior, i obert en aquest exercici)
Dominis a les funcions definides a trossos
En una funció a trossos hi ha diferents expressions. Per calcular la imatge per un valor de la x s'utilitza una o altra expressió depenent de les condicions de cadascuna. Llavors el domini està format per tot el conjunt de valors de x els quals tenen imatge
Exemple 1
té 4 trossos.
Intentem buscar imatges per alguns valors de x
f(-4)=(-4)-1=-5 (expressió 1a ja que -4≤-3)
f(-3)=(-3)-1=-4 (expressió 1a ja que -3≤-3)
f(-1)=1/(-1+2) =1 (expressió 2a ja que -3<-1<0)
f(-2)= 1/(-2+2)=1/0 que NO EXISTEIX (expressió 2a ja que -3<-2<0)
f(0)=NO EXISTEIX ja que no compleix cap de les 4 condicions
f(0'5)=(0'5)2+2=2'25 (expressió 3a ja que 0<0'5≤1)
f(1)=(1)2+2=3 (expressió 3a ja que 0<1≤1)
f(3)=5 (expressió 4a ja que 3≥3)
f(4'2)=5 (expressió 4a ja que 4'2≥3)
En definitiva estudiant cadascun dels trossos tenim:
-
- Si x≤ -3 llavors té imatge, la funció és polinòmica i es calcula substituint en l'expressió
- Si
la funció és racional. Llavors té imatge, llevat del cas x= -2, valor on s'anul·la el denominador i es calcula substituint en l'expressió
.
- Si
llavors té imatge ( la funció és polinòmica) i es calcula substituint en l'expressió
- Si x ≥ 3 llavors té imatge i val 5 (la funció és constant)
- Si x≤ -3 llavors té imatge, la funció és polinòmica i es calcula substituint en l'expressió
I per tant el
Exemple 2:
Exemple 3
Aquesta funció té dos trossos diferenciats i fixa't que hi ha un conjunt de punts on no està definida: els valors entre 0 i 2. Perfer imatges de valors negatius ens haurem de mirar el tros de dalt i pels valors més grans o igual que 2 haurem de mirar la funció de baix i pels valors entre 0 i 2 no té expressió.
El primer tros és racional. En principi hem d'evitar dividir per 0. El denominador s'anul·la si x= 3, però en ser un valor positiu la seva imatge es faria aplicant la definició del segon tros, per tant el primer tros està ben definida per tots els negatius.
El segon tros és polinòmic i per tant no té cap problema de definició, està ben definida per tots els valors més grans o iguals a 0.
En definitiva l'únic problema de definició ve donat per com ens han definit la funció. Tenim doncs que
Operacions amb funcions
Amb el conjunt de totes les funcions de variable real, es poden definir les operacions aritmètiques bàsiques. Així, donades dues funcions Suma i resta de funcions
, el seu domini serà
, el seu domini serà
Producte de funcions
, el seu domini serà
Quocient de funcions
, el seu domini serà
Composició de funcions
A més de les operacions aritmètiques, tenim una operació diferent que mereix una especial atenció: la composició de funcions.
Donades dues funcions f(x) i g(x) definim la funció f composta amb g com la funció que resulta d'aplicar primer la funció f i a la imatge resultant aplicar-li g. Aquesta composició es notarà matemàticament
Atenció! observa que es llegeix primer la funció que està escrita més a la dreta, perquè és la que s'aplica en primer lloc.
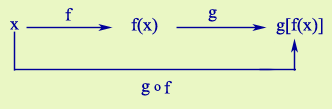
El domini de la funció composició estarà formada per tots els punts del domini de f que tenen la imatge dins del domini de g.
Cal tenim en compte que aquesta operació NO és commutativa, és a dir: en general no és el mateix f composta amb g que g composta amb f.
Exemple
Considerem i
Llavors com és la funció
Apliquem la definició:
Observem que hem fet:
- primer apliquem f a x:
- ara cal aplicar g però a a la variable x²-1 , per tant cal canviar la x de la funció g per x² -1 i fer les operacions que la g indica.
Feu ara al quadern Dona el mateix que abans?
Funció inversa
La funció inversa de f respecte a la composició és l'única funció que, en cas d'existir, verifica
Observeu que la funció inversa la denotem
És a dir:
No sempre existeix la funció inversa, només per a les funcions injectives.
Característiques importants de la funció inversa:
- el domini de la funció inversa
coincideix amb la Imatge de la funció
- la imatge o recorregut de la funció
coincideix amb el domini de la funció
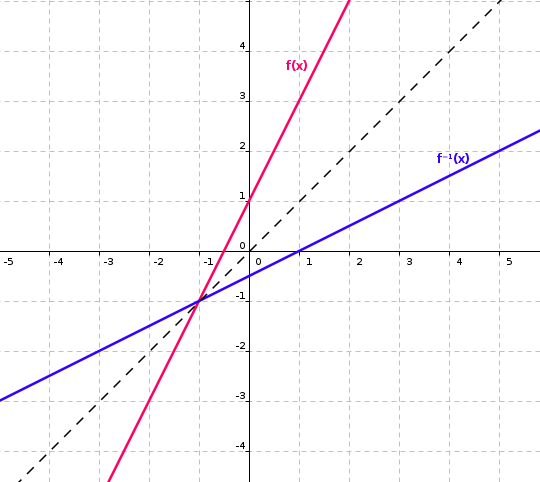
- les gràfiques respectives d'una funció i la seva inversa són simètriques respecte a la recta y=x (bisectriu del primer i tercer quadrant)
Com es calcula la funció inversa?
Què faremper calcular la funció inversa d'una funció f si en coneixem la seva expressió analítica?
Podem seguir aquests passos:
- Igualem l'expressió de f a y.
- Aïllem la x de l'equació anterior en funció de y.
- Canviem la y per la x i ja tenim la inversa.
Vegem un exemple:
Considerem la funció
- Igualem l'expressió a y:
- Aïllem la x en funció de y:
- Canviem la x per la y i li diem f⁻¹ a l'expressió resultant:
Per provar que hem trobat correctament la inversa farem les dues composicions i veurem que donen la identitat de x.
Característiques de les funcions
En estudiar una funció, a més de conèixer-ne el domini i recorregut, hi ha altres característiques d'interès i que ens donaran una idea de com és la seva gràfica.
Hi ha molts programes que fan gràfiques de funcions, per exemple la calculadora wiris i el programa Geogebra.
Manual bàsic de Geogebra per dibuixar gràfics de funcions.
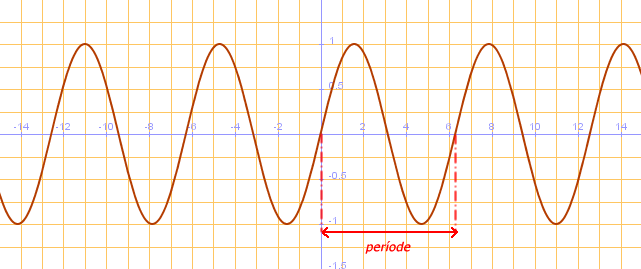
Funcions periòdiques
Una funció és periòdica de període T, si per tot punt del domini es verifica f (x+T)=f(x).
En aquest cas el gràfic de la funció va repetint la seva forma.
Funcions parelles o imparelles (simetries)
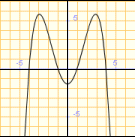
Direm que una funció és parella si per a tot punt del domini es verifica que f(-x)=f(x).
Les gràfiques de les funcions parelles són simètriques respecte a l'eix d'ordenades.
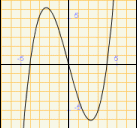
Direm que una funció és senar, si per a tot punt del domini es verifica que f(-x)=- f(x)
Les gràfiques de les funcions senars són simètriques respecte a l'origen de coordenades.
| Parella
|
Senar |
|---|---|
|
|
Punts de tall amb els eixos
Són aquells punts on el gràfic de la funció talla amb els eixos de coordenades.
Punts de tall amb l'eix d'abscisses (de les x)
Seran punts de tipus (a,0). Per calcular-los igualarem la funció a 0 i en buscarem les possibles solucions (si n'hi ha) de l'equació que en resulta.
Pot haver-n'hi o no i també pot haver-n'hi més d'un.
Exemple
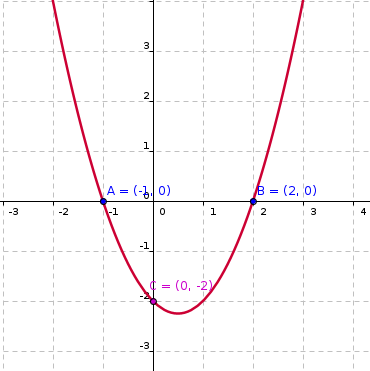
Donada la funció f(x)= x² - x - 2 , per trobar els seus punts de tall amb l'eix de les x, farem:
x² -x - 2 = 0 -----> x= -1 i x= 2
Per tant la funció talla a l'eix d'abscisses en dos punts A=(-1, 0) i B=(2, 0)
Punts de tall amb l'eix d'ordenades (de les y)
Seran punts de tipus (0,b). Per calcular-los només cal calcular la imatge del 0 (sempre que el 0 sigui del domini de la funció). Una funció només pot tallar l'eix vertical en un sol punt, perquè si 0 pertany al domini de f, per definició de funció cada punt té una única imatge.
Exemple
Seguint amb la funció anterior, la imatge del 0 serà f(0)= 0- 0 -2= -2
Per tant el punt de tall és C=(0, -2)
Monotonia i extrems
Una funció monòtona és creixent o decreixent.
- Una funció és creixent en un interval, si sempre que x1 < x2 →f( x1 )
f( x2). És a dir si augmentem el valor de les x, augmenten també les imatges. Observem que les imatges poden ser més grans o iguals.
- Una funció és estrictament creixent en un interval si sempre que x1 < x2 →f( x1 )<f( x2).
- Una funció és decreixent en un interval si sempre que x1 < x2 →f( x1 )
f( x2). És a dir en augmentar el valor de les x, el valor de les imatges disminueix. Observem que les imatges poden ser més petites o iguals.
- Una funció és estrictament decreixent en un interval si sempre que x1 < x2 →f( x1 )> f( x2). És a dir en augmentar el valor de les x, el valor de les imatges disminueix de forma estricta.
Màxims i mínims
L'estudi de la monotonia d'una funció portarà a trobar els possibles màxims i mínims.
Una funció té un màxim relatiu en un punt a, si en un entorn d'aquest punt les imatges són totes més petites o iguals que f(a). Això matemàticament ho escriurem : f(a)
f(x) per a tot x de l'entorn de a.
Una funció té un mínim relatiu en un punt a, si en un entorn d'aquest punt les imatges són totes més grans o iguals que f(a). Això matemàticament ho escriurem : f(a) f(x)
per a tot x de l'entorn de a.
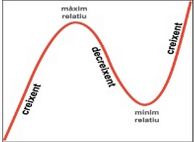
Observa en aquesta imatge que si tenim un màxim relatiu en el punt (a, f(a)) la funció creix a l'esquerra de a i decreix a la seva dreta. Si el que tenim és un mínim relatiu, passa el contrari: la funció a l'esquerra del punt ve decreixent i després passa a créixer.
Atenció! Si en un exercici ens demanin els intervals de creixement i decreixement, no ho haurem d'assenyalar damunt del gràfic, sinó que haurem de dir per quins valors de x (del domini) la funció creix o decreix i ho expressarem en forma d'intervals. Veieu els exercicis resolts dels capítols posteriors.
Funcions fitades
Una funció f està fitada superiorment si hi ha un nombre k tal que per a tot valor x del domini de f es verifica que .
Una funció f està fitada inferiorment si hi ha un nombre k tal que per a tot valor x del domini de f es verifica que .
Les funcions no fitades superiorment (o inferiorment) tenen imatges tan grans (o tan petites) com vulguem.
Exercici
Observeu el gràfic següent, d'una funció polinòmica de tercer grau i indiqueu les qüestions següents:

a) Calculeu la imatge de x = 1, i de x = 2
b) Calculeu les coordenades dels punts de tall de la funció amb l'eix X.
c) Calculeu les coordenades dels punts de tall de la funció amb l'eix Y.
d) Doneu les coordenades del màxim i del mínim relatius de la funció
e) Digueu en quins intervals la funció creix i en quins decreix.
Forma 1
En aquest problema coneixem la gràfica de la funció, per tant podem deduir totes les respostes simplement observant la gràfica
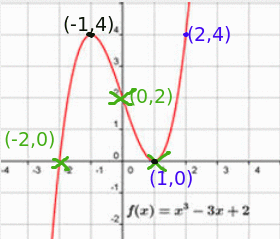
a) Observant la gràfica:
f(1) =0
f(2) =4
b) Punts de tall (-2,0) i (1,0). Són els punts en els que la gràfica toca l'eix X
c) Punts de tall (0,2) . És el punt en el que la gràfica toca l'eix Y
d) Màxim (-1,4) i Mínim (1,0)
e) La funció creix a l'interval i a
i decreix en els punts de l'interval
. (Observeu que els intervals es donen en funció de la x)
Forma 2
Si de la funció només es coneix la seva expressió algebraica ( y= x3-3x+2) i no la seva gràfica, podríem trobar algunes de les respostes.
a) f(1) = 13- 3·(1) + 2 = 0
f(2) = 23- 3·(2) + 2 = 4
b) Punts de tall amb l'eix X . Igualem a 0 la funció i en busquem les arrels. En tractar-se d'una equació de grau 3 cal aplicar el mecanisme de Ruffini.
I s'obté com a solucions x=1 doble, i x=-2. Per tant els punts de tall són (1,0) i (-2,0)
d) Punts de tall amb l'eix Y, només caldria calcular la imatge de 0 per la funció f: f(0)
d) e) Els màxims i mínims i els intervals de creixement es poden trobar usant la derivada, concepte que treballaràs a segon.
Exercici
Una empresa de lloguer de cotxes ofereix dues modalitats de lloguer amb dos tipus de tarifes:
TARIFA A: 35€ per dia sense límit de km
TARIFA B: 10€ per dia i 0,20€ per km recorregut
Un turista vol llogar un cotxe per una setmana, a partir de quants km l'interessa una o l'altra modalitat?
Resolució
La solució es pot trobar de diferents formes, però una d'elles, seria fer una gràfica de cada una de les situacions, i en els mateixos eixos fet que ens permetrà fer comparacions.
El temps de lloguer és una setmana, per tant les variables a relacionar són x=km recorreguts i y=€ (preu)
Farem una taula de valors que després representarem en us eixos de coordenades.
| Tarifa A | Tarifa B | |||
| x(km) | y(€) | x(km) | y(€) | |
| 200 km | 35·7 =245€ | 200 km | 10·7+0,2·200=110 € | |
| 500 km | 35·7 =245€ | 500 km | 10·7+0,2·500=170 € | |
| 1000 km | 35·7 =245€ | 1000 km | 10·7+0,2·1000=270 € | |
| 2000 km | 35·7 =245€ | 2000 km | 10·7+0,2·2000=470 € | |
| 3000km | 35·7 =245€ | 3000 km | 10·7+0,2·3000=670 € | |
| x km | y=245 | x km | y=70+0,2·x € |
Els valors de "x" els hem triat a l'atzar. Però ens permeten observar que la resposta estarà entre 500 km i 1000km. Provant amb valors entre 500 i 1000 trobarien el nombre de Km a partir dels qual podem deduir quina tarifa és més interessant. A
la darrera fila de la taula hem escrit l'expressió algebraica de les funcions
Per calcular exactament aquests km , sens e anar provant, cal resoldre els sistema format per les dues equacions algebraiques de les funcions:
- la primera és constant, val sempre 245 independentment dels km recorreguts
- la segona, és una funció lineal.
Per veure on es tallen les dues funcions resolem el sistema format per les dues expressions.
La interpretació d'aquest càlcul és la següent:
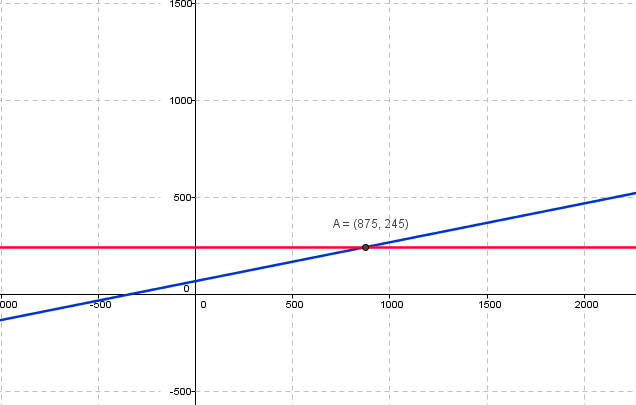
Si el client fa més de 875 km, l'interessa la tarifa A (gràfic horitzontal)
SI el client fa exactament 875 km, les dues tarifes representarien el mateix cost.
Si el client fa menys de 875 km, l'interessa més la tarifa B (gràfic oblic)
Gràfica:
Tipus de funcions
Ens trobarem amb molts tipus de funcions.
Segons la seva expressió algebraica en destaquen:
- funcions polinòmiques (grau 1, grau 2, grau superior)
- funcions racionals o algebraiques.
- funcions irracionals
- funcions exponencials (les veurem amb detall en el lliurament 2)
- funcions logarítmiques (les veurem amb detall en el lliurament 2)
- funcions trigonomètriques
- funcions definides a trossos: valor absolut,...
- ....
Funcions polinòmiques
Un dels tipus més senzills de funcions són les funcions polinòmiques, és a dir les que tenen expressió algebraica de tipus: El domini d'una funció polinòmica de qualsevol grau és sempre tot R.
Detallarem característiques de les funcions polinòmiques de grau 1 i de grau 2, tot i que també és interessant estudiar i representar funcions polinòmiques de grau superior a 2.
Polinomis de grau 1, rectes
Les funcions que tenen per gràfica una recta són de tipus f(x)=y=mx+n , per tant són funcions polinòmiques de grau 1. Aquestes funcions es diuen funcions afins.
El Domf= R i el recorregut també, és a dir Imf=R.
La m és el pendent de la recta i ens indica la inclinació d'aquesta i la velocitat de creixement.
Si la m≥0 la recta és creixent
Si la m≤0 la recta és decreixent
La n es diu ordenada a l'origen i ens indica el punt de tall de la recta amb l'eix vertical (de les y)
En el cas que la n=0 , la recta té equació f(x)=y=mx , aquestes funcions es diuen funcions lineals i tenen la peculiaritat que passen totes elles per l'origen
de coordenades. Aquest tipus de funcions, que constitueixen un cas particular de funcions afins modelitzen les situacions de proporcionalitat directa que sorgeixen molt sovint a la vida quotidiana.
Un altre cas particular de funció afí es dona si la m=0. La funció queda de tipus f(x)=y=n i en aquest cas la funció és constant, sempre val el mateix, no depèn de x i el seu gràfic és horitzontal.
Si coneixem l'expressió d'aquestes funcions per dibuixar-ne el gràfic farem una taula de valors (tot i que amb 2 en tenim prou millor fer-ne 3 o 4 per garantir que no ens hem equivocat). Situem els punts als eixos coordenats i els unim formant una recta.
Exemple
|
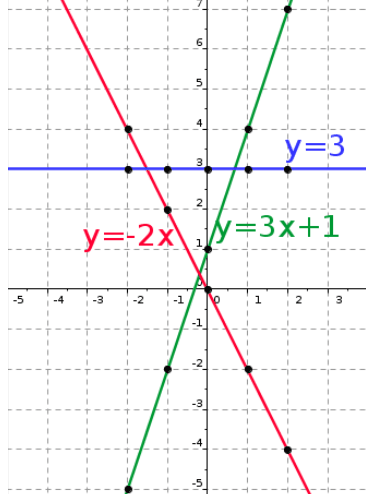
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Es recomana llegir atentament el document:
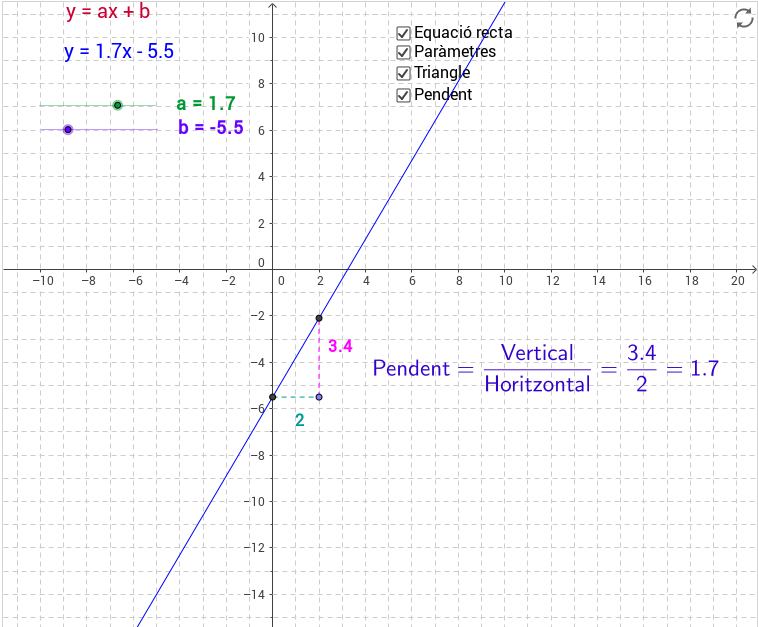
Funció que té per gràfica una recta
Cliqueu després damunt d'aquesta imatge per accedir a un applet fet amb Geogebra per Pep Bujosa. En moure els punts lliscants a i b podreu explorar com varia la gràfica de la recta en fer variar el pendent i l'ordenada a l'origen. Quines conclusions traieu
després d'aquest estudi?
FUNCIONS QUADRÀTIQUES
L'expressió algebraica d'una funció quadràtica és un polinomi de grau 2:
amb a≠ 0
Com totes les funcions polinòmiques el dom està format per tots els nombres reals R
La gràfica és una paràbola.
Gràfica d'una paràbola.
Per fer el gràfic d'una paràbola trobem els seus punts més significatius:
- Talls amb l'eix x La paràbola talla a l'eix x en les solucions de l'equació
- Tall amb l'eix y (0,f(0))
- Vèrtex La coordenada x del vèrtex és
Per trobar la coordenada y, substituïm aquest valor de x en ax2+bx+c
Vèrtex
- Si la paràbola "mira" cap amunt
Si la paràbola "mira" cap avall
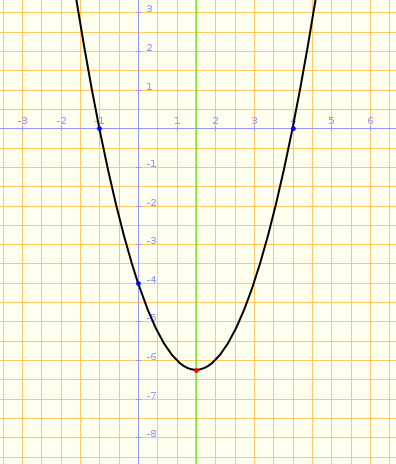
Gràfic de la paràbola
- Talls amb l'eix x
Talls amb l'eix x:
- Tall amb l'eix y
Tall amb l'eix y:
- Vèrtex
Per calcular la coordenada y del vèrtex substituïm en la funció:
Vèrtex
- Gràfica
Observació:
Si el coeficient de la x2 és positiu la paràbola "mira" cap amunt
Si el coeficient de la x2 és negatiu la paràbola "mira" cap avall
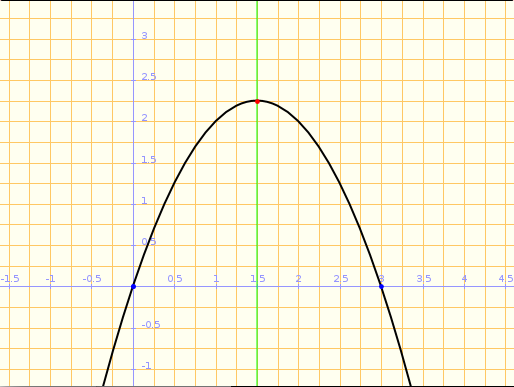
Gràfic de la paràbola
- Talls amb l'eix x
Per resoldre aquesta equació de segon grau incompleta no apliquem la fórmula de l'equació de segon grau
Ho fem més senzill extraient factor comú x:
Talls amb l'eix x:
- Tall amb l'eix y
Tall amb l'eix y:
- Vèrtex
Per calcular la coordenada y del vèrtex substituïm en la funció:
Vèrtex
- Gràfica
Observació:
Si el coeficient de la x2 és positiu la paràbola "mira" cap amunt
Si el coeficient de la x2 és negatiu la paràbola "mira" cap avall
L'evolució de les accions d'una empresa, va seguir , durant l'any passat, aproximadament aquesta funció:
on t és el temps en mesos (0≤t≤12)
f(t) la cotització de les accions en euros.
a) Dibuixa la gràfica.
Com que es tracta d'una paràbola, trobem:
Talls amb l'eix x:
Podem dividir tota l'equació entre 30:
Punts de tall amb l'eix x: (1,0), (7,0)
Tall amb l'eix y: (0, -210)
Vèrtex:
V(4, 270)
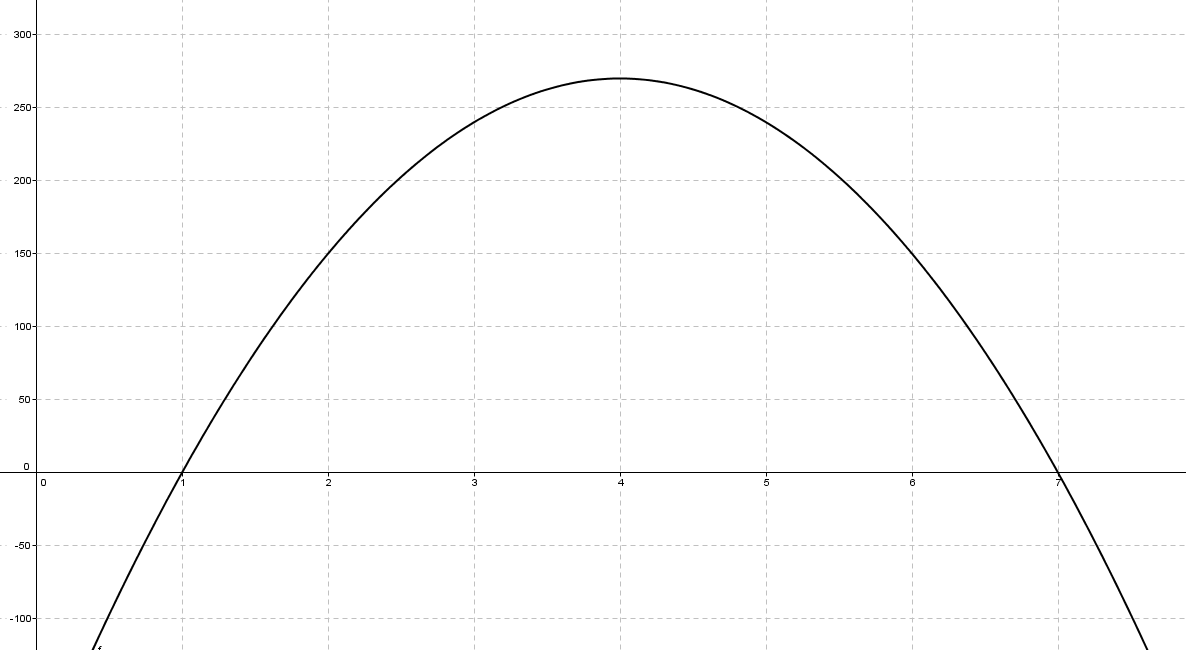
b) En quin mes es va assolir la màxima cotització, i quina va ser aquesta cotització?
En funcions quadràtiques l'extrem (màxim o mínim) s'assoleix en el vèrtex de la paràbola.
En aquest cas, el màxim és el vèrtex de la paràbola, que ja ho hem trobat en el'apartat anterior.
Per tant: la màxima cotització s'assoleix en el mes 4 i és de 270 €.
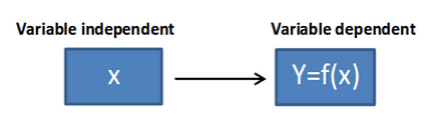
Funcions racionals
Són aquelles que tenen com a expressió algebraica el quocient de dos polinomis
El domini d'aquestes funcions està format per R–{x| Q(x)=0}
És a dir, el domini són tots els valors reals menys aquells que anul·len el denominador. Per calcular els zeros del polinomi del denominador caldrà recordar les tècniques treballades al primer bloc de la matèria: equacions de grau 1, equacions de grau
2, Ruffini...(Podeu repassar-ho a les unitats 1 i 2 del llibre de suport recomanat).
Un cas particular d'aquestes funcions són les funcions de proporcionalitat inversa amb k una constant. La seva
gràfica és una hipèrbola.
Cliqueu damunt la imatge i accedireu a un applet fet amb Geogebra per Juli Jurado de la funció de proporcionalitat inversa . Aneu movent la k, des de -4 fins a 4. Què observeu?
Exemples
-
el domini seria en aquest cas R – {3} ja que x-3=0---->x=3
el domini seria tot R, perquè en aquest cas el denominador no s'anul·la mai. x²+1=0---->x²= -1 i això no té solució en el conjunt de nombres reals.
el domini seria tot R – {-1, 0, 1}, perquè en aquest cas el denominador s'anul·la en aquests tres punts:
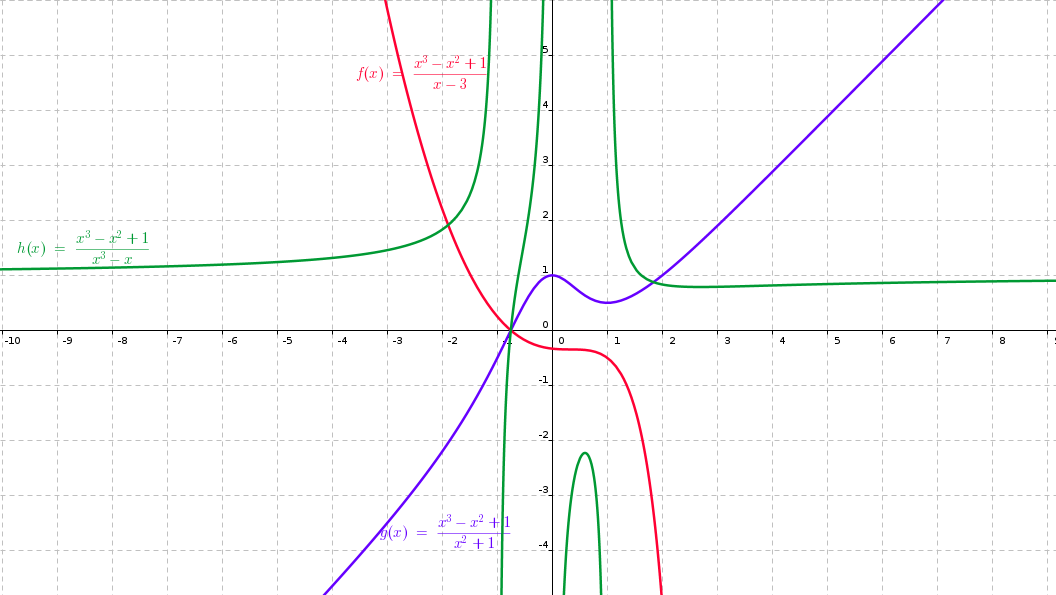
A partir dels gràfics, esbrineu quina seria la Imatge o recorregut de cadascuna de les tres funcions.
Funcions irracionals
Són aquelles en que la x es troba sota el signe de radical.
Ens limitarem a estudiar les que son de tipus
amb
una funció racional.
A l'hora de calcular el domini cal tenir en compte:
- Si la n és parell
(per calcular-ho caldrà resoldre inequacions)
És a dir, si l'índex de l'arrel és par, el radicant ha de ser positiu. - Si la n és imparell
Exemples
el domini és tot R perquè l'índex és senar el la funció de dins del radicand és polinòmica, per tant no té problemes de domini
.
en tenir índex parell, el domini estarà format pels punts que x+2 ≥0, és a dir x ≥-2, els reals més grans o iguals a -2. Dom h =[-2, +∞)
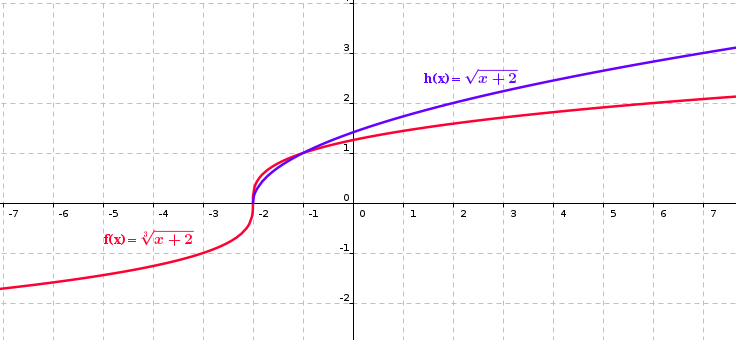
A la imatge anterior podeu veure els gràfics de les dues funcions d'exemple i comprovar els dominis que hem calculat analíticament. A partir dels gràfics deduïu-ne el rang o imatge de cadascuna.
Funcions trigonomètriques
Les funcions trigonomètriques assignen al valor d'un angle (expressat en radians) el valor d'una raó trigonomètrica.
Funcions: sinus, cosinus i tangent
En molts moviments ondulatoris aquestes funcions tenen una gran importància.
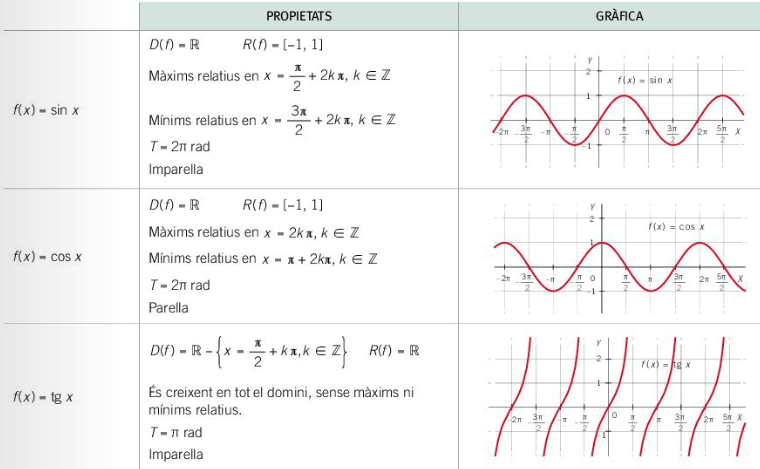
Funcions: secant, cosecant i cotangent
Aquestes són les funcions inverses (respecte a la multiplicació) de les anteriors. En el quadre en podeu veure les característiques principals.

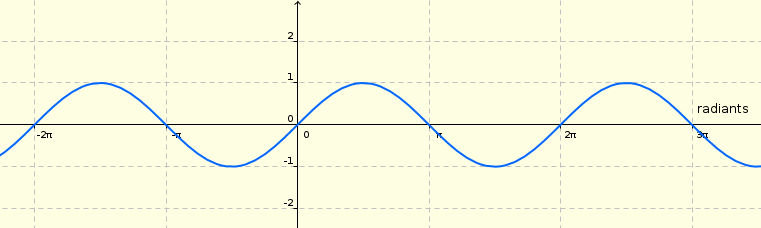
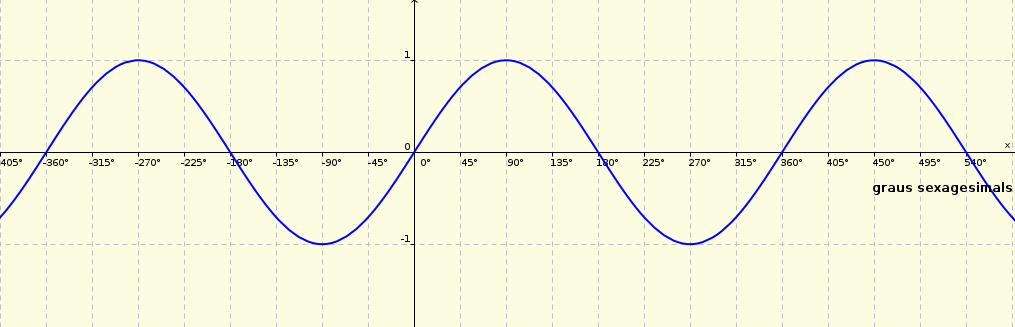
Tot i que en general quan representem funcions trigonomètriques mesurem els angles en radiants, es podria fer amb graus, només hauríem d'ajustar-ho a l'eix de les x.
Exemple
Funcions definides a trossos
Diem que una funció està definida a trossos si la seva expressió algebraica no és sempre la mateixa, sinó que varia en funció del valor de la x.
Per trobar el domini hem de calcular el domini de cadascuna de les funcions que la formen, tenint en compte l'interval on aquestes estan definides.
Si volem calcular-ne imatges, haurem de vigilar quina expressió ens cal fer servir per cada punt.
Exemple
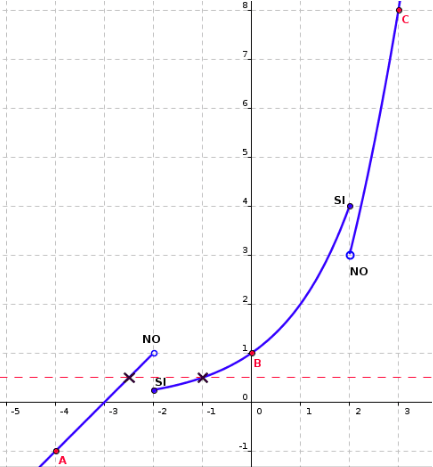
Observeu la següent funció, amb la seva expressió algebraica a l'esquerra i el seu gràfic a la dreta amb uns punts assenyalats.
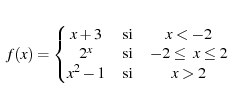
|
|
Aquesta funció està definida en tres trossos.
Pels valors de x més petits que -2, l'expressió de la funció és la funció afí x+3.
Pels valors de x que estan a l'interval [-2, 2] l'expressió de la funció és l'exponencial 2x.
Pels valors de x més grans que dos la funció té l'expressió quadràtica x²-1
Els punts del gràfic que estan assenyalats com un punt obert o vol dir que no formen part del gràfic.
Així per exemple per calcular la imatge del -2, quina expressió caldria agafar?
La segona, 2x, és per això que el punt (-2, 1) que correspondria a la recta de l'esquerra està assenyalat obert o en canvi el punt (-2, 0.25) que correspon al gràfic exponencial està assenyalat tancat ·.
Com calcularíem la imatge de -4?
Com -4 és més petit que -2, cal agafar la primera expressió x+3 i substituir la x per -4. (-4+3=-1).
Així diríem que la imatge per f de -4 és -1. (punt A)
Com calcularíem la imatge de 0?
Com 0 és més gran que -2 i més petit que 2, cal agafar la segona expressió 2x i substituir la x per 0. (20=1).
Així diríem que la imatge per f de 0 és 1. (punt B)
Com calcularíem la imatge de 3?
Com 3 és més gran que 2, cal agafar la darrera expressió x²-1 i substituir la x per 3. (32-1=8).
Així diríem que la imatge per f de 3 és 8. (punt C)
Té antiimatges 0.5 per la funció f?
Per calcular antiimatges, el millor és mirar el gràfic.
Fixeu-vos que al gràfic s'ha dibuixat una línia puntejada, aquesta és y=0.5. Mirarem si el gràfic talla aquesta recta.
Veiem que sí, dues vegades assenyalades a la imatge amb una creu x. Per tant 0.5 té dues antiimatges -2.5 i -1.
Una funció definida a trossos és una funció que no està definida amb la mateixa forma algebraica per a tots els seus punts.
Exemple:
O també la podríem expressar així:
Punts d'aquesta funció. Per exemple:
Observacions:
- En l'interval
posem interval tancat per la dreta per tal d'incloure l'1 ja que volem tots els valors
- En l'interval
posem interval obert per la dreta per tal de no incloure l'1 ja que volem tots els valors
- En els extrem infinits sempre posem interval obert, ja que
no és cap nombre
- En els exemples anteriors no hem pogut fer el cas x=3 ja que seria f(3)=1/0 però 1/0 no és cap nombre
Domini d'aquesta funció
- En l'interval com que la funció
és una recta, tots els punts de l'interval són del domini
- En l'interval , el domini de la funció
és tots els nombres reals excepte el 3
Com que el 3 està en en l'interval , ho hem d'excloure del domini total de la funció f(x)
Per tant:
La gràfica de la funció és aquesta:
(f(x)=x sí ho sabeu dibuixar però no encara f(x)=1/(x-3))
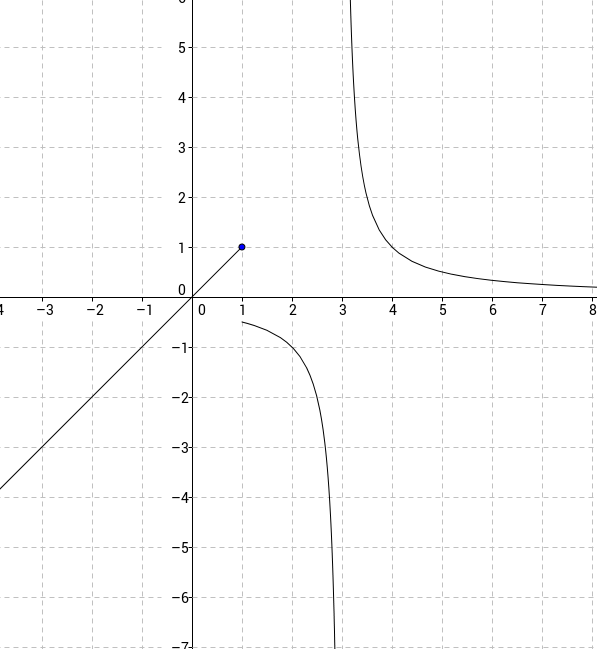
Observació:
Mireu la diferència en el domini d'aquesta altra funció:
En aquest cas x=3 sí és del domini de la funció ja que com que
f(3) = 3
Per tant, en l'únic valor de x que podria haver problema, x=3, no hi ha ja que per a aquest valor la funció és f(x)=x
La gràfica de la funció (encara no la sabeu trobar) és aquesta:
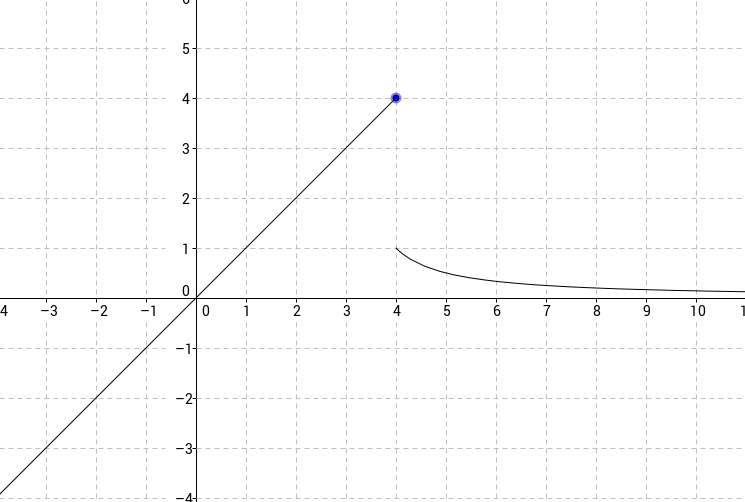
La funció valor absolut
El valor absolut d'un nombre, és el valor sense signe, és a dir sempre positiu. Les funcions on intervé el valor absolut sempre tindran imatges positives.
Les podrem transformar en una funció definida a trossos de la següent manera:
És a dir, cal mirar la funció que està dins del valor absolut. En els punts on aquesta és positiva, el valor absolut de la funció coincideix, per tant no hem de fer cap canvi. Però en els punts on és negatiu, la funció valor absolut li canvia el signe per transformar-la en positiu.
El primer que haurem d'estudiar amb les funcions d'aquests tipus, és el o els valors que anul·len la funció de dins del valor absolut i a partir d'aquí veure que passa als dos costats d'aquest punt.
Exemple
Fer el gràfic i un estudi complet de la següent funció i escriu-la com a funció definida a trossos.
Per valors inferiors a -5 la funció és negativa i per valors més grans que -5 és positiva, per tant aquesta funció es pot escriure com a funció definida a trossos de la següent manera:
Quin és el domini d'aquesta funció? En aquest cas tots els reals, perquè els dos trossos són polinòmics.
Per fer-ne el gràfic observem que els dos trossos corresponen a funcions polinòmiques de grau 1, per tant rectes.
Podem fer una taula de valors de per situar diversos punts del gràfic i unir-los (cal vigilar quin tros correspon a cada imatge).
-
x
-7
-6
-5
4
3
0
f(x)
2
1
0
1
2
5
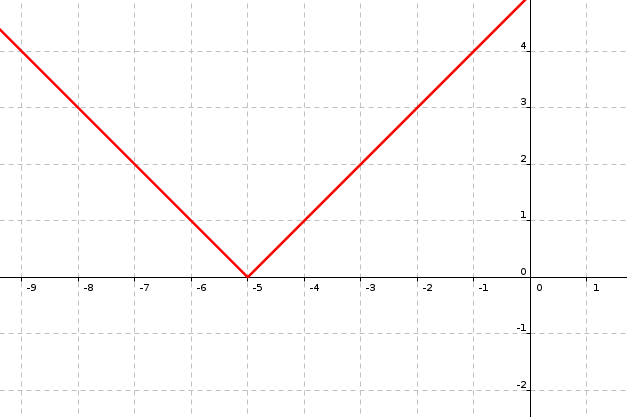
La funció decreix de -∞ a -5 i creix de -5 a +∞.
La funció presenta un mínim relatiu i absolut en el punt (-5, 0)
El punt de tall amb l'eix d'abscisses el trobem en (-5, 0) i el punt de tall amb l'eix d'ordenades el tenim en (0,5) (per trobar-lo cal trobar la imatge de 0 f(0)=0+5=5).
Aquesta funció no és parella, però sí que presenta una simetria respecte a la recta x=-5.