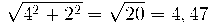Resum conceptes bàsics del lliurament
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques I (Bloc 1) ~ gener 2020 |
| Llibre: | Resum conceptes bàsics del lliurament |
| Imprès per: | Visiteur anonyme |
| Data: | diumenge, 19 de maig 2024, 10:53 |
Descripció
Resum conceptes bàsics del lliurament 5 de Matemàtiques 1 Bloc 1: tema Rectes i circumferències.
Rectes en el pla
Una recta ve determinada:
-
-
- Dos punts: donats dos punts, existeix una única recta que passa per ells
- Un punt i una direcció: la direcció pot venir donada pel vector director, per l'angle d'inclinació o bé per la pendent de la recta.


-
Equacions de la recta
Una equació de la recta és una igualtat que verifiquen tots els punts de la recta i només aquests.
Tenim diverses formes d'expressar aquesta equació. En donem aquí un quadre resum.

Nota: Si en lloc de tenir punt i vector, comencem amb dos punts de la recta P(p1, p2) i Q(q1, q2) construïm el vector director amb origen i extrem aquests dos punts =(q1-p1,
q2-p2) i ja tenim punt P i vector
.
És important distingir els diferents tipus d'equació i saber quina és l'equació més fàcil d'obtenir depenent de quines dades es disposa. Després s'haurà d'operar fins a arribar al tipus d'equació que demani l'exercici.
El vector director d'una recta ens marca la direcció d'aquesta. Qualsevol vector paral·lel indica la mateixa direcció, per tant podem utilitzar qualsevol múltiple del vector si ens és més còmode. Per exemple si el vector director d'una recta fos ,
el podríem multiplicar per 15 per eliminar denominadors i continuaria essent un vector director de la recta :
.
En canvi les coordenades dels punts, no es poden multiplicar perquè deixarien de ser el mateix punt.
Exemple
Considerem la recta r que passa pel punt P=(-1,5) i té com a vector director Al llarg de l'exemple farem servir la notació:
Equació vectorial
Un punt qualsevol de la recta r (x,y) ha de verificar:
amb k un nombre real qualsevol.
Per tant, l'equació vectorial de la recta r en components és:
Equació paramètrica
Ha de ser de tipus:
A partir de l'equació anterior, separarem les dues components i obtenim les equacions paramètriques de la recta:
Equació contínua
Ha de ser de tipus:
A partir de l'equació paramètrica anterior, aïllarem la k de les dues equacions i després les igualarem.
Aïllant la k de la primera equació tenim:
Aïllant la k de la segona equació tenim:
Igualant les dues expressions anteriors tenim l'equació contínua de r.
Si ho fem directament sense venir de l'equació paramètrica, sabent només el punt i el vector, hem de recordar que als numeradors hem de restar les dues coordenades del punt i al denominador hem de posar les dues components del vector.
Equació general o implícita
L'equació general o implícita és de tipus Ax+By+C=0.
Com la podem trobar a partir de l'equació contínua?
A partir de l'equació contínua anterior només hem d'eliminar els denominadors (multiplicant en creu), operar i transposar tots els termes a un mateix costat de la igualtat.
Com la podem trobar a partir del punt i vector inicials?
En aquest cas hem de tenir clar que l'equació general és de la forma .
Observeu que de forma ràpida els coeficients de la x i de la y de l'equació general surten de girar les coordenades del vector director i una d'elles de signe. O dit d'un altre manera, els coeficients de x i de y defineixen un vector perpendicular al
vector director.
Ax+ By+ C=0 -------> seria un vector perpendicular a la recta i
seria un vector director de la recta.
Anem al nostre cas. Tenim que el vector director és
per tant d'entrada sabem que la recta serà de tipus
(observeu,
components girades i una canviada de signe).
Ara ens faltaria trobar la C, però només caldrà imposar que la recta passi pel punt que ens han dit P=(-1,5)
Per tant
Equació punt-pendent
Ara trobarem l'equació punt pendent de la recta r
L'equació punt pendent és de tipus y – p2= m(x – p1) i m= v2/v1
En aquest cas, p1 = -1 , p2 = 5 i (m=6/(-3)=-2)
y –(5)=-2·(x – (-1))
Equació explícita
A partir de l'equació anterior, només cal aïllar la y i reduir l'expressió que en resulta fins obtenir l'equació explícita que és de tipus: y = mx + n
y-5=-2x-2
Observacions:
- S'hauria pogut simplificar des del principi el vector director i en lloc de fer servir el (-3, 6) dividir-lo per 3 i treballar amb el (-1,2)
- Qualsevol de les equacions que hem trobat de la recta la defineixen unívocament i per tant totes són vàlides. Cal saber trobar-les totes i passar d'un tipus a un altre.
Vídeo interactiu: equacions de la recta
Amb aquest vídeo d'onze minuts del canal Unicoos podeu aprendre de forma interactiva com construir els diferents tipus d'equacions de la recta en el pla.
A sota trobareu la barra de navegació com a la imatge, per a la correcta visualització poseu pantalla completa (1)

- doneu-li al play (2), també podeu parar-lo si interessa
- (3) és un índex que us permetrà saltar a una secció concreta si us interessa
- podeu avançar si no voleu veure'l sencer movent el cursor (4)
- cada vegada que trobeu una petita rodoneta lila (5) sortirà una pregunta per practicar el que s'acaba d'explicar, cal que cliqueu el botó que ho indica
 . Les preguntes són de diferents tipus: omplir forats amb un nombre, arrossegar, seleccionar la resposta correcta, etc.
. Les preguntes són de diferents tipus: omplir forats amb un nombre, arrossegar, seleccionar la resposta correcta, etc. - Al final del vídeo hi trobareu un seguit de preguntes seguides a mode de resum.
- Si no voleu respondre a les preguntes, podeu tirar endavant el vídeo.
Posició relativa de dues rectes
Si t'imagines 2 rectes en el pla (per exemple situa dos llapis damunt la taula), és fàcil veure que només es poden donar tres situacions:
- que es tallin en un punt (direm rectes secants)
- que siguin paral·leles i per tant no es tallin mai.
- que siguin la mateixa recta.
Veiem en aquesta taula com podem distingir les tres situacions si tenim informació algebraica en lloc del dibuix de les rectes. Ho podrem veure a partir del vector director i punts en comú, el pendent i els coeficients de la x i de la y a l'expressió general.
Dues rectes en el pla poder ser: |
vectors directors de les rectes |
punts en comú |
Relació entre els pendents |
Equació generalAx+By+C=0A'x+B'y+C'=0 |
|
|
|
Han de ser iguals o proporcionals |
Cap punt en comú | El mateix pendent | ||
|
|
No proporcionals |
Un sol punt en comú | Diferent pendent | ||
|
|
Han de ser iguals o proporcionals |
Tots els punts són comuns | El mateix pendent |
Exercici 1: posició relativa entre rectes
Donada les rectes: que passa per A=(0,1) i B=(3,5) i
.
Procediment :
Comencem trobant l'equació general de la recta r
Ho podem fer de moltes maneres, per exemple la que aquí proposem.
vector director de és
I prenem el punt A=(0,1) per escriure l'equació contínua de la recta:
Passem a forma general o implícita.
Traurem denominadors i l'escriurem en forma ax+by+c=0
multipliquem en creu i simplifiquem:
Passem tot a l'esquerra i queda: expressió general de la recta r
Podem per tant fer l'estudi a partir d'aquestes dues expressions.
Compararem la raó entre els seus coeficients
Clarament en aquest cas
Càlcul del punt de tall
Senzillament caldrà resoldre el sistema format per les equacions de les dues rectes. Es tracta d'un sistema lineal de dues equacions i dues incògnites. Podem fer servir qualsevol dels mètodes coneguts: substitució, igualació o reducció.
Ara sumem les dues equacions i desapareixen les x
aïllem la y;
.
Un cop tenim la y tornem a qualsevol de les dues equacions inicials i la substituïm pel valor obtingut per a trobar la x.
treballem
amb aquesta equació de primer grau.
Ja tenim la solució del sistema
El sistema és compatible determinat perquè té una única solució.
Això vol dir que les dues rectes secants es tallen en el punt
i amb això hem acabat l'exercici.
Exercici 2: equació de la recta paral·lela a una donada
Donada la recta r, d'equació
-3x+4y=11 , i els punts P=(0,-5) i Q=(-1,-8) es demana:
a) trobar raonadament l'equació
de la recta s , paral·lela a r , que passa per P.
b) trobar raonadament l'equació de la recta t perpendicular a s i que passi per Q.
Procediment
a)
Com en aquest cas no especifiquen quin tipus d'expressió de la recta s hem de donar, ho farem de dues maneres.
Trobarem directament l'equació general
Les equacions generals de dues rectes paral·leles tenen els coeficients A i B proporcionals i el C ja no.
Per tant si busquem una recta paral·lela a r podem pensar d'entrada que serà de tipus
-3x+4y+C=0 (observeu que deixem les coeficients de la x i la y iguals) i només cal trobar la C imposant que aquesta recta passi pel punt P=(0,-5)
Busquem el valor de C, substituint les (x, y) per les coordenades del punt P(0,-5)
Finalment l'equació general de la recta 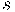 és :
és :
serviria també qualsevol múltiple d'aquesta equació.
Trobarem directament l'equació contínua
- Trobem el vector director de la recta r, sabem que és (B, -A) és a dir (4, 3).
- Qualsevol recta paral·lela a aquesta té el mateix vector director perquè té la mateixa direcció, per tant la recta que cerquem té el vector director (4, 3) i passa per P=(0,-5) per tant a partir d'això podem trobar la recta en forma contínua senzillament substituint.
b) Ho farem també de dues maneres.
Trobarem directament l'equació general
Donada una recta de general Ax+By+C=0, una recta perpendicular serà de tipus Bx-Ay+C' =0 , és a dir té els coeficients de x i y canviat i un d'ells canviat de signe.
Per tant si busquem una recta perpendiular a r podem pensar d'entrada que serà de tipus
4x+3y+C=0 (observeu
que hem fet amb els coeficients de la x i la y ) i només cal trobar la
C imposant que aquesta recta passi pel punt Q=(-1,-8)
Busquem el valor de C, substituint les (x, y) per les coordenades del punt Q=(-1,-8)
Finalment l'equació general de la recta és :
serviria també qualsevol múltiple d'aquesta equació.
Trobarem directament l'equació contínua
- Trobem el vector director de la recta t. Com r és -3x+4y=11 sabem que (-3, 4) és un vector perpendicular a ella, per tant serveix com a vector director de t.
- El vector director de t serà (-3, 4) i passa per Q=(-1,-8) per tant a
partir d'això podem trobar la recta en forma contínua senzillament
substituint.
Punt de tall amb els eixos
Una recta que no sigui ni horitzontal ni vertical, tallarà els eixos de coordenades en dos punts. Un per cada eix. Observeu la imatge:

Aquest punts s'obtenen resolent dos sistemes d'equacions:
-
- Punts de tall amb l'eix X:

-
- Punts de tall amb l'eix Y:

Exercici: punt de tall amb els eixos
Donada la recta r, d'equació 8x-3y+24=0 es demana:
a) Troba els punts de tall de la recta r amb l'eix OY i amb l'eix OX
b) Amb els resultat de l'apartat a) representar gràficament r.
Resolució:
a)
Comencem trobant el punt de tall amb l'eix d'abscisses OX
Per calcular els punts de tall amb l'eix OX, cal resoldre els sistema d'equacions format per la recta i per l'eix OX que té per equació: y = 0
-
- 8x-3y+24=0
- y = 0
Resolem el sistema anterior: la y ja sabem que és 0, només cal trobar la x substituint la y per 0 a la primera equació 8x-3·0+24=0---->8x= -24---->x=-3
S'obté: x=-3 i y=0
Les coordenades del punt de tall de la recta amb l'eix OX és (-3,0)
Ara calculem el punt de tall amb l'eix d'ordenades OY
Per calcular els punts de tall amb l'eix OY, cal resoldre els sistema d'equacions format per la recta i per l'eix OY que té per equació x = 0
-
- 8x-3y+24=0
- x = 0
Resolem el sistema anterior: la x ja sabem que és 0, només cal trobar la y substituint la x per 0 a la primera equació 8·0-3·y+24=0---->-3y= -24---->y=8
S'obté: x= 0 i y=8
Les coordenades del punt de tall de la recta amb l'eix OY és (0,8)
b)
Com ja tenim dos punts de la recta en tenim prou per dibuixar-la, però podem fer-ne un altre per estar més segurs que no ens hem equivocat (recordar que cal que quedin alineats)
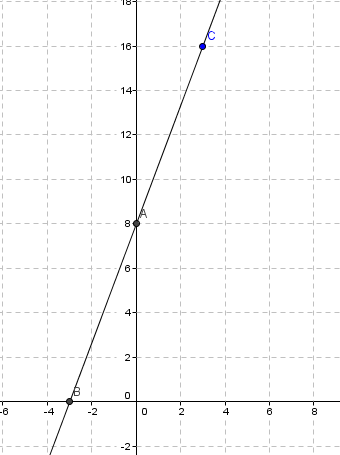
Per exemple prenem x=3 i substituint en l'equació per aïllar la y: 8·3-3y+24=0-----> -3y= -48---->y=16.
La recta passa per (3, 16)
La representació gràfica de la recta és:
Rectes perpendiculars
Dues rectes són perpendiculars si ho són els seus vectors directors.
Si tenim un vector
Observeu que
Si tenim l'equació d'una recta en forma general :Ax+By+C=0----->el vector
Exemple
Donada la recta r, d'equació 2x+y=7 , i el punt P=(1,0), es demana:a) trobar raonadament l'equació de la recta s, perpendicular a r , que passa per P
b) trobar el punt Q on es tallen totes dues rectes.
a) A partir de l'equació general de r: 2x+y=7 i observant els coeficients de "x" i de "y" es poden obtenir les coordenades d'un vector normal (perpendicular) a r
La recta s vindrà definida pel punt P=(1,0) i aquest vector director (2,1)
Equació contínua de la recta s
Fent càlculs en aquesta equació obtenim l'equació general de la recta s : x - 2y - 1 = 0
b) Trobem, ara, el punt Q d'intersecció entre la recta s i la recta r:
Es resol el sistema de les dues equacions generals de r i s, per obtenir Q
-
-
- 2x + y = 7
- x - 2y - 1 = 0
-
En tractar-se d'un sistema lineal de dues equacions amb dues incògnites el podem resoldre per qualsevol dels mètodes coneguts (substitució, igualació o reducció) i resulta ser Q = (3,1).
Comprovem-ho.
Ho fem per reducció, multipliquem la primera equació per 2 i deixem la segona igual.
Ara sumem les dues equacions per eliminar les y.
Finalment tornem a la primera equació (per exemple) substituïm la x per 3 i aïllem la y.
Ja tenim el punt on es tallen les dues rectes.
Angle entre dues rectes.
Dues rectes secants formen 4 angles iguals dos a dos. Els angles diferents sumen 1800
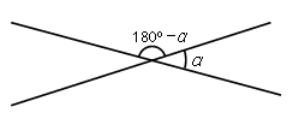
Exemple: angle entre rectes
Determina l'angle que formen les rectes r i s.
Procediment :
1.- Feu un dibuix esquemàtic de la situació
Sabem que l'angle entre dos rectes es calcula a partir de la fórmula:
2.- Trobem els vectors directors de les rectes r i s
De la recta r surt directe de l'equació vectorial que ens donen
Per trobar el vector director de s tenint en compte que tenim l'equació en forma explícita, va bé recordar que el pendent de la recta compleix
En el nostre cas el pendent és
per tant el vector director té direcció donada per
. Podem treballar amb aquest vector
sense problemes però com qualsevol múltiple d'aquest vector també té la mateixa direcció, podem agafar el vector
si ho preferim o qualsevol altre múltiple, sempre procurem agafar-lo el més senzill possible.
Nota: per trobar un vector director també hauríem pogut trobar dos punts de la recta i després les coordenades del vector
.
3.- Calculem el producte escalar dels dos vectors: =|(-4,1)·(-3,1)|=|12+1 |=|13|=13
4.- Calculem els mòduls dels dos vectors :
5.- Calculem el cosinus aplicant la fórmula
Utilitzant la calculadora obtenim l'angle
Distància entre dos punts
La distància entre dos punts ve donada pel mòdul del vector que formen els dos punts.
Per tant si tenim dos punts M =(a,b) i N =(c,d). Per calcular la distància entre ells, construirem el vector.
Distància entre un punt i una recta

- trobar la recta s perpendicular a r que passa per P
- buscar la intersecció de la recta anterior s amb la recta r, és a dir el punt M a la imatge.
- Calcular el mòdul del vector
per trobar la distància demanada.
Aquest procediment és una mica llarg, per això tindrem una fórmula que ens servirà per fer aquest càlcul de forma més ràpida.
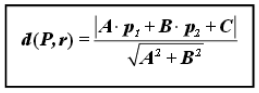
Distància entre dues rectes
La distància entre dues rectes, és la menor de les distàncies entre un punt de r i un altre de s.
Si les dues rectes són secants o coincidents, la distància és 0 perquè tenen un punt (o tots) en comú.
Si les dues rectes són paral·leles, cal trobar un punt P qualsevol de "r" i calcular la d(P,s) aplicant la fórmula anterior. És a dir, la distància entre dues rectes paral·leles és la distància d'un punt qualsevol de la primera recta a la segona.

Simètric d'un punt respecte d'un altre punt.
El simètric d'un punt P respecte d'un altre Q és el punt P' de la recta que formen P i Q de manera que: d(P,Q)=d(Q, P').
Per tant Q és el punt mitjà del segment determinat per P i P'.
Per trobar P' és suficient imposar que

Simètric d'un punt respecte a una recta
El simètric d'un punt P respecte a una recta r, és un altre punt P' complint que la recta que determina P i P' perpendicular a r i els dos punts equidisten de r.
És a dir d(P, r)= d(P', r)

Què hem de fer per trobar-lo?
- Fem un dibuix esquemàtic que il·lustri la situació.
- Trobem l'equació de la recta s perpendicular a r que passa per P.
- Trobem el punt d'intersecció entre les dues rectes, diem-li Q.
- Veiem que Q és el punt mig entre P i el P' que busquem, per tant coneixent P i Q, ja ho tenim tot per trobar el P'.
Exemple 1: distància entre dos punts
Quina és la distància entre els punts A(3,2) i B(7,4)?
Per trobar la distància entre A(3,2) i B(7,4) trobarem les coordenades del vector i en calcularem el mòdul.
Observeu a partir de la imatge que això és equivalent a aplicar el Teorema de Pitàgores.
=(7-3, 4-2)=(4, 2)

Exemple 2: distància entre punt i recta
Sigui P=(3,2) i r la recta -2x+4y+10=0 . Quina distància hi ha entre el punt i la recta?
Apliquem la fórmula:

En el cas que ens ocupa A=-2, B=4 C=10 , p1 = 3 i p2 = 2
u.
Lloc geomètric
Li diem lloc geomètric al conjunt de punts que verifiquen una certa propietat geomètrica.
Mediatriu d'un segment
Donat un segment , la seva mediatriu és el lloc geomètric dels punts del pla que tenen la mateixa distància als dos extrems del segment. Aquests punts formen una recta perpendicular al segment que divideix al segment en dues meitats.

Tenim diferents formes de trobar la mediatriu d'un segment.
1. Una d'elles és agafar un punt P(x,y) qualsevol i resoldre l'equació que surt d'igualar d(P,A)=d(P,B)
2. Un altre forma seria trobant el punt mitjà del segment i trobant la recta perpendicular al segment que passa pel punt mitjà.
Exemple
Trobar la mediatriu del segment AB, essent A=(1,2) i B=(2,5)
Calcularem la distància d'un punt P(x,y) qualsevol a A, també a B i les igualarem. D'aquí en trobarem l'equació de la mediatriu cercada.
Igualem les dues distàncies
Si dues distàncies són la mateixa, els seus quadrats també, per això elevem al quadrat els dos membres de la igualtat per eliminar les arrels.
Proveu fer-ho amb el segon mètode indicat i comproveu que dona la mateixa recta.
Les còniques
Anomenem superfície cònica de revolució al resultat de girar una recta (generatriu) al voltant d'un altre recta (eix) a la qual talla en el punt V que anomenem vèrtex.

En tallar una superfície cònica de revolució amb un pla obtenim seccions còniques que poden ser de 4 tipus segons la posició relativa del pla respecte a la superfície de revolució.
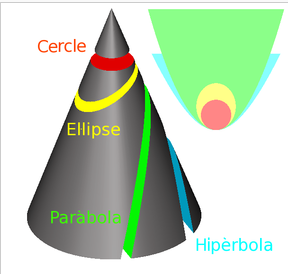
Mira aquest vídeo per acabar d'entendre aquestes definicions.
Podem estudiar les còniques des de diferents punts de vista.
- Com a intersecció de plans amb una superfície cònica de revolució.
- Com a a casos particulars d'equacions de segon grau amb dues variables.
- Com a llocs geomètrics, és a dir punts que verifiquen unes determinades propietats.
Aquest és un tema molt extens, però en aquest curs només es demanarà saber treballar amb les circumferències i saber identificar les equacions dels altres tipus de còniques: les paràboles, el·lipses i hipèrboles.
La circumferència
La circumferència és el lloc geomètric format pels punts del pla que equidisten d'un cert punt C anomenat centre.
Aquesta distància constant la coneixem com a radi.
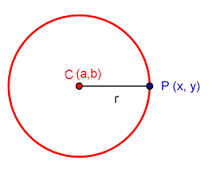
Si P(x,y) és un punt qualsevol de la circumferència i C=(a, b) n'és el centre, tenim que la distància entre ells és
i si elevem al
quadrat aquesta expressió obtenim l'equació analítica de la circumferència:
Desenvolupant els binomis d'aquesta expressió arribem a l'equació general de la circumferència que és de la forma:
Observem que desenvolupant l'equació analítica tenim :
Igualant les dues expressions tenim la relació entre els coeficients de l'equació general i les coordenades del centre i el radi:
Exemples
1. Quin és el centre i el radi de la circumferència
?
Com en aquest cas tenim l'expressió analítica, és molt senzill determinar-ne el centre i el radi.
-----> El centre és doncs C=(-1, 0) i el radi 6.
2. Quin és el centre i el radi de la circumferència
?
En aquest cas tenim més feina, doncs l'equació està en forma general i no és tan directe trobar-ne el centre i el radi.
m= -4 ; n= 10 i p=13
per tant si li diem (a, b) a les coordenades del centre i r al radi cercat tenim aquesta relació:
El centre de la circumferència és i el radi
.
Posició relativa entre punt i circumferència
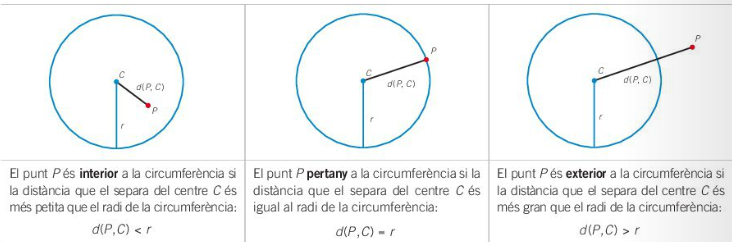
Donat un punt P i una circumferència de centre C i radi r, es poder donar aquestes tres situacions.
- Que el punt P sigui interior a la circumferència, en aquest cas d(P,C)<r.
- Que el punt P sigui un punt de la circumferència, en aquest cas d(P,C)=r.
- Que el punt P sigui exterior a la circumferència, en aquest cas d(P,C)>r .
Posició relativa entre recta i circumferència
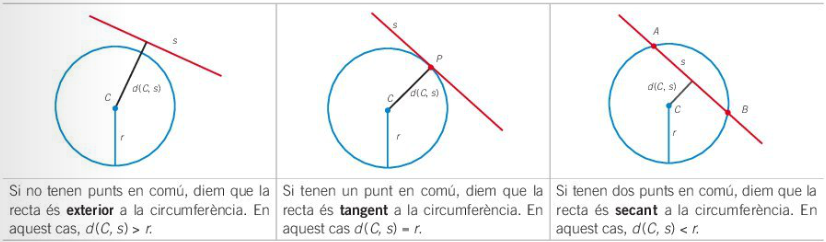
Donada una recta s i una circumferència de centre C i radi r, es poder donar aquestes tres situacions:
- Que la recta sigui exterior a la circumferència: en aquest cas recta i circumferència no tenen cap punt en comú i tenim d(s, C)>r.
- Que la recta sigui tangent a la circumferència: en aquest cas recta i circumferència es tallen en un sol punt i tenim d(s, C)=r.
- Que la recta sigui secant a la circumferència: en aquest cas recta i circumferència es tallen en dos punts i tenim d(s, C)<r.
Exercici 1: circumferència i recta
Troba l'equació de la circumferència de centre P=(-6, 1) tangent a la recta r: 3x+2y=-3
En els exercicis de geometria és important començar fent-se un dibuix esquemàtic de la situació per tal de visualitzar-la i entendre-la.
En tractar-se d'una recta tangent a la circumferència, la distància de la recta al centre serà exactament el radi.

Per tant calcularem la distància de la recta r: 3x+2y=-3 al centre de la circumferència P=(-6,1)
Recordem que la distància d'un punt P=(p1, p2 ) a una recta Ax+By+C=0 ve donat per la fórmula:
, en el nostre cas el punt és P=(-6,1) i la recta 3x+2y+3=0
Per tant p1 = -6; p2 = 1; A=3; B=2; C=3, substituïm a la fórmula de la distància i calculem.
El radi és .
Amb això ja podem obtenir l'equació de la circumferència de centre P tangent a la recta donada.
Exercici 2: circumferència i recta
a) Escriu l'equació general de la circumferència de centre (-1,5) i radi 3.
b) Donada la recta y=2x+k , troba per quin valor de k, la recta és tangent a la circumferència anterior.
Solució:
a) Comencem escrivint l'equació de tipus (x-a)²+(y-b)²= r² i després la desenvoluparem fins que ens quedi en forma general.
b) La recta serà tangent a la circumferència si la distància del centre de la circumferència a la recta és igual al radi.

Per tant calcularem la distància de la recta al centre (-1,5) i imposarem que valgui 3.
Cal recordar que la distància d'una recta r: Ax+By+C=0 al un punt P=(p1, p2
) ve donada per
En el cas que ens ocupa la recta en forma general és 2x-y+k=0 : A = 2, B=-1, C=k , p1=-1 i p2
=5 .
Ara imposem que aquesta distància valgui 3 que és el radi.
com tenim una igualtat amb un valor absolut, en traurem dues possibilitats:
Per tant tenim dues possibles k que fan que la recta donada sigui tangent a la circumferència
L'el·lipse
L'el·lipse és el lloc geomètric dels punts del pla la suma de distàncies dels quals a dos punts fixos, anomenats focus és constant.
La seva equació reduïda és de la forma
Clicant damunt la imatge accedireu a una construcció feta amb Geogebra per Lluís Riera.
Podreu comprovar de forma interactiva, que la suma de les distàncies de qualsevol punt de l'el·lipse als dos focus és constant.
- Sense tocar els punts lliscants a i b i moveu el punt P de manera que vagi recobrint tota l'el·lipse. Què observeu a la suma que es calcula a l'esquerra?
- Moveu el punt lliscant a i deixeu fix el b. Què observeu?
- Moveu el punt lliscant b i deixeu fix el a. Què observeu?
- Què passa quan a i b són iguals?
Elements de l'el·lipse
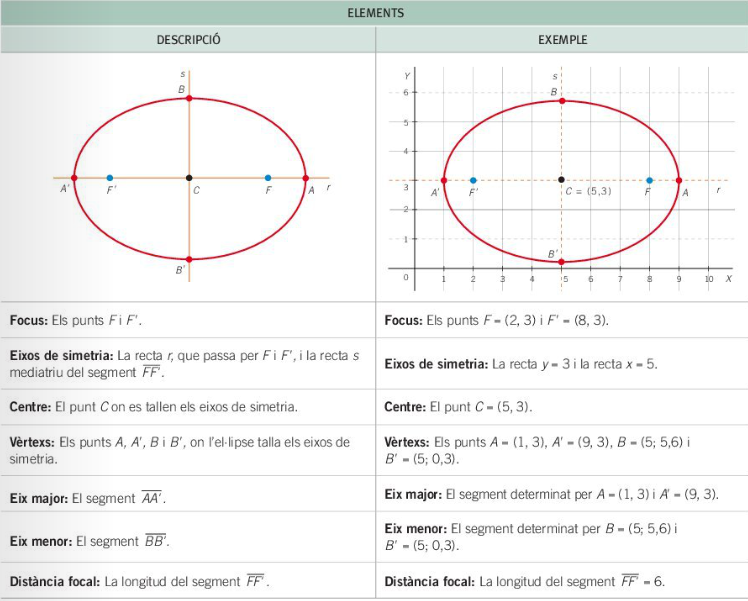
Amb la notació habitual de les el·lipses,
2c= distància focal
2a = eix major
2b = eix menor
Tenim la relació següent :
Si considerem que el centre de l'el·lipse és l'origen de coordenades i que els eixos de l'el·lipse coincideixen amb els eixos coordenats, l'equació reduïda d'una el·lipse és:
Excentricitat de l'el·lipse
És el quocient entre la semi-distancia focal i el semieix major
Aquest valor mesura si l'el·lipse és més o menys "axatada".
Aquest valor sempre està entre 0 i 1. Si e=0 tenim la circumferència, que per tant es pot pensar com un cas particular d'el·lipse.
Nota: en quest curs, només es demanarà saber distingir l'equació reduïda d'una el·lipse.
La hipèrbola
La hipèrbola és el lloc geomètric dels punts del pla, la diferència de les distància dels quals a dos punts fixos anomenats focus és constant.

L'equació reduïda de la hipèrbola centrada a l'origen és de tipus
(observa la diferència de
signe amb l'el·lipse).
La relació mètrica fonamental ve donada aplicant el teorema de Pitàgores (imatge superior)
per

Nota: en aquest curs només es demanarà saber distingir l'equació reduïda d'una hipèrbola.
La paràbola
És el lloc geomètric dels punts del pla que equidisten d'un punt fix, anomenat focus i d'una recta fixa anomenada directriu.

Elements de la paràbola

Equació reduïda de la paràbola
L'equació reduïda té forma diferent segons quin és l'eix de la paràbola OX o OY i la posició del focus.
Aquest quadre resumeix els 4 possibles casos.

Nota: en aquest curs només es demanarà saber distingir l'equació reduïda d'una paràbola.