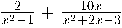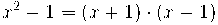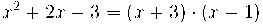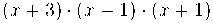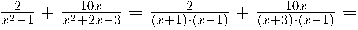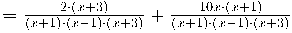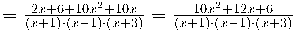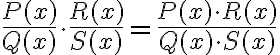Resum conceptes bàsics Tema Polinomis.
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques I (Bloc 1) ~ gener 2020 |
| Llibre: | Resum conceptes bàsics Tema Polinomis. |
| Imprès per: | Usuari convidat |
| Data: | dissabte, 4 de maig 2024, 19:52 |
Descripció
Resum conceptes bàsics del Lliurament 1: Tema polinomis.
Monomis i polinomis
El llenguatge algebraic
Les matemàtiques requereixen d'un llenguatge que ajudi a expressar-ne les idees d'una forma universal, és a dir que tothom entengui, sigui a Catalunya o al Japó. Aquesta necessitat la cobreix l'àlgebra.
És cert que a les matemàtiques apareixen molts nombres. El llenguatge numèric serveix per expressar operacions en les que només apareixen nombres.
El llenguatge algebraic utilitza lletres i nombres units pels signes de les operacions aritmètiques. Les lletres designen nombres desconeguts o genèrics, podem utilitzar qualsevol lletra tot i que les més usuals són la x, la y , la z...Aquest llenguatge ens ajuda a modelitzar situacions i problemàtiques científiques i de vegades quotidianes amb l'objectiu de facilitar-ne la resolució.
El que caldrà per plantejar problemes serà saber "traduir" el llenguatge quotidià a llenguatge algebraic. Això no sempre resulta fàcil, però cal practicar-ho perquè és essencial a l'hora de fer problemes.
Vegem-ne alguns exemples:
| Llenguatge quotidià | Llenguatge algebraic |
| si la meva edat actual és x fa tres anys tenia | |
| el doble de l'edat que tenia fa 3 anys | |
| el doble de la meva edat, menys tres | |
| la meitat d'un nombre | |
| el producte de dos nombres diferents | |
| el quadrat d'un nombre més el doble d'un altre | |
| el quadrat de la suma de dos nombres |
Monomis
Són expressions algebraiques formades pel producte d'un nombre per una o diverses lletres.
El nombre s'anomena coeficient i les lletres part literal. El grau d'un monomi serà la suma dels exponents de les lletres.
Dos monomis es diuen semblants si tenen la mateixa part literal (lletres i exponents).
Aquest tipus de llenguatge (com qualsevol altre) requereix d'unes "normes" per tal que tots ens entenguem. Enunciem les principals.
-
- No escrivim el símbol de multiplicar entre lletres ni entre lletra i nombre. Així posem 2xy² en lloc de 2·x·y²
- El coeficient d'un monomi s'escriu davant les lletres, així posem 2x en lloc de x2
- Per indicar la multiplicació d'un nombre genèric per ell mateix, fem servir les potències, així per escriure x·x·x posarem x³.
- No es posa l'exponent 1, així per exemple en lloc de posa x¹ posarem senzillament x
- Tampoc posem el coeficient 1 davant de la part literal, perquè multiplicar per 1 n o afecta, així per exemple, en lloc de posar 1xy posarem només xy.
- Quan el coeficient és -1 habitualment posem només el signe, sense l'1. Així diríem -y en lloc de -1y.
- Els nombres es poden considerar monomis de grau 0 (és com si la part literal estès elevada a 0).
| MONOMI | COEFICIENT | PART LITERAL | GRAU |
| |
|||
| y | 1 | y | 1 |
Polinomis
Li direm polinomi a la suma o resta de monomis no semblants. Cada un dels monomis que el formen li direm termes. El grau d'un polinomi és el grau més alt del termes que el formen. Al terme de grau zero li direm terme independent.
| POLINOMI | NOMBRE DE TERMES |
TERME INDEPENDENT | GRAU |
| |
3 | 1 | 4 |
| 2 | 4 | 1 | |
| 3 | 1 | 3 | 0 |
| 3 | 0 | 7 |
Operacions amb polinomis
Suma i resta de monomis
Només podrem sumar o restar monomis semblants. Per fer-ho sumarem o restarem els coeficients i deixarem la mateixa part literal
Exemples:
Suma i resta de polinomis
Per sumar dos polinomis P(x)+Q(x), sumem els seus termes semblants (és a dir del mateix grau).
Restar dos polinomis equival a sumar al primer l'oposat del segon. P(x) - Q(x) = P(x) + (-Q(x))
Exemples
Siguin
Multiplicació i divisió de monomis
Per multiplicar dos monomis es multipliquen els coeficients i es sumen els exponents (recordar les propietats de les potències).
Per dividir dos monomis es divideixen els coeficients i es resten els exponents. (Cal que el grau del dividend sigui més gran o igual al del divisor). Si la divisió dels coeficients no és exacte es deixa el resultat en forma de fracció.
Exemples :
Multiplicació i divisió de polinomis
Per multiplicar dos polinomis, cada monomi del primer multiplica a tots els termes del segon. El resultat s'ha de simplificar.Exemple:
ara multipliquem cada terme del primer polinomi per tots els termes del segon
=
finalment sumem els termes semblants per reduir l'expressió
La divisió de dos polinomis verifica sempre aquesta igualtat amb el grau del residu més petit que el grau del divisor.
| Dividend = Divisor · Quocient + Residu |
| A(x)= B(x)·Q(x)+R(x) i sempre grau (R(x))<grau (B(x)) |
Si el residu és 0 A(x)= B(x)·Q(x) diem que la divisió és exacte, també diem que A(x) és múltiple de B(x) o bé que B(x) és divisor de A(x).
Les divisions de polinomis es poden efectuar de forma molt similar a com es fan les divisions numèriques.

Ara bé, quan el divisor és de tipus amb
a un nombre qualsevol, tindrem un mètode més còmode per fer la divisió: el mètode de Ruffini que comentarem més endavant.
Igualtats notables
Per fer potències de binomis cal tenir ben present les igualtats notables.
Recordem que en tenim tres:
|
|
Aplicació en el cas de polinomis, cal simplificar al final:
caldrà aplicar la fórmula del quadrat d'una suma amb la a=x i la b=5 , llavors queda:
caldrà aplicar la fórmula del quadrat d'una resta amb a=3 i b=x , llavors queda:
caldrà aplicar la fórmula de suma per diferència amb a=4 i b=x, llavors queda
caldrà aplicar la fórmula quadrat d'una suma amb a= 3x i b=x⁵, llavors queda
Per elevar un binomi a una potència major, 3, 4, etc haurem d'aplicar la fórmula del binomi de Newton.
Regla de Ruffini
La regla de Ruffini és un procediment senzill i molt mecànic per dividir polinomis però únicament quan el divisor és de tipus x-a o x+a , amb a un nombre real.
Apliquem la regla amb un exemple:
Suposem que volem dividir 2x³ + 4x² - 3 per x - 5
Primer de tot col·locarem els coeficients del dividend començant pel de grau més gran a l'esquerra i vigilant de posar un 0 si el polinomi no és complet, per exemple ara posarem un 0 allà on tocaria posar el coeficient de grau 1, perquè no n'hi ha. A la segona fila a l'esquerra posem el terme independent del divisor canviat de signe, en aquest cas un 5 perquè anem a dividir per x-5.
Atenció! si anéssim a dividir per x + 5 posaríem -5
| 2 | 4 | 0 | -3 | |
| 5 | ||||
Completarem la fila tercera de d'esquerra a dreta seguint aquests passos
Baixem el primer coeficient del dividend (2)
Multipliquem aquest terme pel terme que hem posat a baix a l'esquerra (5) , posem el resultat a sota del següent coeficient del dividend i ho sumem.
Procedim de la mateixa manera per totes les caselles
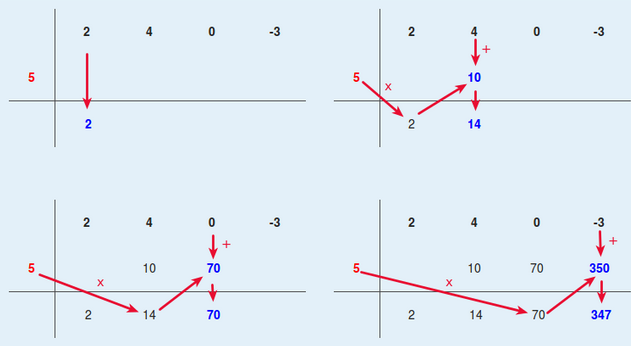
Un cop acabat el procediment ja tenim el quocient i el residu de la divisió a la fila inferior.
| 2 | 4 | 0 | -3 | |
| 5 | 10 | 70 | 350 | |
| 2 | 14 | 70 | 347 |
El terme de la dreta correspon al residu i els altres termes corresponen als coeficients del quocient (vigilar els graus)
QUOCIENT : 2x2 + 14x + 70 i el RESIDU: 347
Tenim per tant la següent igualtat: 2x³ + 4x² - 3 = ( x - 5) ·( 2x2 + 14x + 70 ) + 347
Valor numèric i Teorema del Residu
Valor numèric d'un polinomi
En el llenguatge algebraic i als polinomis en particulars, les lletres indiquen nombres qualsevol. En el moment que passem a donar-li a la o les lletres un valor concret, obtindrem un resultat numèric.
El valor numèric d'un polinomi P(x) quan x=a és el valor que s'obté en substituir la x pel valor a i fer-ne les operacions que queden indicades. Aquest valor numèric l'indicarem per P(a).
Exemples:
P(x)=x⁴ - 3x³ - 2x + 1
El valor numèric de P(x) per x=1 es calcula:
P(1)=1⁴ -3·1³ - 2·1 + 1= 1-3-2+1=2-5= -3
El valor numèric de P(x) per x= - 1 es calcula:
P(-1)=(-1)⁴ -3·(-1)³ - 2·(-1 )+ 1= 1-3·(-1)+2+1=1+3+2+1= 7
El Teorema del Residu
El valor numèric de P(x) quan x=a coincideix amb el residu que s'obté en dividir P(x) per x-a.
| P(a)= Residu de dividir P(x) per (x-a) |
Justificació: En dividir P(x) entre x-a el residu serà un nombre (recordem que el grau del residu sempre és menor que el del divisor)
Si li diem Q(x) i R al quocient i residu d'efectuar la divisió, tenim la següent igualtat
P(x)= (x-a)·Q(x)+R Si ara substituïm la x per calcular el valor numèric tenim:
P(a)=(a-a)·Q(a)+R= 0·Q(a) + R= R
Aquest teorema per tant ens proporciona una nova manera de calcular el valor numèric d'un polinomi, és a dir o bé substituïm la x pel valor que ens indiquin i operem o bé efectuem la divisió i ens quedem amb el residu, les dues coses coincidiran.
El residu el podem calcular fent la divisió clàssica o pel mètode de Ruffini.
Atenció: El residu de dividir un polinomi per (x+a) equival a P(-a).
Exemple:
Donat el polinomi P(x)=x⁴ - 3x³ - 2x + 1 de l'exemple anterior calculem P(1) utilitzant el teorema del Residu.
El teorema ens diu que P(1) és el residu de dividir P(x) entre (x-1) i això és el que farem utilitzant el mètode de Ruffini.
Col·loquem els coeficients per aplicar Ruffini i a l'esquerra posem 1 perquè anem a dividir per x-1 i apliquem l'algoritme
| 1 | -3 | 0 | -2 | 1 | |
| 1 | 1 | -2 | -2 | -4 | |
| 1 | -2 | -2 | -4 | -3 |
El terme de la dreta de la darrera fila és el residu, per tant podem afirmar P(1)= -3
Arrels d'un polinomi
Un nombre real a és arrel d'un polinomi P(x) si el valor numèric de P(x) per x=a és 0. És a dir P(a)=0.
Les arrels d'un polinomi són per tant les solucions de l'equació que s'obté en igualar a 0 el polinomi. P(x)=0.
Si a és arrel d'un polinomi podem dir tres coses equivalents:
- a és arrel de P(x)
- P(x) és múltiple de (x-a)
- (x-a) és divisor de P(x)
Si a és arrel de P(x), aquest polinomi es pot expressar com : P(x)=(x-a)·Q(x) per cert polinomi Q(x).
Com es calculen les arrels d'un polinomi?
- Polinomis de grau 1. Tenen una única arrel. Per trobar-la només cal igualar el polinomi a 0 i aïllar la x. Tenim una equació de primer grau.
Exemple: P(x)=2x+5 igualem el polinomi a 0
2x+5=0 aïllem la x----->2x=-5----->x=-5/2. Per tant l'arrel de 2x+5 és -5/2.
- Polinomis de grau 2. Poden tenir 2 arrels reals o cap. Per calcular-les resolem l'equació de segon grau que surt en igualar a 0 el polinomi.
Recordem que per trobar les solucions d'una equació de segon grau d'aquest tipus:, apliquem la fórmula
El valor que està dins de l'arrel quadrada li diem discriminant i el notem amb el símbol Δ. Segons com és aquest nombre variarà el nombre d'arrels que té el polinomi.
Si el discriminant Δ és positiu tenim dues arrels diferents
Si el discriminant Δ és 0 tenim una sola arrel però repetida
Si el discriminant Δ és negatiu el polinomi no té arrels reals
Exemple: P(x)= x² + 3x + 2
Δ=b² - 4·a·c = 3²-4·1·2=9-8=1 en ser positiu tenim 2 arrels reals.
El polinomi té les arrels -1 i -2
- Polinomis de grau superior a 2. No tenim cap mètode senzill per trobar les arrels de polinomis de grau major que dos, per tant ens limitarem a buscar-les en casos fàcils.
-Un polinomi de grau n tindrà com a màxim n arrels reals.
-Extraurem factor comú (si en té).
-Si té arrels enteres (no necessàriament en té) aquestes han de dividir el terme independent del polinomi.
Per tant farem servir el següent mecanisme:
-Buscarem els divisors del terme independent
-Provarem per Ruffini si són arrels del polinomi, és a dir si en dividir per x-a el residu dóna 0.
-Truc: si el polinomi té tots els coeficients positius segur que no té cap arrel positiva, per tant no caldria provar-les.
-Un cop trobem una arrel podem repetir el procediment amb el polinomi quocient obtingut.
- Quan arribem a un polinomi de grau 2 ja podem aplicar la fórmula explicada abans.
Exemple: Calcular les arrels del polinomi P(x)=x3 - 2x2 - 13x -10.
Com el polinomi té grau 3 sabem que com a màxim tindrà tres arrels i que si té arrels enteres aquestes han de dividir a -10.
Els divisors de -10 són : +1, -1, +2, -2, +5, -5
Provem aquests valors per Ruffini:
Comencem per +1
| 1 | -2 | -13 | -10 | |
| 1 | 1 | -1 | -14 | |
| 1 | -1 | -14 | -24 |
Com el residu no és zero, +1 no és arrel del polinomi.
Provem per -1
| 1 | -2 | -13 | -10 | |
| -1 | -1 | 3 | 10 | |
| 1 | -3 | -10 | 0 |
Com el residu és zero : -1 és arrel de P(x).
Si seguim provant pels altres valors observarem que les altres dues arrels són -2 i 5. Si ho fem per Rufini, no cal seguir amb el polinomi inicial, es pot fer a partir del quocient que hem obtingut en dividir per x+1, és a dir x²-3x-10. També podríem aplicar la fórmula de resolució de les equacions de segon grau a aquest x²-3x-10, així seria fàcil trobar les altres arrels encara que no fossin enteres.
Teorema del factor
Un polinomi P(x) té un factor (x-a) si, i només si, x=a és una arrel del polinomi.
Exemple:
(x-2) és un factor del polinomi P(x)= x³ + x² -5x -2 ja que 2 és una arrel del polinomi.
Observem que P(2)=2³ + 2² -5·2 - 2= 8 + 4 - 10 - 2= 0
per tant P(x)= (x-2)·Q(x) per trobar qui és Q(x) podem dividir el polinomi per (x-2).
Factorització d'un polinomi
Factoritzar un polinomi consisteix en escriure'l com a producte de polinomis de grau més petit. (Intentarem que sigui el grau més petit possible).
Per exemple la factorització de P(x)= x3 - 2x2 -13x -10 és (x+1)·(x+2)·(x-5).
Per realitzar la factorització d'un polinomi, tindrem en compte els mètodes següents:
-
- Treure factor comú si tots els coeficients són múltiples del mateix nombre o monomi.
-
- Identificació del polinomi amb una identitat notable
- Identificació del polinomi amb una identitat notable
-
- Buscar els divisors de la forma (x-a) aplicant Ruffini pel valor a, és a dir buscar les arrels
-
-
-
- Divisors del terme independent D(60) = {±1,±2,±3,±4,±5,±6,±10,±12,±15,±20,±30,±60}
- S'aplica Ruffini per cada divisor, i triem els divisors que donen residu "0".
- A cada divisor que compleix amb aquesta condició del residu li correspon un factor en la descomposició i podem continuar aplicant Ruffini a partir del polinomi que ens ha quedat com a quocient.
-
-
|
1 |
-8 |
11 |
32 |
-60 |
|
| 2 | 2 | -12 | -2 | 60 | |
| 1 | -6 | -1 | 30 | 0 | |
| -2 | -2 | 16 | -30 | ||
| 1 | -8 | 15 | 0 | ||
| 3 | 3 | -15 | |||
| 1 | -5 | 0 |
Per tant, es pot posar: P(x) = x4- 8x3+ 11x2 + 32x - 60= (x-2
) ·(x+2)·(x-3)·(x-5)
Observacions: Recordem que un cop arribem a un polinomi de grau dos ja tenim na fórmula per trobar les arrels i això pot resultar més ràpid en ocasions que provar per Ruffini.
Arrels d'un polinomi factoritzat
Un cop tenim el polinomi factoritzat les arrels del polinomi són els valors que anul·len cada factor, per tant caldrà igualar a zero cada factor.
Així seguint l'exemple anterior, el polinomi (x-2 ) ·(x+2)·(x-3)·(x-5)té les arrels 2, -2 , 3 i 5 ja que
x - 2 = 0------> x = 2
x + 2 = 0------>x = -2
x - 3 = 0 ------> x = 3
x - 5 = 0 ------> x = 5
Ordre o multiplicitat d'una arrel
Si un factor (x-a) es repeteix n vegades a la factorització apareixerà amb potència (x-a)n llavors direm que a és una arrel del polinomi d'ordre o multiplicitat n. És a dir té l'arrel repetida n vegades.
Exemple:
P(x)= (x+1)2(x-6) té l'arrel -1 amb multiplicitat 2 i l'arrel 6.
Fixa't per tant que el mecanisme per factoritzar un polinomi i el de trobar les arrels, són pràcticament el mateix, però la resposta a donar és diferent.
És a dir, si ens demanen trobar la factorització del polinomi P(x) = x4- 8x3+ 11x2 + 32x - 60 hauríem de dir P(x)= (x-2 ) ·(x+2)·(x-3)·(x-5).
Si ens demanen quines són les arrels de P(x) = x4- 8x3+ 11x2 + 32x - 60 la resposta hauria de ser: 2, -2 , 3 i 5.
Exercici
Donat el polinomi factoritza'l al màxim, és a dir escriu-lo com a producte de factors de grau 1. Aprofita després la factorització obtinguda per trobar-ne les tres arrels.
Ho farem de dues maneres:
Forma 1
Com aquest polinomi no té factors comuns ni tampoc es tracta de cap igualtat notable començarem buscant factors de tipus (x-a) aplicant Ruffini amb el valor a. (això equival a trobar les arrels).
És a dir dividirem el polinomi per (x-a) si el residu dóna 0, voldrà dir que té el factor (x-a), si el residu no dóna 0, en buscarem un altre.
Comencem provant els valors enters que han de ser divisors del terme independent del polinomi.
Com en aquest cas és un -2 els seus divisors són {+1, -1, +2, -2} aquestes són les úniques possibles arrels enteres del polinomi.
Comencem provant per 1
|
3 |
4 |
-5 |
-2 |
|
| 1 | 3 | 7 | 2 | |
| 3 | 7 | 2 | 0 |
Com hem obtingut residu 0, vol dir que (x-1) és un factor i per tant de moment ja sabem que el polinomi P(x) es pots escriure així:
observem que els coeficients del segon factor es corresponen amb els que hem obtingut com
a quocient del Ruffini.
Cal continuar perquè encara tenim un factor de grau dos. Seguirem aplicant Ruffini al segon factor. Provem pel valor -2 (al quadern pots provar els altres i veuràs que no donen residu 0)
|
3 |
7 |
2 |
|
| -2 | -6 | -2 | |
| 3 | 1 | 0 |
Tenim un altre factor i de fet ja estem perquè en el quocient de Ruffini ens queda el tercer factor que busquem.
Un cop tenim els tres factors de grau 1, aprofitem la factorització per trobar les tres arrels que seran els valors que anulen cadascun dels tres factors.
Forma 2
La primera part la faríem exactament igual, és a dir buscaríem un primer factor de tipus (x-a) i provaríem pels divisors de -2 concretament comencem per 1
|
3 |
4 |
-5 |
-2 |
|
| 1 | 3 | 7 | 2 | |
| 3 | 7 | 2 | 0 |
Com hem obtingut residu 0, vol dir que (x-1) és un factor i per tant de moment ja sabem que el polinomi P(x) es pots escriure així:
Arribat aquest punt en lloc de continuar fent Ruffini podem treballar directament amb el factor de grau 2 que hem obtingut. Li buscarem les arrels i cada arrel ens donarà un factor de tipus (x-arrel)
Apliquem la fórmula de resolució de les equacions de segon grau per a resoldre . Per
tant a=3 , b= 7 i c=2
I ara cal vigilar.
Tenim l' arrel -2 , per tant tenim el factor
Com també tenim l'arrel , tindrem el factor
Finalment escrivim el polinomi factoritzat així
Observeu que en aquest cas ha calgut posar un 3 davant perquè el polinomi inicial té un 3 en el coeficient de grau màxim.
Fixeu-vos també que que és el factor que
ens havia sortit en el primer mètode, qualsevol dels dos factors és correcte, perquè té grau 1.
Les arrels ja les tenim, .
Exercici
Donat el polinomi ,
troba el valor de k per tal que el polinomi tingui l'arrel -5. Pel valor obtingut calcula quines serien les altres arrels.
Resolució:
Aplicarem Ruffini amb el valor -5 i imposarem que el residu sigui 0 per tal que -5 sigui arrel del polinomi.
Ara imposem que el residu obtingut sigui 0.
De moment sabem que per k= -1 el polinomi té l'arrel -5, i amb el Ruffini que hem fet podem afirmar que el polinomi factoritza de la següent manera:
Busquem les dues arrels del polinomi de grau 2 (es podria fer per Ruffini, però ho farem aplicant la fórmula de resolució de les equacions de grau 2).
m.c.m i m.c.d de polinomis
Tal com fem amb els nombres, amb els polinomis també en podem calcular el M.C.D i M.C.M.
Això ens serà útil per exemple per fer operacions amb fraccions algebraiques.
El M.C.D (màxim comú divisor) de diversos polinomis és el divisor comú de major grau.
Per calcular-lo:
- Factoritzem els polinomis.
- Escollim els factors comuns elevats al menor exponent.
- Fem el producte d'aquests factors.
El M.C.M (mínim comú múltiple) de diversos polinomis és el múltiple de grau més petit comú a tots ells.
Per calcular-lo:
- Factoritzem els polinomis.
- Agafem tots els factors tant els comuns com els no comuns elevats a l'exponent més gran.
- Fem el producte d'aquests factors.
Calculem el M.C.D i el M.C.M dels següents polinomis:
P(x)= x³ + x² - x -1
Q(x)= x³ + 3x² - x - 3
- Factoritzem aquests polinomis amb els mètodes explicats anteriorment
P(x) = (x+1)²·(x-1)
Q(x)= (x+1)·(x-1)(x+3)
- Per calcular el M.C.D escollim els factors repetits elevats a l'exponent més petit i els multipliquem. En aquest cas el factor (x-1) és a les dues expressions i també (x+1) i l'exponent més petit de tots dos és 1, per tant el M.C.D serà:
(x-1)·(x+1)= x² - 1 - Per calcular el M.C.M agafem tots els factors comuns i no comuns elevats a l'exponent més gran i els multipliquem. En aquest cas per tant el M.C.M serà:
(x-1)·(x+1)²·(x+3)= x⁴ +4x³ +2x² -4x - 3
Fraccions algebraiques
Una fracció algebraica és el quocient de dos polinomis P(x) i Q(x), amb Q(x)≠0
Les operacions amb fraccions algebraiques s'assemblen a les operacions amb fraccions numèriques.
Fraccions equivalents
de forma anàloga al que passa amb fraccions numèriques.
Exemple:
Son equivalents les dues fraccions algebraiques següents?
Si apliquem la definició de fraccions algebraiques equivalents caldria comprovar que :
Ho comprovem:
Per tant són equivalents.
Tot i això hagués estat més fàcil simplificar la fracció algebraica de la dreta i comprovar que donava exactament la fracció de l'esquerra.
Simplificació de fraccions
Per simplificar una fracció algebraica cal dividir numerador i denominador pel mateix factor, fins obtenir una fracció irreductible.
Prèviament cal factoritzar cada polinomi i simplificar els factors comuns.
Exemple:
Simplifica la fracció algebraica:
Cal factoritzar els polinomis :
i queda :
Observem que podem dividir numerador i denominador per (x-2)
per tant la fracció simplificada seria:
Suma de fraccions algebraiques
Per sumar o restar fraccions algebraiques, cal que tinguin un mateix denominador. Cal trobar el mcm dels denominadors. El procediment és igual que en sumar i restar fraccions numèriques:
- Es calcula el m.c.m dels denominadors (prèviament cal factoritzar-los)
- Es busquen les fraccions equivalents a les inicials amb denominador el m.c.m buscat.
- Es sumen o resten els numeradors
- Es simplifica al màxim la fracció resultant.
Exemple
Exemple de suma de fraccions algebraiques:
Ara ja tenen el mateix denominador, només cal sumar els numeradors:
Producte i divisió de fraccions algebraiques
- La multiplicació de fraccions algebraiques és igual que les multiplicacions de fraccions numèriques:
Però s'ha d'evitar fer efectiva la multiplicació. És millor provar de simplificar al màxim la fracció resultant
- La divisió de fraccions algebraiques és igual que les multiplicacions de fraccions numèriques: