Resum dels conceptes bàsics Tema Reals
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques I (Bloc 1) ~ gener 2020 |
| Llibre: | Resum dels conceptes bàsics Tema Reals |
| Imprès per: | Usuari convidat |
| Data: | dijous, 9 de maig 2024, 03:33 |
Descripció
Resum dels conceptes bàsics del Lliurament 1: tema nombres reals.
Els nombres reals
Avui dia el concepte de nombre el tenim força clar, el trobem en el nostre dia a dia en infinitat de situacions: quan diem la nostra edat, el pes, els límits de la velocitat, el preu que paguem, ....etc. També sabem que n'hi ha de molts tipus: positius, negatius, enters, decimals, amb pocs decimals, amb infinits decimals...Al llarg de la història la noció de nombre va anar sorgint en diferents etapes i a mida que sorgia la seva necessitat. Els primers nombres, que s'idearen per la necessitat de comptar objectes, es van anar ampliant amb el concepte de negatiu, el zero, les parts....
Tot això ha portat avui dia a classificar els nombres com mostra la imatge inferior.

És important saber distingir cada tipus de nombre i saber treballar i operar amb ells correctament, tant amb llapis i paper com amb calculadora.
Cal que vigilar a l'hora de donar els resultats obtinguts amb la calculadora. Les calculadores utilitzen la notació anglosaxona, de manera que escriuen , com a punt de milers i escriuen · per separar la part entera de la decimal, per tant és molt important no confondre's i expressar-ho bé.
Tal com es veu en aquest esquema, la primera classificació dels nombres reals és en racionals i irracionals. Veiem que vol dir cada cosa.
Els nombres racionals (Q)
Són tots aquells que es poden expressar mitjançant una fraccióEls nombres enters i les fraccions ja els heu treballat força al llarg dels anteriors estudis, de tota manera en els primers capítols d'aquest llibre se'n recordem les normes bàsiques que cal que interioritzeu i utilitzeu amb correcció al llarg de tots els lliuraments.
Els nombres irracionals (I)
Els nombres irracionals no es poden expressar com una fracció. La seva expressió decimal té infinites xifres que no segueixen cap periodicitat, cap regularitat. També hi ha infinits nombres irracionals com:Segur que d'irracionals en coneixes molts. Mira't aquest vídeo del matemàtic Adrian Paenza on s'explica de forma molt il·lustrativa una situació quotidiana en la què ens apareix el nombre
En considerar l'expressió decimal dels nombres irracionals (i també dels racionals que tenen molts decimals) cal treballar amb aproximacions davant de la impossibilitat de tractar infinites xifres. Això suposa que en fer operacions anem acumulant error. Per això és recomanable treballar amb l'expressió real sempre que sigui possible i serà important dominar el càlcul amb radicals (que s'explica al capítol 4 d'aquest mateix llibre) i el càlcul amb expressions algèbriques.
Els nombres enters
Els nombres enters són un cas particular de nombre racional amb denominador 1. Hi ha enters positius, que coneixem com a nombres naturals i representem amb la lletra Es poden representar en una recta: en mig el 0, els positius a la dreta i els negatius a l'esquerra.
Saber operar amb nombres enters serà bàsic al llarg de tot el curs i és un dels principals errors que es cometen. Saber fer un bon ús de la calculadora és molt important com també conèixer el mecanisme de les diferents operacions. En aquest capítol en recordem els conceptes i les propietats bàsiques que cal saber per evitar errors comuns.
Valor absolut d'un nombre enter
El valor absolut d'un nombre enter és el mateix nombre si és positiu i el valor oposat si és negatiu. Es representa amb el nombre entre dues barres verticals |n|.
Observació: El valor absolut d'un nombre és la distància del nombre al zero i que per això sempre ha de ser positiu.
Exemples:
Els parèntesis
A l'hora d'operar ens trobem moltes vegades amb nombres amb parèntesis. Per treballar-hi és còmode eliminar els parèntesis que no siguin necessaris
seguint aquesta regla:- Un signe negatiu davant d'un parèntesi canvia el signe del que hi ha a l'interior.
- Un signe positiu davant d'un parèntesis no canvia el signe de dins
Recordem les propietats de les principals operacions amb enters.
Suma i resta d'enters
Suma d'enters amb el mateix signe
- Sumem els valors absoluts dels nombres.
- Posem al resultat el mateix signe dels nombres.
Exemples:
Suma d'enters amb signe diferent
- Restem els valors absoluts del nombres.
- Posem al resultat el signe del nombre que té major valor absolut.
Exemples:
Aquesta imatge il·lustra això que hem dit, és a dir si els dos són del mateix signe la suma del mateix signe i si són de signes diferents "guanya" el signe del més gran.
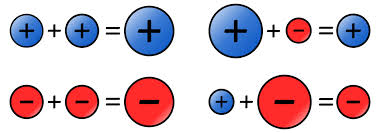
Resta de dos nombres enters
Restar dos nombres enters consisteix en sumar al primer, el segon canviat de signe (l'oposat).Exemples:
Suma i resta de més de dos nombres
Tot i que es pot fer de diverses formes, és aconsellable si hem de fer diverses sumes i restes seguides primer sumar entre ells els nombres del mateix signe i finalment fer la darrera operació que en resulta.
Exemple:
de moment eliminem els parèntesis vigilant els signes
ara sumem d'una banda tots els positius i per l'altra tots els negatius
finalment realitzem la darrera operació que queda
Multiplicació i divisió de nombres enters
Quan multipliquem o dividim nombres amb signes hem de tenir en compte la següent norma:
Regla dels signes
- Multipliquem o dividim els seus valors absoluts
- Posem el signe tenint en compte la següent llei:

Ho podem resumir així:
Exemples:
(+5) · (+9) = 5·9= +45
(–5) · (+9) = (–5) · 9 = –45
(+45): (-9)= 45 : (-9) =-5
(-45) : (-9)= +5
(-4) · (-2) · (+5)= (+8) ·(+5)= +40
(-4) · (-1) · (-2) · (+6) =(+4) · (-12)= -48
Algunes observacions a tenir en compte:
- Habitualment per expressar la multiplicació posarem un punt com a símbol (així 3·4=3x4)
- Si cal fer diverses divisions i multiplicacions, aquestes es faran d'esquerra a dreta.
(-16):(+2)·(-5)=(-8)·(-5)=+40
- Molt de compte en fer les sumes i restes d'enters, és habitual cometre l'error d'aplicar la llei dels signes de la multiplicació!!
Potències
Una potència és la multiplicació d'un nombre per si mateix moltes vegades seguides.
Així per exemples: 2·2·2·2·2 ho escrivim en forma de potència com 25 . És a dir, escrivim el nombre que multipliquem un sol cop i posem a dalt, a la dreta el nombre de vegades que el multipliquem.
Potències amb exponent positiu
La potència de dos nombres enters (-3)4 és el producte del primer nombre (base) per si mateix tants cops com indica el segon nombre (exponent).
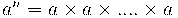 |
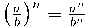
|
Tenint en compte que una potència no és més que una forma més curta d'expressar multiplicacions caldrà tenir en compte la llei dels signes de la multiplicació explicada abans.
Ho podríem resumir així:
- Si la base és positiva la potència sempre és positiva: (positiu)exponent=positiu
- Si la base és negativa i l'exponent parell el resultat és positiu: (negatiu)parell=positiu
- Si la base és negativa i l'exponent senar el resultat és negatiu: (negatiu)senar=negatiu
Exemples:
Potències amb exponent negatiu
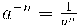 |
Exemples:
Propietats de les potències
És molt important pels càlculs de tot el curs que domineu les propietats de les potències:
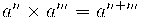 |
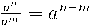 |
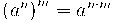 |
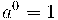 |
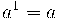 |
Exemples:
Per fer potències amb la calculadora científica podeu utilitzar la tecla ^ o
![]() segons el model que tingueu (mireu el manual de la vostra calculadora).
segons el model que tingueu (mireu el manual de la vostra calculadora).
Per escriure potències a la pantalla d'edició del campus, podeu consultar: Escriure super-índex i sub-índex a la pantalla d'edició
Amb quin ordre cal fer les operacions quan en tenim moltes?
Quan tenim diferents operacions seguides, l'ordre en què heu de realitzar-les és:
-
- Fem les operacions de dins dels parèntesis i claudàtors. (Si n'hi ha un dins d'un altre és comença pel de l'interior)
- Fem les potències i arrels
- Fem els productes i divisions (d'esquerra a dreta)
- Fem les sumes i restes (d'esquerra a dreta)
Exemples:
Fraccions
Calcular amb fraccions et serà imprescindible al llarg del curs, per això, tot i que és un tema que has treballat en molts cursos anteriors te'n recordem les regles bàsiques i et recomanem que si et costa practiquis pel teu compte. Avui dia, motes calculadores científiques treballen amb l'expressió natural de les fraccions. Si és el cas de la teva, aprofita-ho i consulta'n en manual.
Reduir fraccions a comú denominador
Consisteix a trobar fraccions equivalents a les inicials però totes amb el mateix denominador.
-
- El denominador comú serà el m.c.m dels denominadors inicials
- Per trobar els numeradors es divideix el m.c.m pel denominador i es multiplica pel numerador.
Exemple:
Volem reduir a comú denominador i
-
- Calculem el m.c.m(12,8)
12=3·2²·1
8=2³·1
Recordem factors comuns i no comuns elevats a l'exponent més gran, per tant m.c.m(12,8)=3·2³=3·8=24. El denominador comú és 24 - Ara calculem els numeradors:
dividim 24:12=2---->multipliquem pel numerador---->2·7=14---->
dividim 24:8=3---->multipliquem pel numerador---->3·3=9---->
Ja tenim les dues fraccions equivalents a les primeres però amb denominador comúi
- Calculem el m.c.m(12,8)
Fraccions irreductibles
Una fracció és irreductible si el numerador i denominador són primers entre ells, és a dir si no tenen divisors comuns llevat de l'1.
En fer operacions amb fraccions és molt habitual que es demani el resultat en forma de fracció irreductible, en aquest cas haurem de reduir o simplificar la fracció resultant.
Reduir i simplificar una fracció consisteix en trobar una fracció equivalent a la inicial dividint el numerador i denominador per un divisor comú a tots dos, això es pot fer diversos cops fins arribar a la fracció irreductible. Si dividim el numerador i denominador pel m.c.d de tots dos arribem en un sol pas a la fracció irreductible.
Exemples

Operacions amb fraccions
Suma i resta
- Si les fraccions tenen el mateix denominador la suma/resta és una fracció amb el mateix denominador i el numerador suma /resta dels numeradors
- Si tenen denominador diferent, primer cal reduir-les a comú denominador i després procedir com en el cas anterior.
- En tots dos casos, cal simplificar el resultat final de l'operació.
Exemples:
Multiplicació
La multiplicació de dues o més fraccions és una nova fracció que té per numerador el producte dels numeradors i per denominador el producte de denominadors. Cal simplificar el resultat.
![]()
Exemples
Divisió
Dividir dues fraccions és el mateix que multiplicar la primera fracció per la inversa de la segona. La manera més ràpida de dividir dues fraccions és multiplicant en creu els seus elements i simplificant el resultat final.
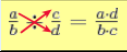
Atenció: la divisió de fraccions també es pot expressar així:
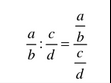
Exemples
Operacions combinades amb fraccions
-
- Pot ser convenient simplificar les fraccions prèviament i/o simplificar-les a cada pas.
- Parèntesis i claudàtors (si n'hi ha més d'un es comença pel més intern)
- Potències i arrels
- Multiplicacions i divisions (d'esquerra a dreta)
- Sumes i restes
- Es simplifica el resultat final.
Exemples
Radicals
Què són els radicals?
La radicació és l'operació inversa de la potència.Així tenim que :
A la a li diem radicand, la n l'anomenem índex i la b és l'arrel
Si la a és negativa i l'índex és parell, l'arrel no existeix.
Si la a és negativa i l'índex és senar, l'arrel pren un sol valor negatiu.
Si la a és positiva i l'índex parell , l'arrel pren dos valors oposats.
Si la a és positiva i l'índex és senar, l'arrel pren un sol valor positiu.
Exemples:
no existeix perquè cap nombre elevat a la quarta dona negatiu
En general quan l'índex és 2, aquest no es sol escriure i diem que tenim una arrel quadrada.
Radicals expressats com a potències fraccionaries
Els radicals es poden expressar com a potències d'exponents fraccionaris. Així tenim que:
Exemple:
Per calcular el valor dels radicals amb la calculadora podeu utilitzar les tecles
![]() o bé
o bé
![]() segons els models
segons els models
Algunes arrels són nombres enters, per exemple és
o
és 5. Però en molts casos l'expressió decimal d'alguns radicals té infinites xifres decimals sense cap regularitat (tot i que la calculadora només ens doni el nombre finit de dígits que hi caben a la pantalla), és a dir es tracta de nombres irracionals.
Per evitar acumular errors en aproximar aquests valors és bo dominar les propietats del càlcul amb radicals i utilitzar-les en els problemes i exercicis que sigui necessari. Si escriviu les arrels com a potències amb exponent fraccionari, podeu aprofitar les propietats de les potències i el càlcul amb fraccions per operar amb radicals si us és còmode.
Propietats dels radicals
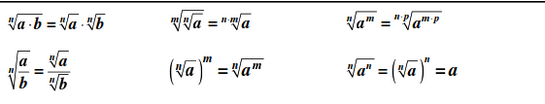
Atenció:
![]()
Per tant vigileu típics errors com el que segueix:
Seria això correcte?
Naturalment NO, doncs en el primer pas s'ha comès una errada greu.
El desenvolupament correcte seria :
.
Factors i radicals
Introduir factors dins d'un radical
Si volem introduir un factor dins del radical cal fer-ho elevant-lo a l'índex del radical
![b \sqrt[n]{a}=\sqrt[n]{a\cdot{b}^{n}} b \sqrt[n]{a}=\sqrt[n]{a\cdot{b}^{n}}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/ebcae024beb809a8fea3da1baf421021.gif) |
Així per exemple podem fer:
Extreure factors d'un radical
Podem fer el pas a l'invers per extreure factors fora del radical. Cal però que l'exponent del factor sigui més gran que l'índex del radical.
En aquest cas, dividirem l'exponent del factor entre l'índex del radical, el quocient (q) ens indica quants factors extraiem i el residu (r) quina potència queda dins del radical.
![\sqrt[n]{{a}^{m}}={a}^{q}\cdot\sqrt[n]{{a}^{r}} \sqrt[n]{{a}^{m}}={a}^{q}\cdot\sqrt[n]{{a}^{r}}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/c609e868f35d357a16c0e0327fba2e46.gif) |
Exemples:
Si volem extreure tots els factors possibles de ![\sqrt[5]{{5}^{13}} \sqrt[5]{{5}^{13}}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/54ecd43ce6d1c7356299a4be3ccff558.gif) farem el següent:
farem el següent:

Si el radicand no està factoritzat caldrà fer-ho prèviament.
Exemple
Volem extreure tots els factors possibles d'aquest radical 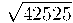
- Factoritzem 42525=35·52·7
- Ara ja podem treure els factors
Simplificar
La simplificació de radicals: consisteix en escriure un radical equivalent amb l'índex més petit ( a ser possible). Serà còmode escriure el radical en forma de potència fraccionaria i simplificar la fracció.
Exemple:
Reducció a índex comú i operacions
Reducció a índex comú
Es tracta de trobar radicals equivalents als inicials amb l'índex comú, aquest índex serà el m.c.m dels inicials. Utilitzarem la propietat , és recomanable posar els radicals en forma de potència amb exponent
fraccionari i reduir les fraccions a comú denominador.
Exemple:
mcm(4,14)=28
Suma i resta de radicals
Només es poden sumar i restar radicals semblants, és a dir si tenen el mateix índex i el mateix radicand. Cal primer treure factors fora del radical.Exemple:
Producte i divisió de radicals
Cal que tinguin el mateix índex. Si no els tenen els reduïm primer a índex comú.
Exemple:
Podem extreure factors de l'arrel i queda
Igualtats notables amb radicals
Aquestes igualtats les seguirem treballant en propers lliuraments, però és important que ara ja es comencin a utilitzar i a tenir clars.
|
|
Exemples:
Racionalització
L'objectiu de racionalitzar és eliminar els radicals dels denominadors. Caldrà fer servir diferents estratègies segons com siguin els denominadors. A continuació s'expliquen els dos casos més usuals.
S'ha de buscar el terme apropiat per fer la racionalització.
Tot i que hi ha molts casos possibles, anem a exemplificar els més comuns.
Si el denominador només té un radical
amb
Observa que es multiplica el numerador i el denominador pel mateix factor (d'aquesta manera la fracció no queda modificada).
En el cas particular que l'arrel sigui quadrada l'expressió seria:
Exemple:
Si el denominador és un binomi i almenys un dels dos termes és un radical amb índex 2
S'ha de multiplicar per l'expressió conjugada, és a dir canviant el signe del binomi (si era + posarem - i al revès). L'objectiu és que al denominador arribem a la igualtat notable suma per diferència i d'aquesta manera s'eliminin les arrels.
En el cas que només un dels dos termes del binomi tingui arrel, es procedeix de la mateixa manera.
Exemple:
Intervals
Recta real
Els nombres reals es poden representar en una recta que anomenen recta real. A cada punt de la recta li correspon un únic nombre real i a l'inrevés. Els nombres reals segueixen una ordenació de manera que quan més petit és un nombre, més a l'esquerra de la recta està representat.
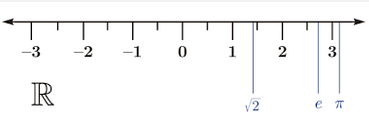
Intervals
Un interval és un conjunt de nombres reals que es representen sobre la recta com un segment o una semirecta ( en el cas d'intervals infinits).
Serà important que dominis aquesta nomenclatura matemàtica doncs la faràs servir en diversos temes de la matèria.
Qualsevol interval té infinits punts i per indicar si els extrems pertanyen o no al conjunt fem servir símbols diferents. Així farem servir el parèntesis ( , ) si volem indicar que els extrems no pertanyen al conjunt i farem servir el claudàtor [ , ] per indicar que sí que hi pertanyen.
Observa la notació en què s'expressen els intervals infinits i que el dibuix és una semirecta que indica amb una fletxa que no s'acaba.
Tipus d'intervals:


Com veus hi ha diverses maneres d'expressar el mateix conjunt de punts: per definició, amb un interval i amb un dibuix sobre la recta real.
Per exemple, com indicaríem matemàticament el conjunt de nombres més grans que tres i més petits o iguals a 5?
- Per definició amb notació matemàtica:
- En forma d'interval
(fixa't el 3 no pertany al conjunt, per això hem posat parèntesis i el 5 sí i per això hem posat claudàtor)
- Dibuixant el segment sobre la recta
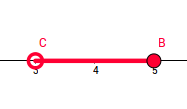 (observa el dibuix dels punts extrems en funció que formin part o no del conjunt circumferència en cas que no pertanyi i cercle ple en cas que sí hi pertanyi)
(observa el dibuix dels punts extrems en funció que formin part o no del conjunt circumferència en cas que no pertanyi i cercle ple en cas que sí hi pertanyi)
Si vols practicar amb els intervals, clica damunt la següent imatge i accediràs a un applet fet amb Geogebra per Luís Castillo i Antonio Omatos que et permetrà movent els punts lliscants veure el dibuix i les expressions de diferents intervals finits.
Notació científica
En molts contextos reals ens trobem amb la necessitat d'escriure nombres molt grans o molt petits. L'escriptura d'aquests nombres suposa escriure moltes xifres amb les molèsties que això comporta, és per això que per fer més còmoda aquesta escriptura tenim la notació científica.
Un nombre escrit en notació científica té aquesta forma: C·10n
on C és un nombre amb una sola xifra entera (entre 1 i 9) i n. Si la n és positiva el nombre és molt gran i si la n és negativa el nombre és molt petit.
Així per exemple escrivim:
- La massa del Sol és 2·1030 kg en lloc de 2000000000000000000000000000000 kg.
- La càrrega d'un electró és 1,6·10-19 en lloc de 0,00000000000000000016
- El radi de la Terra mesura aproximadament 6,37·106 m en lloc de 6370000 m
És important treballar bé amb els nombres en notació científica amb i sense calculadora.
En moltes calculadores per escriure les potències de 10 disposes de la tecla EXP , així per exemple per escriure 2,5·1012 faríem: 2,5 EXP 12
Aproximacions i errors
Aproximacions i estimacions
Per treballar amb nombres amb moltes xifres decimals, es fan aproximacions. Aquestes aproximacions poden ser per excés si l'aproximació és més gran que el valor exacte o per defecte si l'aproximació és més petita que el valor exacte.
Utilitzem dos mecanismes bàsics d'aproximació:-
- TRUNCAMENT: prenem les xifres decimals que necessitem i eliminem la resta.
- ARRODONIMENT: prenem les xifres decimals que necessitem i eliminem la resta modificant, si cal, la darrera xifra decimal seguint aquesta regla:
Si la primera xifra que eliminem és inferior a 5, deixem igual les xifres anteriors.
Si la primera xifra que eliminem és igual a superior a 5, sumem 1 a la xifra anterior.
Exemples
| Valor exacte | Ordre | Truncament | Arrodoniment |
| 234,5627 | centèsims | 234,56 | 234,56 |
| 234,5627 | mil·lèsims | 234,562 | 234,563 |
| 0,95555555 | dècims | 0,9 | 1 |
| π=3,141592... | mil·lèsims | 3,141 | 3,142 |
De la mateixa manera en mesurar magnituds se'n fa una estimació i aquestes comporten un error experimental degut a la manca de precisió que es comet.
Quan es fan aproximacions o estimacions de quantitats interessa conèixer-ne l'error comès o almenys acotar-lo.
Errors
En aproximar un nombre cometem un error, ja que no estem considerant el valor exacte. És bo conèixer o almenys acotar l'error que estem comentem per valorar la precisió dels nostres càlculs.
L'error absolut Eaés la diferència en valor absolut entre el valor exacte i l'aproximació.
L'error relatiu Er és el quocient entre l'error absolut i el valor absolut del valor exacte. Aquest ens indica quin és l'error comès per unitat (habitualment es dóna en %) i ens serveix per comparar diverses aproximacions, per
saber quina és més precisa.
Tanmateix, dels nombres amb infinites xifres no en coneixem el valor exacte i per això no podem calcular-ne l'error relatiu, sinó només una fita, és a dir podrem dir que l'error comés és menor que un cert valor. El càlcul d'aquesta fita no és únic, una forma de fer-ho és aquesta:
Fita de l'error absolut <|Aproximació per excés- Aproximació per defecte|

Xifres significatives
Són els dígits que es coneixen amb precisió més un darrer dígit que s'ha aproximat o estimat. En contextos científics és important treballar amb el nombre de xifres significatives que es demanin.
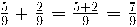
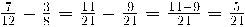
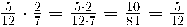
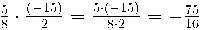
![2 \sqrt[4]{5}=\sqrt[4]{5\cdot{2}^{4}}=\sqrt[4]{80} 2 \sqrt[4]{5}=\sqrt[4]{5\cdot{2}^{4}}=\sqrt[4]{80}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/e1285a001ae328b1f7019d89ec6d40d3.gif)
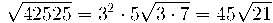
![\sqrt[12]{{5}^{8}}=5^{ \frac{8}{12} }=5^{ \frac{2}{3} }= \sqrt[3]{5^{2}} \sqrt[12]{{5}^{8}}=5^{ \frac{8}{12} }=5^{ \frac{2}{3} }= \sqrt[3]{5^{2}}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/726929bec26a63d12e8f67defc6238d9.gif)
![\sqrt[4]{2^5} \sqrt[4]{2^5}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/572d3b04fc119729a39a48f1c6297a5f.gif)
![\sqrt[14]{3^4} \sqrt[14]{3^4}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/d00aaa25250099aa43e2c63cf3d426e4.gif)
![\sqrt[4]{2^5}= 2^{\frac{5}{4}}=2^{\frac{35}{28}}=\sqrt[28]{2^{35}} \sqrt[4]{2^5}= 2^{\frac{5}{4}}=2^{\frac{35}{28}}=\sqrt[28]{2^{35}}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/6ae52010d0cc58013178a737dd2b6d3c.gif)
![\sqrt[14]{3^4}=3^{\frac{4}{14}}=3^{\frac{8}{28}}= \sqrt[28]{3^8} \sqrt[14]{3^4}=3^{\frac{4}{14}}=3^{\frac{8}{28}}= \sqrt[28]{3^8}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/bec8d12edb77fa53f02c0f9b35ba26c0.gif)
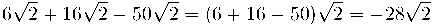
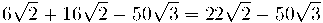
![6 \sqrt{2} \cdot \sqrt[5]{8} =6\sqrt[10]{2^5} \cdot \sqrt[10]{8^2}=6 \sqrt[10]{2^5} \cdot \sqrt[10]{2^{6}}=6\sqrt[10]{2^{11}} 6 \sqrt{2} \cdot \sqrt[5]{8} =6\sqrt[10]{2^5} \cdot \sqrt[10]{8^2}=6 \sqrt[10]{2^5} \cdot \sqrt[10]{2^{6}}=6\sqrt[10]{2^{11}}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/9754d7aacfb667c7e494118c6bbdc11a.gif)
![6\cdot 2\sqrt[10]{2}=12\sqrt[10]{2} 6\cdot 2\sqrt[10]{2}=12\sqrt[10]{2}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/1ed9fae11801b4783d626976c4c17509.gif)
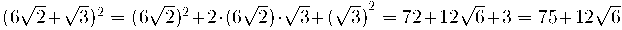
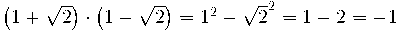
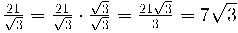
![\frac{20}{ \sqrt[4]{2}}= \frac{20}{ \sqrt[4]{2}} \cdot {\frac{ \sqrt[4]{2^3}}{ \sqrt[4]{2^3}}}= \frac{20 \sqrt[4]{2^3}}{ \sqrt[4]{2^4}}= \frac{20 \sqrt[4]{2^3}}{2}=10 \sqrt[4]{2^3} \frac{20}{ \sqrt[4]{2}}= \frac{20}{ \sqrt[4]{2}} \cdot {\frac{ \sqrt[4]{2^3}}{ \sqrt[4]{2^3}}}= \frac{20 \sqrt[4]{2^3}}{ \sqrt[4]{2^4}}= \frac{20 \sqrt[4]{2^3}}{2}=10 \sqrt[4]{2^3}](https://educaciodigital.cat/ioc-batx/moodle/filter/tex/pix.php/992cbb8e88571e412155ae9b5bac285b.gif)
