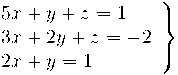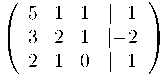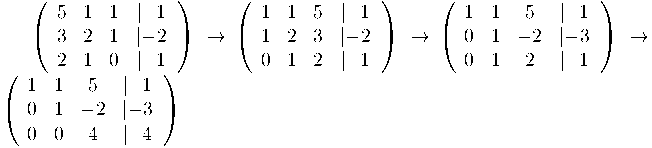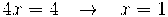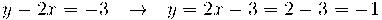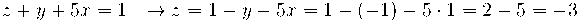Resum Sistemes d'equacions
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques aplicades a les Ciències socials (autoformació IOC) |
| Llibre: | Resum Sistemes d'equacions |
| Imprès per: | Usuari convidat |
| Data: | dijous, 9 de maig 2024, 03:14 |
Descripció
Dubtes freqüents sistemes d'equacions
Taula de continguts
- 1. Tipus de sistemes
- 2. Recordatori dels sistemes de dues equacions.
- 3. Notació matricial
- 4. Transformacions elementals
- 5. Mètode de Gauss
- 6. Classificació d'un sistema d'equacions: Teorema de Rouché-Frobenius
- 7. Classificació d'un sistema depenent d'un paràmetre
- 8. Canvi de files o columnes en la matriu associada a un sistema d'equacions.
- 9. Solucions d'un sistema compatible indeterminat
- 10. Determinats d'ordre 2 o 3
- 11. Matriu inversa
- 12. Plantejament i resolució problemes
1. Tipus de sistemes
Sistemes d'equacions lineals.
Són sistemes del tipus:
on les aij són nombres i diem que són els coeficients del sistema,
les bi són els termes independents del sistema,
les xi són les variables o incògnites del sistema
El que hem escrit és un sistema general de m equacions i n incògnites.
Una solució (s1, s2, ... sn) és solució del sistema si verifica simultàniament totes les equacions.
Fins ara hem treballat amb els sistemes de 2 equacions i 2 incògnites.
En aquest lliurament principalment treballarem amb sistemes de 3 equacions i 3 incògnites que designarem, de manera més pràctica, per x, y i z.
Exemples:
és un sistema de 3 equacions i 3 incògnites. Solució (1,2,1)
no és un sistema d'equacions lineal. No tractarem aquest tipus de sistema.
Tipus de sistemes d'equacions
Els sistemes d'equacions, atenent al nombre de solucions que tenen, es poden classificar en:
2. Recordatori dels sistemes de dues equacions.
Veiem la classificació comentada en l'apartat anterior, en el cas de sistemes de 2 equacions, 2 incògnites:
|
Tipus de sistema Nombre de solucions |
Condició sobre els coeficients |
Gráfica |
|
Compatible determinat |
|
|
|
Una única solució |
||
|
Incompatible |
|
|
|
No té solució |
||
|
Compatible indeterminat Infinites solucions |
|
|
Recordem el 3 mètodes per resoldre un sistema de dues equacions i dues incògnites:
Substitució
a. Aïllar una incògnita d'una de les equacions
b. Substituir aquesta incògnita en l'altre equació. Obtindrem una equació amb una incògnita
c. Resoldre aquesta equació. Obtindrem el valor d'una incògnita.
d. Substituir aquest valor per obtenir el valor de l'altre incògnita
Exemple
Reducció
a. Combinar les dues equacions per obtenir una equació amb una incògnita.
b. Resoldre aquesta equació. Obtindrem el valor d'una incògnita.
c. Substituir aquest valor en una de les equacions per obtenir el valor de l'altre incògnita
Exemple
Igualació
a. Aïllar una mateixa incògnita de les dues equacions
b. Igualar les dues expressions. Obtindrem una equació amb una incògnita
c. Resoldre aquesta equació. Obtindrem el valor d'una incògnita.
d. Substituir aquest valor per obtenir el valor de l'altre incògnita
Exemple
3. Notació matricial
Donat un sistema d'equacions lineals
li associarem dues matrius:
Matriu associada al sistema (o matriu de coeficients del sistema): formada pels coeficients
Matriu ampliada: formada pels coeficients i els termes independents
Exemple
Donat el sistema d'equacions:
La seva matriu associada (o de coeficients) és:
i la matriu ampliada:
4. Transformacions elementals
Dos sistemes d'equacions són equivalents si tenen les mateixes solucions.
Transformacions elementals (per obtenir sistemes equivalents)
Si apliquem les següents transformacions a un sistema d'equacions, obtenim un sistema equivalent:
- Canviar d'ordre les equacions.
- Multiplicar (o dividir) una equació per un nombre diferent de zero. En particular: canviar tots els signes d'una equació.
- Sumar a una equació altra equació multiplicada per un nombre.
5. Mètode de Gauss
Primer de tot veiem que la resolució d'un sistema esglaonat i desprès veurem el mètode de Gauss per a la resolució de qualsevol sistema d'equacions.
Resolució d'un sistema esglaonat
Exemple de sistema esglaonat:
Veiem que començant per la última equació la resolució és immediata.
Mètode de Gauss
Donat un sistema d'equacions del qual volem trobar la solució, consisteix en obtenir un sistema esglaonat equivalent al donat fent transformacions elementals.
Si expressem el sistema matricialment, això equival a dir que fem transformacions elementals en les files per obtenir una matriu esglaonada.
Ho veurem amb un exemple.
Exemple
Considerem la matriu ampliada (formada pels coeficients i els termes independents):
Esglaonem la matriu (Està explicat en el lliurament 1 en l'apartat Esglaonar una matriu ):
Ara començant per la última fila tenim:
En la segona fil tenim:
I substituint aquest valors en la primera:
Vídeo
Exemple Resolució sistema d'equacions pel mètode de Gauss
6. Classificació d'un sistema d'equacions: Teorema de Rouché-Frobenius
Donat un sistema d'equacions lineals, sigui
M la matriu associada al sistema
M' la matriu ampliada
Teorema de Rouché-Frobenius:
Exemples:
Classifiqueu el sistema:
Esglaonem la matriu ampliada per tal de calcular els rangs de la matriu associada i de l'ampliada:
Recordem que el rang d'una matriu, un cop esglaonada, és el nombre de files no nul·les:
Classifiqueu el sistema:
Esglaonem la matriu ampliada per tal de calcular els rangs de la matriu associada i de l'ampliada:
Recordem que el rang d'una matriu, un cop esglaonada, és el nombre de files no nul·les:
Per tant:
rango 2 < 3 nombre incógnites Sistema compatible indeterminat
7. Classificació d'un sistema depenent d'un paràmetre
Classifiquem el sistema segons els valors del paràmetre k:
Ho farem per Gauss:
Si es pot, passarem l'equació que té el paràmetre a la última fila. I la 2a equació, que té primer coeficient 1, la passarem a dalt de tot. Ens quedarà:
esglaonant:
Un cop esglaonada ja podem fer la discussió dels rangs i el tipus de sistema depenent del valor de k.
En aquest cas, la discussió depén de si k-7=0 o no ja que :
8. Canvi de files o columnes en la matriu associada a un sistema d'equacions.
En la matriu associada a un sistema podem canviar l'ordre de les files sense cap repercussió (ja que l'ordre de les equacions en un sistema és irrellevant, si canviem d'ordre les equacions obtenim un sistema equivalent, és a dir, amb les mateixes solucions).
Si ens interessa també podem canviar l'ordre de les columnes però al fer això hem de pensar que estem canviat les incògnites que hi ha en cada columna. Vull dir, si per exemple tenim el sistema d'equacions:
La seva matriu associada és:
Si volem fer un intercanvi de les columnes 1 i 3 ja que pensem que d'aquesta manera ens és més fàcil esglaonar la matriu, el podem fer però tenint en compte que ara en la 1a columna tindrem els coeficients de la z, i en la 3a columna els de la x (ho
hem de recordar al acabar d'esglaonar):
ara al resoldre el sistema començant per l'última fila (recordem que amb el canvi fet en la 3a columna tenim les x), tenim:
en la 2a fila tenim:
i finalment substituint en la 1a fila:
Observació: el canvi de columnes es pot fer entre columnes de la matriu de coeficients, no amb la columna dels termes independents de la matriu ampliada.
9. Solucions d'un sistema compatible indeterminat
Farem un exemple de discussió i resolució de sistema compatible indeterminat.
El sistema és:
fixeu-vos que podem intercanviar les dues primeres files (per tal de que el primer element sigui un 1) i fins i tot podem dividir per 2 la tercera fila. D'aquesta manera tenim:
esglaonant:
Discussió (classificació):
(Teorema Rouché-Fröbenius)
rang matriu coeficients = rang matriu ampliada = 2 => compatible
rang = 2 < nombe d'incògnites = 3 => compatible indeterminat
les infinites solucions es poden expressar en funció d'1 paràmetre (ja que la diferència entre el nombre d'incògnites i el rang és 1)
Solució:
Començant per la 2a equació:
13y + z = -23
agafarem y com el paràmetre λ
13y + z = -23 => z = -13λ - 23
substituint en la 1a equació x -5y +2z =8 queda:
x - 5λ + 2(-13λ - 23) = 8 => x - 5λ - 26λ - 46 = 8 =>
x = 54 + 41λ
Per tant les solucions són
( es llegeix com "per a tot
pertanyent als reals", vol dir simplement que
pot ser qualsevol nombre real)
o bé les podem expressar com:
10. Determinats d'ordre 2 o 3
La forma més pràctica de calcular un determinant d'ordre 2 o 3 és aplicant la Regla de Sarrus.
(recordeu que només es pot calcular el determinant d'una matriu quadrada (igual nombre de files que columnes).
Determinant d'una matriu 2x2
Exemple
Determinant d'una matriu 3x3
Exemple:
Calcular el determinant de la matriu
vídeo on podreu veure més clarament com es calcula:
11. Matriu inversa
Calculem la inversa de la matriu
Ho fem de 3 maneres diferents.
(Per matrius 3x3 seria similar però quedarà una mica més llarg d'operacions)
- Utilitzant el determinant i els adjunts de la transposada.
Calcular la inversa de
Calculem el determinant
Considerem la transposada de la matriu A:
i la matriu d'adjunts de :
Per tant:
· Plantejant un sistema d'equacions:
Calcular la inversa de
Volem una matriu X tal que
És a dir:
Per tant:
· Pel mètode de Gauss-Jordan
Calcular la inversa de
De fet és el mateix que hem fet a dalt però ho expressem en forma matricial.
Es tracta de plantejar la matriu ampliada formada per la matriu i la matriu identitat. És a dir:
Hem de fer transformacions elementals fins que en la part esquerra ens quedi la matriu identitat:
Per tant:
12. Plantejament i resolució problemes
Per plantejar i resoldre un problema:
- Fer una lectura detallada de l'enunciat.
- Identificar les incògnites i les dades del problema.
- Plantejar les equacions. Rellegim l'enunciat i hem de "traduir" cada dada a una equació.
- Resoldre el sistema d'equacions plantejat (en principi, aconsellem utilitzar el sistema de Gauss).
- Interpretar les solucions en el context de l'enunciat i, si cal, descartar solucions. Comprovar que les solucions obtingudes són coherents.
Les incògnites són el preu al qual va comprar cada peça x, y i z.
De l'enunciat, traduïm cada dada a una equació
· El preu total és de 2000000.
Per comoditat podem treballar en milions, per tant:
· Els beneficis que obtindríem:
(recordem que el p% de k és )
Multipliquem per 100 :
Dividim per 5:
· Els beneficis que ha obtingut:
Multipliquem per 100:
Dividim per 5:
Tenim el sistema d'equacions:
que resolem per Gauss:
Començant per la última equació tenim:
Substituint en la segona equació:
i substituint en la primera: