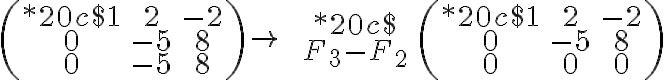Resum Matrius
| lloc: | Cursos IOC - Batxillerat |
| Curs: | Matemàtiques aplicades a les Ciències socials (autoformació IOC) |
| Llibre: | Resum Matrius |
| Imprès per: | Usuari convidat |
| Data: | dissabte, 27 d’abril 2024, 15:57 |
Descripció
Dubtes freqüents Matrius
1. Matrius
Definició
Una matriu és un conjunt d'elements disposats en files i columnes.
Diem que una matriu és d'ordre (o dimensió) nxm si té n files i m columnes. Podem escriure també (n,m)
Normalment la representem amb una lletra majúscula i els seus elements amb la mateixa lletra minúscula i amb dos subíndexs, el primer indica la fila i el segon la columna a la qual pertany l'element.
Exemples
A és una matriu 2x2
B és una matriu 2x3
C és una matriu 3x2
Igualtat de matrius
Dues matrius són iguals si tenen el mateix ordre i els elements de la mateixa fila i a la mateixa columna en les dues matrius, són iguals
2. Tipus de matrius
Segons algunes característiques de les matrius podem parlar de:
Matriu quadrada.
Són matrius d'ordre nxn, és a dir que tenen el mateix nombre de files que de columnes.
Podem dir matriu quadrada d'ordre n
Els element a11, a22,......, ann formen la diagonal principal.
Exemple:
és una matriu quadrada d'ordre n
(en negreta els elements de la diagonal principal)
Matriu fila.
Són matrius que només tenen una fila, o sigui, són de dimensió 1xm
Exemple:
Matriu columna.
Són matrius que només tenen una columna, o sigui, són de dimensió nx1
Exemple:
Matriu triangular (superior o inferior).
Són matrius quadrades en les quals tots els element situats per sota o per sobre de la diagonal són 0.
Exemple:
és triangular superior.
Matriu diagonal.
Matriu quadrada en la qual tots les elements situats a fora de la diagonal són 0
Exemple:
Matriu identitat.
Matriu diagonal en la qual tots els elements de la diagonal són 1. Se simbolitza per I.
Exemple:
Matriu nul·la o matriu zero.
Tots els seus elements són 0.
Exemple:
Matriu transposada.
La matriu transposada At d'una matriu A és la que s'obté intercanviant les seves files per les seves columnes.
Podem escriure At o AT o tA
Si la matriu A és d'ordre (n,k), la matriu transposada At és d'ordre (k,n)
Exemple
A és d'ordre (2,3), At és d'ordre (3,2)
Matriu simètrica.
Una matriu A diem que és simètrica si és igual a la seva transposada.
A és simètrica si A = At
Matriu esglaonada.
Són matriu en què tots els element per sota de la "diagonal" són 0 (posem "diagonal" ja que en propietat només es pot parlar de diagonal en matrius quadrades però en aquest ho fem extensiu a matrius no quadrades.
Exemple:
3. Operacions amb matrius
Suma de matrius.Per tal que dues matrius es puguin sumar han de ser del mateix ordre.
Donades dues matrius del mateix ordre , la matriu suma de A i B és la que s'obté de la suma de cada terme de A amb el corresponent de B:
Exemple
Observació:
La resta de dos matrius la considerem com:
sent la matriu oposada a la B, que és la matriu B canviats de signe tots els seus elements
Producte d'un nombre per una matriu.
Es multiplica cada element de la matriu pel nombre.
Exemple
Producte de matrius.
La condició per tal que dues matrius es puguin multiplicar és que el nombre de columnes de la primera matriu sigui igual al nombre de files de la segona matriu.
O sigui, per poder fer el producte A·B, la condició és:
nombre de columnes de A = nombre files de B
I llavors:
A és de dimensió m x k
B és de dimensió k x n
=>
A·B és de dimensió m x n
Per exemple, si multipliquem una matriu A 3x3 per una B 3x2,
el producte A·B es pot fer i és una matriu de dimensió 3x2 (el producte B·A no seria possible).
Important: El producte de matrius no és commutatiu.
Obtenció de la matriu producte.
a)
Primer veiem el producte d'una matriu fila F1 per una matriu columna C1
Exemple
b) Cas general: producte d'una matriu A d'ordre (n,m) per una matriu B d'ordre (m,k)
Exemple 1
A ordre (1,3), B ordre (3,2) => A·B ordre (1,2)
Exemple 2
A ordre (2,3), B ordre (3,2) => A·B ordre (2,2)
Exemple 3
A ordre (3,3), B ordre (3,2) => A·B ordre (3,2)
Observació: En els exemples 1 i 3 no és possible fer el producte B·A
Potència d'una matriu.
Expressem com a el producte de la matriu A per ella mateixa n vegades. O sigui:
Observacions:
- Per poder fer , la matriu A ha de ser quadrada.
- Per calcular A3 primer calcularem A2 i desprès podem fer o
Vídeo producte de matrius
4. Transformacions elementals
Són les operacions que podem fer amb les files o columnes d'una matriu mantenen el rang:
- Intercanviar dues files,o sigui, canviar l'ordre de les files. Per exemple
- Multiplicar una fila per un nombre diferent de zero. Per exemple
En particular podem canviar una fila de signe. Per exemple
- Sumar a una fila altra fila multiplicada per un nombre . Per exemple
(aquestes operacions es poden fer també amb les columnes).
Si a una matriu li apliquem transformacions elementals obtenim una matriu equivalent.
Dues matrius equivalents tenen el mateix rang.
Exemples de transformacions elementals sobre una matriu:
Observació: entre pas i pas dels esglaonaments posem el símbol
Podem posar , ; , res, ... però mai el símbol d'igualtat = ja que les matrius no són iguals.
5. Esglaonar una matriu
Esglaonament d'una matriu fent transformacions elementals.
Exemple 1
Esglaonar la matriu
Sempre ens facilita els càlculs si el primer element de la matriu és "1", per això podem canviar l'ordre de les files
El rang d'aquesta matriu és 2
Exemple 2
Esglaonar la matriu
(En aquest cas no tenim cap "1" en la primera columna
El rang d'aquesta matriu és 3 ja que en la matriu esglaonada (zeros sota la diagonal), ens queden 3 files no nul·les.
Exemple 3
Esglaonar la matriu
Veurem aquest cas en què l'esglaonament ens queda una mica diferent. Ho resolem així:
En aquest cas el que fem és que intercanviem les dues últimes files:
I veiem que la matriu està ja esglaonada.
El rang d'aquesta matriu és 3 ja que en la matriu esglaonada (zeros sota la diagonal), ens queden 3 files no nul·les.
Vídeo esglaonar matriu:
6. Rang d'una matriu
Definició
El rang d'una matriu és el nombre de files (o columnes) independents que té la matriu.
I que vol dir que les files siguin independents?
Si, per exemple, tenim la matriu
Veiem que la fila 3 la podem obtenir combinant les altres dues files:
F3 = 3F1 - F2
Es diu que la fila 3 és combinació lineal de la fila 1 i la fila 2. O també es diu que la fila 2 és depenent de la 1 i la 2.
Llavors el rang d'aquesta matriu serà 2 ja que hi ha 2 files independents (observem que la fila 2 no la podem obtenir com la fila 1 multiplicada per un nombre, per tant la fila 1 i la 2 són independents) .
A vegades es pot veure a ull, però normalment no és tan obvi. Veiem com fem el càlcul.
Càlcul del rang d'una matriu.
1) Si la matriu és esglaonada.
El rang d'una matriu esglaonada és el nombre de files no nul·les de la matriu.
Exemples
2) Si la matriu no és esglaonada.
Fem transformacions elementals per esglaonar la matriu. D'aquesta manera el rang de la matriu serà el mateix que el de la matriu esglaonada que s'obté.
Heu de mirar els subapartats:
- Transformacions elementals
- Esglaonar una matriu
Exemple:
Calculeu el rang de la matriu
Esglaonem la matriu fem transformacions elementals:
Per tant, com que queden dues files no nul·les, el rang d'aquesta matriu esglaonada és 2.
rang A = 2
Observació: entre pas i pas dels esglaonaments he posat el símbol
Podem posar , ; , res, però
mai el símbol d'igualtat = ja que les matrius no són iguals.
Vídeo:
7. Error freqüent (i greu) en el càlcul de rangs
Quan es calcula el rang d'una matriu sovint es comet un error greu. És referent a les transformacions elementals en una matriu. Recordeu que les transformacions elementals conserven el rang de la matriu. L'error és fer això:
Això no és correcte perquè els passos s'han de fer d'un en un. És a dir, si en la segona fila fem F2-F3, ens quedarà:
I encara que ara en aquesta nova matriu féssim la tercera fila menys la segona, no se'ns anul·laria. Per tant el que s'ha de fer és esglaonar la matriu pas a pas.És a dir, quan tenim
les dues primeres files les deixem i ara "fem un zero" combinant la tercera amb la 2a:
i, per tant, el rang de la matriu és 2.
De la mateixa manera no és correcte, per exemple, aquest pas ( o alguna cosa similar):
(si això es pogués fer sempre podríem arribar a rang 1 !)
8. Sistemes matricials
Amb matrius treballem de manera semblant que amb números:
Exemples:
fixeu-vos que -B s'btindrà canviant de signe tots els element de B
I per exemple, 5A és la matriu que s'obté de multiplicar tots els elements per 5
En aquest exemples per aïllar la matriu X simplement fem:
Cas o
Aquest cas és el més interessant i s'ha de tenir cura com es resol. Ho tractem amb detall.
Fixeu-vos que en matrius no tenim l'operació quocient de matrius. No podem fer A/B
Farem un exemple per explicar dues maneres diferents de fer-ho.
Exemple
Mètode 1: Plantejant el sistema.
Primer de tot hem de pensar de quin ordre ha de ser la matriu X que busquem:
A és 2x2, B és 2x3 → X és 2x3
2 files per tal que es pugui multiplicar per A que té 2 columnes
3 columnes ja que ha de donar una matriu de 3 columnes
Per tant, la matriu X serà de la forma:
El sistema que es planteja és:
Multiplicant tenim:
Igualem element a element i plantegem 3 sistemes d'equacions.
Resolent aquests sistemes trobem que
a=-1 c=4 e=1
Per tant:
· Métode 2: Amb la inversa de la matriu A (Si la matriu A és invertible)
Primer de tot fixeu-vos en la diferència de tenir o
En aquest cas multipliquem per l'esquerra (això és important!) tota l'equació per la inversa de A:
A-1·A·X = A-1·B
Com que A-1·A= I (matriu identitat):
X = A-1·B
En aquest cas multipliquem per la dreta tota l'equació per la inversa de A
XA·A-1= B·A-1
Com que A·A-1= I (matriu identitat):
X = B·A-1
En el cas de l'exemple volem la matriu X tal que A·X=B
Per tant:
Ara necessitem A-1 (l'hem calculat en Matriu inversa)
Per tant:
Observació: Si la matriu A no té inversa obligatòriament ho hem de fer plantejant un sistema d'equacions.
9. Inversa de matrius
Definició
Donada una matriu quadrada A, la seva matriu inversa A-1, si existeix, és la matriu que compleix:
on I és la matriu Identitat.
En aquest bloc ens limitarem al càlcul de matrius inverses d'ordre 2x2.
Ho podem fer de dues maneres. Ho veurem amb un exemple.
Exemple
Calcular la inversa de la matriu
· Càlcul de la matriu inversa a partir de la definició.
Plantegem un sistema d'equacions, ja que volem una matriu X tal que
És a dir:
Per tant:
· Càlcul de la matriu inversa pel mètode de Gauss-Jordan
De fet és el mateix que hem fet a dalt però ho expressem en forma matricial:
Es tracta de palntejar la matriu ampliada:
Hem de fer transformacions elementals fins que en la part esquerra ens quedi la matriu identitat:
Per tant:
Observacions:
- El procediment per trobar la inversa de matrius quadrades de qualsevol ordre major és el mateix. Simplement pot sortir més llarg de càlculs.
- No sempre existeix la matriu inversa d'una matriu.
Fixeu-vos que, amb el primer mètode, el sistema que plantegem podria ser que no tingués solució.
O amb el segon mètode podria ser que no poguéssim obtenir la matriu identitat a l'esquerra.
La condició perquè una mateix quadrada tingui inversa és que el seu determinant no sigui 0 però això ho veurem en el següent lliurament.
- Hi ha un tercer mètode però utilitza els determinants (que s'estudien en el lliurament 2).
10. Inversa de matrius
Definició
Donada una matriu quadrada A, la seva matriu inversa A-1, si existeix, és la matriu que compleix:
on I és la matriu Identitat.
En aquest bloc ens limitarem al càlcul de matrius inverses d'ordre 2x2.
Ho podem fer de dues maneres. Ho veurem amb un exemple.
Exemple
Calcular la inversa de la matriu
· Càlcul de la matriu inversa a partir de la definició.
Plantegem un sistema d'equacions, ja que volem una matriu X tal que
És a dir:
Per tant:
· Càlcul de la matriu inversa pel mètode de Gauss-Jordan
De fet és el mateix que hem fet a dalt però ho expressem en forma matricial:
Es tracta de palntejar la matriu ampliada:
Hem de fer transformacions elementals fins que en la part esquerra ens quedi la matriu identitat:
Per tant:
Observacions:
- El procediment per trobar la inversa de matrius quadrades de qualsevol ordre major és el mateix. Simplement pot sortir més llarg de càlculs.
- No sempre existeix la matriu inversa d'una matriu.
Fixeu-vos que, amb el primer mètode, el sistema que plantegem podria ser que no tingués solució.
O amb el segon mètode podria ser que no poguéssim obtenir la matriu identitat a l'esquerra.
La condició perquè una mateix quadrada tingui inversa és que el seu determinant no sigui 0 però això ho veurem en el següent lliurament.
- Hi ha un tercer mètode però utilitza els determinants (que s'estudien en el lliurament 2).
11. Problemes interessants PAU
Donades les matrius
a) Trobeu la matriu
b) Justifiqueu si és cert que
En aquest exercici no hi ha cap dificultat especial però, un cop fet l'apartat a), se us acudeix de com fer l'apartat b) sense calcular explícitament ?.
---------------------------------------------------------------------------------------------------------------
Sigui A una matriu quadrada que compleix que A3= I, en què I és la matriu identitat,
Demostreu que la matriu A té inversa i que
-------------------------------------------------------------------------------------------------------------------------------------------
Aquest dos problemes següents són interessants ja què no són el típic problema de plantejament de 3 equacions i 3 incògnites.
Podeu buscar el solucionari en Enunciats i resolució d'exàmens PAU
------------------------------------------------------------------------------------------------------------------
2016 Sèrie 5 juny
Dues famílies van a una cafeteria. La primera família pren 1 refresc, 3 cafès i 7 magdalenes, i paga un total d'11,75 €. La segona família demana 1 refresc, 4 cafès i 10 magdalenes i paga per tot plegat 15,5 €.
a) Digueu, raonadament, si és possible saber el preu d'un cafè, el d'un refresc i el d'una magdalena.
b) Calculeu quant ha de pagar una família que prengui un refresc, un cafè i una magdalena.
--------------------------------------------------------------------------------------------------------------------
2018 Sèrie 1 juny
En Pol va quedar ahir amb uns amics en un bar i van prendre 4 refrescs, 3 entrepans i 5 boles de gelat. Tot plegat les va costar 19,50 €. Dies enrere, havia anat al mateix bar amb el seu cosí Martí, i per 2 refrescs, 1 entrepà i 2 boles de gelat havien pagat 8,10 €. En aquest bar tots els refrescs valen el mateix, tots els entrepans tenen el mateix preu i les boles de gelat també a preu únic.
a) Avui en Pol hi ha tornat amb uns altres amics i han pres 6 refrescs, 5 entrepans i 8 boles de gelat. Expliqueu raonadament quant han pagat en total.
b) Si 1 refresc, 1 entrepà i 1 bola de gelat costen 5,10 € quant val el refresc, l'entrepà, i la bola de gelat separadament?