R1.1. Els nombres Racionals
| lloc: | INS Reguissol |
| Curs: | Matemàtiques 3r ESO |
| Llibre: | R1.1. Els nombres Racionals |
| Imprès per: | Usuari convidat |
| Data: | dimecres, 26 de juny 2024, 17:28 |
Descripció
Llibre amb els continguts del tema.
1. Recordem
Els nombres Enters
En el conjunt dels Enters tenim els nombres positius (nombres Naturals), els nombres negatius (que ens són útils per temperatures negatives, soterranis, deutes,...) i el zero.
![]()
[Drets de la imatge: Enricbraso / CC BY-SA]
Cal recordar.
Nombre positiu: va precedit del signe + i és major de zero.
Nombre negatiu: precedit del signe- i menor de zero.
Valor absolut: és el nombre que obtenim si suprimim el signe d'un nombre enter
Oposat d'un nombre: és el que obtenim canviant el signe del nombre inicial
Ordenats: els negatius són menors que zero i que els positius tal com es veu en la imatge de dalt.
Suma: Si tenen igual signe se sumen i posen el signe comú; si tenen signe diferent es resten i posem el signe del més gran.
Resta: sumem al primer l'oposat del segon.
Regla dels signes (producte i divisió): dos signes iguals el resultat és positiu, dos signes diferents el resultat és negatiu.
+ · + = +
− · − = +
+ · − = −
− · + = −
mcm (mínim comú múltiple)
El mínim comú múltiple entre dos o més nombres és el més petit (mínim) de tots els múltiples comuns entre els nombres. Fixem-nos amb les paraules.
Per trobar-lo cal descompondre cada nombre en els seus factors primers i el mcm són els factors repetits i no repetits al màxim exponent. Veiem un exemple.
Trobem mcm de 12, 10 i 15,
1r: Descomponem: 12 = 22· 3; 10 = 2 · 5; 15 = 3 · 5
2n: mcm = 22· 3 · 5 = 60
Una altra forma per trobar-lo en el cas de pocs nombres i relativament petits és la següent:
Prenem el més gran dels nombres i mirem si es pot dividir de forma exacta pels altres dos. Si és possible, el més gran és el mcm; si no, en fem el doble del gran i ho tornem a mirar. Si és possible, és el mcm, si no, en fem el triple i ho tornem a mirar i així, fins a trobar el mcm.
Pel cas anterior:
El nombre més gran 15 no és divisible per 12 ni 10. En fem el doble, 15 · 2 = 30; 30 no és divisible per 12. En fem el triple, 15 · 3 = 45, tampoc; multipliquem per 4, 15 · 4 = 60, ara ja és divisible per 12 i per 10. Llavors: mcm = 60.
2. Les fraccions
Les fraccions
A vegades ens trobem en situacions que cal que dividim un objecte en diverses parts, n'haurem de fer la meitat, la tercera part, una dècima part,... Per tant, estem fraccionant la unitat i, a més, podem agafar-ne més d'una de les parts.
Llavors, tenim el concepte de fracció. Exemples de fraccions són: una meitat:  , dos terços:
, dos terços:  , tres dècimes:
, tres dècimes:  ,...
,...

En la imatge[1], en taronja un quart  i en verd tres quarts
i en verd tres quarts  .
.
 .
.
Si el numerador és més petit que el denominador, com en els exemples anteriors, diem que la fracció és pròpia. En cas contrari diem que és impròpia i, llavors, necessitem més d'una unitat.
Exemple de fracció impròpia és:  =
=  +
+  = 1 +
= 1 +  , necessitem dos quadrats per poder-la representar seguint aquesta imatge[2].
, necessitem dos quadrats per poder-la representar seguint aquesta imatge[2].
La fracció impròpia la podem escriure també en format de nombre mixt com: 1  .
.
1 Autor: canuoislupusarctos sota llicència
Creative Commons Attribution-Share Alike 3.0 Unported
2 Imatge de Jaume Bartolí Guillemat sota llicència CC BY-NC-SA 3.0
Simplificació de fraccions
Si numerador i denominador d'una fracció es poden dividir per un mateix nombre podem simplificar la fracció, convertint-la en una fracció equivalent, i el seu valor no canvia.
Diem que dues fraccions són equivalents si una s'obté per simplificació de l'altra o, equivalentment,  i
i  són equivalents si a · d = b · c.
són equivalents si a · d = b · c.
El procés de simplificació pot seguir fins que arribem a la fracció irreductible, la qual ja no es pot simplificar més.
Exemple:  =
=  =
=  . En el primer pas hem dividit numerador i denominador per 2 i en el segon per 3. La fracció irreductible és
. En el primer pas hem dividit numerador i denominador per 2 i en el segon per 3. La fracció irreductible és  .
.
La fracció com a operador
Podem considerar una fracció com un operador quan actua sobre un altre nombre. Fixem-nos amb l'exemple:
Quants minuts són els  d'una hora?
d'una hora?
Veiem que el numerador multiplica el nombre i el denominador divideix al resultat anterior.
Comparació i ordenació
En general, comparar dues fraccions no és immediat. Si les dues fraccions tenen igual denominador, llavors només cal comparar els numeradors per poder dir quina és més gran. Per exemple:  >
>  .
.
Però si els denominadors són diferents cal trobar fraccions equivalents a les inicials que tinguin el mateix denominador i, llavors, ja les podrem comparar. Per exemple:  i
i  les transformem en
les transformem en  i
i  ; ara ja les podem comparar
; ara ja les podem comparar  >
>  , per tant
, per tant  >
>  .
.
Com que podem comparar les fraccions també les podem ordenar de més petita a més gran.
Representació gràfica en la recta
Per representar una fracció sobre la recta cal fer tantes divisions entre cada dues unitats de la recta com ens diu el denominador, i la fracció estarà en la divisió apropiada començant a comptar des del zero.


Imatges de Jaume Bartolí Guillemat sota llicència
CC BY-NC-SA 3.0
Els Nombres Racionals
Fins ara teníem el conjunt dels nombres Naturals  que en serveixen per comptar objectes. Si els hi afegim els negatius tenim el conjunt dels Enters
que en serveixen per comptar objectes. Si els hi afegim els negatius tenim el conjunt dels Enters  amb totes les possibilitats que ens ofereixen.
amb totes les possibilitats que ens ofereixen.
Ara, als Enters els hi afegim les fraccions. Això ens dona un conjunt nou anomenat el conjunt dels nombres Racionals  que inclou els enters i les
fraccions.
que inclou els enters i les
fraccions.
Els Nombres Irracionals i els Reals
Però els nombres Racionals no exhaureixen tots els nombres decimals que existeixen. Per exemple, el nombre π, les arrels no exactes  ,
,  ,
,  ,... no es poden expressar com fraccions.
,... no es poden expressar com fraccions.
I encara n'hi ha més de nombres com aquests 1,23456789101112.....; 1,101001000100001.... O d'altres que pots construir.
Tots aquests nombres que no es poden expressar com una fracció s'anomenen Nombres Irracionals.
Si unim els nombres Racionals i els Irracionals tenim un conjunt nou anomenat Nombres Reals. Aquest ja engloba tots els nombres.
Activitat Sobre aquests continguts podeu fer les activitats A1.1. Conceptes de fraccions i A1.2. Fraccions sobre la recta.
3. Operacions amb fraccions
Sumar i restar fraccions
Sumar o restar fraccions que tenen el mateix denominador és senzill, només cal sumar o restar els numeradors. Per exemple:
Si tenen denominadors diferents cal, primer, convertir-les en les seves fraccions equivalents de forma que totes tinguin el mateix denominador comú. Per tant, trobem el mcm dels denominadors que serà el nou denominador:
en aquest cas mcm (denominadors) = 12. Llavors, transformem cada fracció en la seva equivalent amb denominador 12 dividint 12 entre el denominador actual i multiplicant pel numerador. Així:
En cas que el resultat es pugui simplificar així ho farem trobant la fracció irreductible.
Veiem un vídeo explicatiu:
Vídeo d'Antoni Tornero Cobos. Disponible en aquest canal.
Una forma equivalent de sumar i restar fraccions sense fer servir el mcm és operant les fraccions de dos en dos i multiplicant cada fracció pel denominador de l'altra fracció. Vegem-ho:
Multipliquem la primera fracció per 6 i la segona per 4:
Llavors:
Simplifiquem:
Ara, acabant amb la simplificació del resultat:
Multiplicar fraccions
Per multiplicar dues fraccions cal multiplicar per separat els numeradors i els denominadors. Així:
simplificant el resultat.
Dividir fraccions
Per dividir dues fraccions multipliquem la primera per la inversa de la segona. Equivalentment, diem que les fraccions es multipliquen en creu. Així:
simplificant el resultat.
Potència d'una fracció
Per fer una potència d'una fracció cal fer la mateixa potència del numerador i del denominador. Així:
Parèntesi i prioritat d'operacions
En expressions complexes on tinguem diverses operacions i parèntesi cal seguir el següent criteri a l'hora d'operar:
- Els càlculs de dins els parèntesi.
- Potències.
- Productes i divisions.
- Sumes i restes.
Podem veure un exemple en aquest vídeo:
Vídeo d'Antoni Tornero Cobos. Disponible en aquest canal.
Activitat Sobre aquests continguts podeu fer l'activitat A1.3. Operacions amb fraccions.
4. Nombres decimals
Fraccions i Decimals
 Una fracció, de
fet, representa també una divisió entre dos nombres. Si fem aquesta divisió obtindrem un nombre decimal o un nombre enter que són equivalents a la fracció.
Una fracció, de
fet, representa també una divisió entre dos nombres. Si fem aquesta divisió obtindrem un nombre decimal o un nombre enter que són equivalents a la fracció.
Per exemple:  = 1,25;
= 1,25; 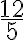 = 2,2;
= 2,2;  = 3.
= 3.
Imatge lliure de Piqsels
Tipus de decimals
A partir de les fraccions podem tenir tres tipus diferents de decimals:
Decimals exactes: són els que tenen un nombre finit de xifres decimals. Exemples: 1,25; 6,742; 3,8495.
Decimals periòdics purs: són els decimals que tenen un nombre infinit de xifres decimals però que totes es repeteixen. Exemples: 2,555555..... =  ; 4,62..... =
; 4,62..... =  ; 56,178..... =
; 56,178..... =
 . El grup de nombres decimals que es repeteix s'anomena període.
. El grup de nombres decimals que es repeteix s'anomena període.
Decimals periòdics mixtos: són els decimals que tenen infinites xifres decimals amb unes quantes al començament que no es repeteixen i altres, darrere, que sí. Exemple: 2,3555555..... =  ; 4,6212121..... =
; 4,6212121..... =  ; 56,12787878..... =
; 56,12787878..... =  . Igual que abans, el grup de nombres decimals que es repeteix s'anomena període.
. Igual que abans, el grup de nombres decimals que es repeteix s'anomena període.
Operacions de decimals
Farem aquí només un petit recordatori de les idees bàsiques de les operacions amb decimals que ja has vist en cursos anteriors.
Sumar i Restar
Cal situar ordenadament els nombres segons la coma decimal. Per exemple,
| 3 | 4, | 5 |
2 | ||
| + | 9, | 3 | 6 | 4 | |
| 4 | 3, | 8 | 8 | 4 |
Multiplicar
Multipliquem els dos nombres sense considerar la coma decimal en cap d'ells. Llavors, contem quants decimals contenen en total els dos nombres i situem la coma decimal en el resultat de forma que tingui tants decimals com hem comptat.
Dividir
A l'hora de dividir cal, primer, multiplicar els dos nombres per la potència necessària de 10 per eliminar els decimals del divisor. Llavors, dividim de la forma habitual tenint en compte que quan usem el primer decimal del dividend cal posar la coma
decimal en el quocient.
Aproximacions
A vegades podem tenir nombres decimals amb més decimals dels que són necessaris per al context en què treballem. Per exemple, si estem parlant de preus, no té gaire sentit treballar amb més de dos decimals donat que els euros poden tenir fins a cèntims.
Per aproximar un decimal a un nombre concret de xifres decimals ho podem fer de dues formes:
Truncament: en aquest cas simplement eliminem les xifres decimals que no interessen. Així, aproximem el nombre 4,736 a dos decimals amb 4,73; o, 7,832 amb 7,83.
Arrodoniment: ara ens fixem en el primer decimal eliminat, si és major o igual a 5 augmentem en un el decimal anterior, i si és menor, no el modifiquem. Així, 4,736 ara s'aproxima per 4,74, i 7,832 per 7,83.
Si el valor aproximat és major que el nombre inicial diem que l'aproximació és per excés. Si el valor aproximat és menor, diem que és per defecte. Llavors, 4,736 →4,74 és per excés i 7,832 per 7,83 és per defecte.
Activitat Sobre aquests continguts podeu fer part de l'activitat A1.4. Nombres decimals.
5. Conversió fracció-decimal
Pas de fracció a decimal
Com s'ha comentat en l'apartat anterior, per trobar el nombre decimal associat a una fracció cal fer la divisió que aquesta representa:
Pas de decimal a fracció
Per trobar la fracció que cadascun del tipus de decimals que hem vist a l'apartat anterior procedirem de forma diferent segons el tipus de decimal.
Decimals exactes.
La fracció tindrà en el numerador el nombre sense la coma decimal i en el denominador la potència de 10 amb exponent el nombre de xifres decimals.
Decimals periòdics purs.
Procedim com segueix amb el nombre  :
:
n = 2,55555...; multipliquem per la potència de 10 segons el nombre de xifres del període: 10n =25,55555...
Restem les dues expressions 10n - n = 23 → 9n = 23 →  =
=  .
.
Decimals periòdics mixtos.
Seguim aquests passos amb el nombre  :
:
n = 2,854545454...; multipliquem per 10 per convertir-lo en periòdic pur: 10n = 28,54545454...
Multipliquem, ara per la potència de 10 segons el nombre de xifres del període (100):
1000n = 2854,545454...
Restem les dues expressions 1000n - 10n = 2854,545454... - 28,545454... = 2854 - 28 = 2826
Activitat Sobre aquests continguts podeu fer part de l'activitat A1.4. Nombres decimals.
6. Percentatges
Fracció i percentatge
Podem considerar que un percentatge és equivalent a una fracció amb el denominador igual a 100. Així, tenim 60% = 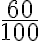 , i si simplifiquem la fracció 60% =
, i si simplifiquem la fracció 60% = 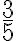 .
.
Càlcul de percentatges
Amb el raonament anterior el percentatge d'una quantitat és aplicar la fracció a la quantitat com operador. Així:
Augments i disminucions percentuals
 En molts casos cal que afegim a una quantitat
un determinat percentatge (increments de preu, IVA, creixements de població...). De forma equivalent, en altres casos haurem de treure un percentatge a una quantitat (descomptes, decreixements...)
En molts casos cal que afegim a una quantitat
un determinat percentatge (increments de preu, IVA, creixements de població...). De forma equivalent, en altres casos haurem de treure un percentatge a una quantitat (descomptes, decreixements...)
Exemple d'afegir:
A un determinat article de preu brut 500 € li hem d'afegir l'IVA del 20%. Quin és el preu final?
Resolució, calculem el 20% de 500: 20· 500 : 100 = 100 € i el sumem a la quantitat inicial: 500 + 100 = 600. El preu final és de 600 €.
Exemple de treure:
Sobre un determinat article de preu final 200 € ens fan un descompte del 15%. Quin és el preu a pagar?
Resolució, calculem el 15% de 200: 15 · 200 : 100 = 30 € i el restem a la quantitat inicial: 200 - 30 = 170. El preu final és de 170 €.
Imatge de Jaume Bartolí Guillemat sota llicència
CC BY-NC-SA 3.0
Equivalentment, els càlculs anteriors es poden fer amb el que anomenem tant per u. Així, un 20% és igual a 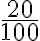 = 0,20. Per tant, calcular el 20% d'una quantitat es pot fer multiplicant per 0,20.
= 0,20. Per tant, calcular el 20% d'una quantitat es pot fer multiplicant per 0,20.
Llavors, si volem calcular un increment percentual, tindrem el 100% 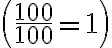 de la quantitat més el tant per u anterior, o sigui, 1 + 0,20 = 1,20. Multiplicarem la quantitat per 1,20. En el cas anterior, 500 · 1,20
= 600 €.
de la quantitat més el tant per u anterior, o sigui, 1 + 0,20 = 1,20. Multiplicarem la quantitat per 1,20. En el cas anterior, 500 · 1,20
= 600 €.
En el cas del descompte anterior, farem 15% = 0,15. Com que és un descompte restarem 1 - 0,15 = 0,85. Llavors, 200 · 0,85 = 170 €.
Activitat Sobre aquests continguts podeu fer l'activitat A1.5. Càlcul de percentatges i la que us correspongui de les A1.6.
7. La Calculadora
Fraccions en la calculadora
Podem operar les fraccions en la calculadora científica fent ús de les tecles següents (dependrà del model de la calculadora, tindrem un o altra tecla):
 |
|---|
En el primer cas cal prémer aquesta tecla entre numerador i denominador.
En el segon cas cal prémer primer la tecla i omplir la fracció en pantalla movent-nos amb la tecla avall o amunt (tecles amb fletxes).
En els dos casos cal treballar conjuntament amb la tecla Shift  si obtenim fraccions impròpies.
si obtenim fraccions impròpies.
Exemples:
Simplificar. Posem la fracció  i premem la tecla igual i obtindrem la fracció irreductible.
i premem la tecla igual i obtindrem la fracció irreductible.
Operacions. Introduint les fraccions com s'ha comentat anteriorment podem fer les operacions amb fraccions. En cas que siguin necessari també podem utilitzar les tecles de parèntesi![]() .
.
Decimals en la calculadora
Fent ús de la tecla del punt decimal ![]() podem operar amb nombres decimals de forma molt fàcil. Recordem que la calculadora treballa amb la notació anglosaxona pel separador decimal, per això no ens apareix la coma decimal sinó el punt. Així i tot, la majoria
de calculadores es poden configurar perquè mostrin en pantalla la coma decimal.
podem operar amb nombres decimals de forma molt fàcil. Recordem que la calculadora treballa amb la notació anglosaxona pel separador decimal, per això no ens apareix la coma decimal sinó el punt. Així i tot, la majoria
de calculadores es poden configurar perquè mostrin en pantalla la coma decimal.
Imatges extretes de fotos de calculadores científiques de Rafael Javier i kostkarubika005 a Pixabay



































